2.1.1 向量的概念 课件(28张PPT)
文档属性
| 名称 | 2.1.1 向量的概念 课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 709.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 09:23:20 | ||
图片预览



文档简介
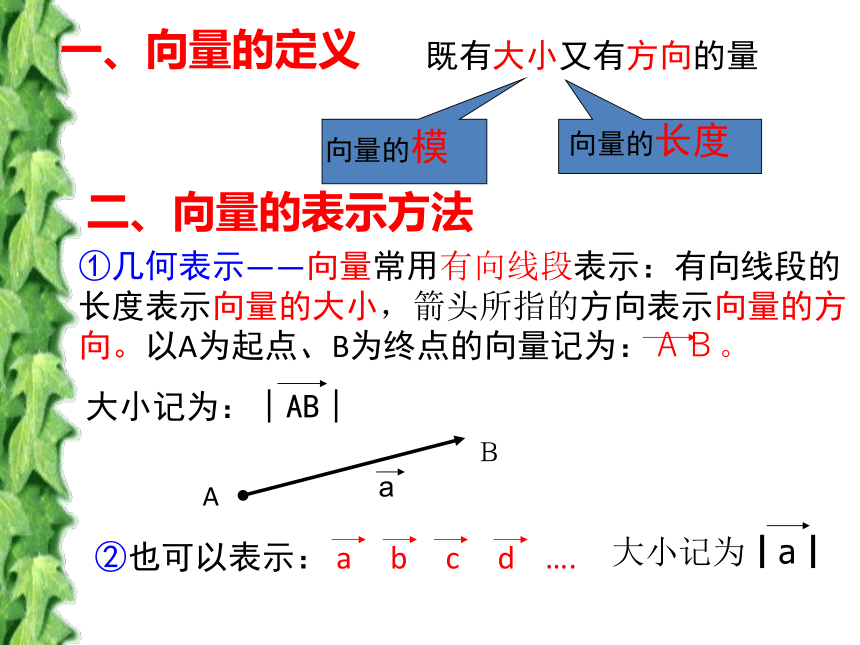
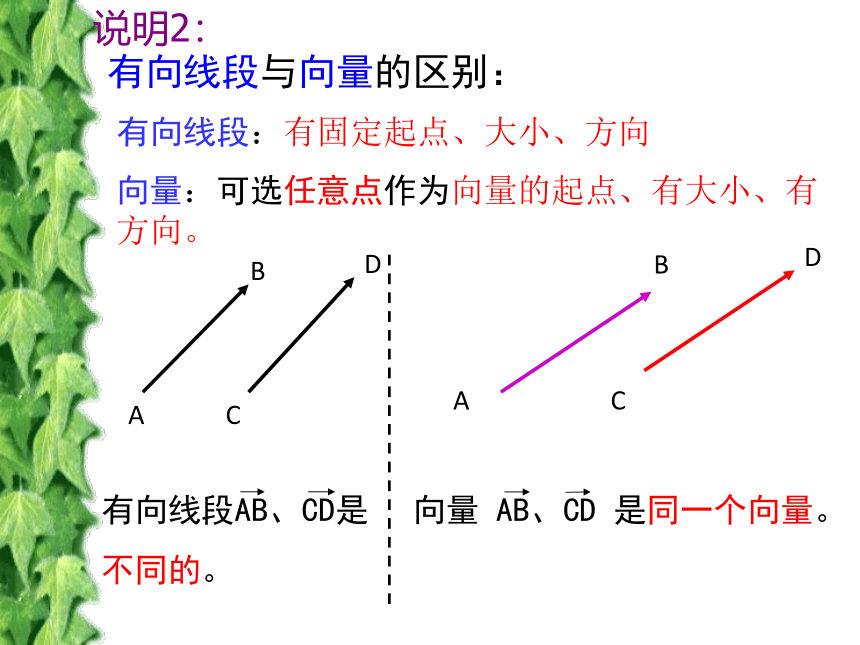
课件28张PPT。2.1向量的线性运算2.1.1向量的概念请问:金钱豹 能追上小狗吗?为什么?问 题 情 境:金钱豹以5m/s的速度追赶一只以2m/s逃跑的小狗…… 由于大陆和台湾没有直航,因此2006年前,春节探亲,乘飞机要先从台北到香港,再从香港到上海,这里发生了两次位移。 台北香港上海问 题 情 境:位移和距离这两个量有什么不同?F=20NV =20km/h (2)(3)都是有大小和方向的量m=20kg(1)(2)(3)观察下述三个量有什么区别?向量的概念二、向量的表示方法一、向量的定义既有大小又有方向的量我们现在研究的向量,与起点无关,用有向线段表示向量时,起点可以取任意位置。所以数学中的向量也叫 自由向量如图:他们都表示同一个向量。不是,温度只有大小,没有方向。不是,方向不同说明1:小试牛刀有向线段与向量的区别:有向线段:有固定起点、大小、方向向量:可选任意点作为向量的起点、有大小、有方向。说明2:单位向量大小为1,方向
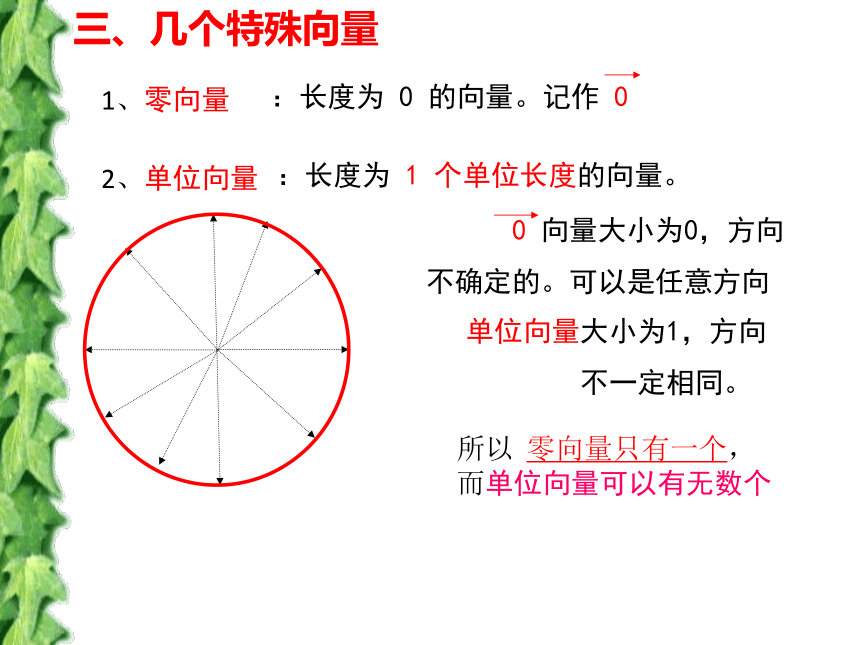
不一定相同。所以 零向量只有一个,而单位向量可以有无数个:长度为 1 个单位长度的向量。三、几个特殊向量3.相等向量的定义:长度相等且方向相同的向量相反向量的定义:4.平行向量、共线向量的定义:基线平行或重合的向量叫做平行向量或共线向量。两向量的平行与平面几何里两线段的平行有什么区别?我们规定零向量与任一向量平行通过有向线段 的直线叫向量 的基线。即共线向量或平行向量的方向相同或相反。例1:已知O为正六边形ABCDEF的中心,
在图中所标出的向量中:解:分别以图中的格点为起点和终点作向量,练习一
1、单位向量是否一定相等?
2、单位向量的大小是否一定相等?BACK不一定一定练习二
1、平行向量是否一定方向相同?
2、不相等的向量一定不平行吗?BACK不一定不一定BACK练习三
1、与零向量相等的向量一定是什么向量?
2、与任意向量都平行的向量是什么向量?零向量零向量练习四
1、若两个向量在同一直线上,则这两个
向量是什么向量?
2、共线向量一定在一条直线上吗?共线向量 或者说平行向量不一定BACK练习五
在质量、重力、速度、身高、面积、体积这些量中,哪些是数量?哪些是向量?数量有:质量、身高、面积、体积向量有:重力、速度BACK在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终
点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等。正确的有:(4)练习六BACK练习七
1.设O为正△ABC的中心,则向量AO,BO,CO是 ( )
A.相等向量 B.模相等的向量
C.共线向量 D.共起点的向量
BABCOBACK练习八
命题:“│a│=│b│”成立,则“ a = b ”一定成
立×BACK练习九
1.已知a、b为不共线的非零向量,且
存在向量 c,使 c ∥ a, c ∥ b, 则
c =____BACK练习十
1.与非零向量 a 平行的向量中,
不相等的单位向量有_____个.2 BACK练习十一 如图,EF是△ABC的中位线,AD是BC 边上的中线,在以A、B、C、D、E、F为端点的有向线
段表示的向量中请分别写出
(1)与向量CD共线的向量有___个,
分别是______________________;
(2)与向量DF的模一定相等的向
量有__个,分别是_________________;
(3)与向量DE相等的向量有__个,
分别是___________。 ABCDEF752BACK如图,D、E、F分别是△ABC各边上的中点,四边形BCMF是平行四边形,请分别写出:
(1)与ED相等的向量;
(2)与ED共线的向量;
(3)与FE相等的向量;
(4)与FE共线的向量。ABCDFEM(1) 3个(2) 9个(3) 3个(4) 11个练习十二BACK课堂小结 向量最初被应用于物理学,被称为矢量.很多物理量,如力、速度、位移、电场强度、磁场强度等都是向量。
大约公元前350年,古希腊著名学者亚里士多德就知道了力可以表示为向量.向量一词来自力学、解析几何中的有向线段。
最先使用有向线段表示向量的是英国大科学家牛顿。课堂小结向量及向量符号的由来再见谢谢大家的合作
不一定相同。所以 零向量只有一个,而单位向量可以有无数个:长度为 1 个单位长度的向量。三、几个特殊向量3.相等向量的定义:长度相等且方向相同的向量相反向量的定义:4.平行向量、共线向量的定义:基线平行或重合的向量叫做平行向量或共线向量。两向量的平行与平面几何里两线段的平行有什么区别?我们规定零向量与任一向量平行通过有向线段 的直线叫向量 的基线。即共线向量或平行向量的方向相同或相反。例1:已知O为正六边形ABCDEF的中心,
在图中所标出的向量中:解:分别以图中的格点为起点和终点作向量,练习一
1、单位向量是否一定相等?
2、单位向量的大小是否一定相等?BACK不一定一定练习二
1、平行向量是否一定方向相同?
2、不相等的向量一定不平行吗?BACK不一定不一定BACK练习三
1、与零向量相等的向量一定是什么向量?
2、与任意向量都平行的向量是什么向量?零向量零向量练习四
1、若两个向量在同一直线上,则这两个
向量是什么向量?
2、共线向量一定在一条直线上吗?共线向量 或者说平行向量不一定BACK练习五
在质量、重力、速度、身高、面积、体积这些量中,哪些是数量?哪些是向量?数量有:质量、身高、面积、体积向量有:重力、速度BACK在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终
点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等。正确的有:(4)练习六BACK练习七
1.设O为正△ABC的中心,则向量AO,BO,CO是 ( )
A.相等向量 B.模相等的向量
C.共线向量 D.共起点的向量
BABCOBACK练习八
命题:“│a│=│b│”成立,则“ a = b ”一定成
立×BACK练习九
1.已知a、b为不共线的非零向量,且
存在向量 c,使 c ∥ a, c ∥ b, 则
c =____BACK练习十
1.与非零向量 a 平行的向量中,
不相等的单位向量有_____个.2 BACK练习十一 如图,EF是△ABC的中位线,AD是BC 边上的中线,在以A、B、C、D、E、F为端点的有向线
段表示的向量中请分别写出
(1)与向量CD共线的向量有___个,
分别是______________________;
(2)与向量DF的模一定相等的向
量有__个,分别是_________________;
(3)与向量DE相等的向量有__个,
分别是___________。 ABCDEF752BACK如图,D、E、F分别是△ABC各边上的中点,四边形BCMF是平行四边形,请分别写出:
(1)与ED相等的向量;
(2)与ED共线的向量;
(3)与FE相等的向量;
(4)与FE共线的向量。ABCDFEM(1) 3个(2) 9个(3) 3个(4) 11个练习十二BACK课堂小结 向量最初被应用于物理学,被称为矢量.很多物理量,如力、速度、位移、电场强度、磁场强度等都是向量。
大约公元前350年,古希腊著名学者亚里士多德就知道了力可以表示为向量.向量一词来自力学、解析几何中的有向线段。
最先使用有向线段表示向量的是英国大科学家牛顿。课堂小结向量及向量符号的由来再见谢谢大家的合作
