2.2.1 平面向量基本定理 课件(20张PPT)
文档属性
| 名称 | 2.2.1 平面向量基本定理 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 223.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 09:20:56 | ||
图片预览





文档简介
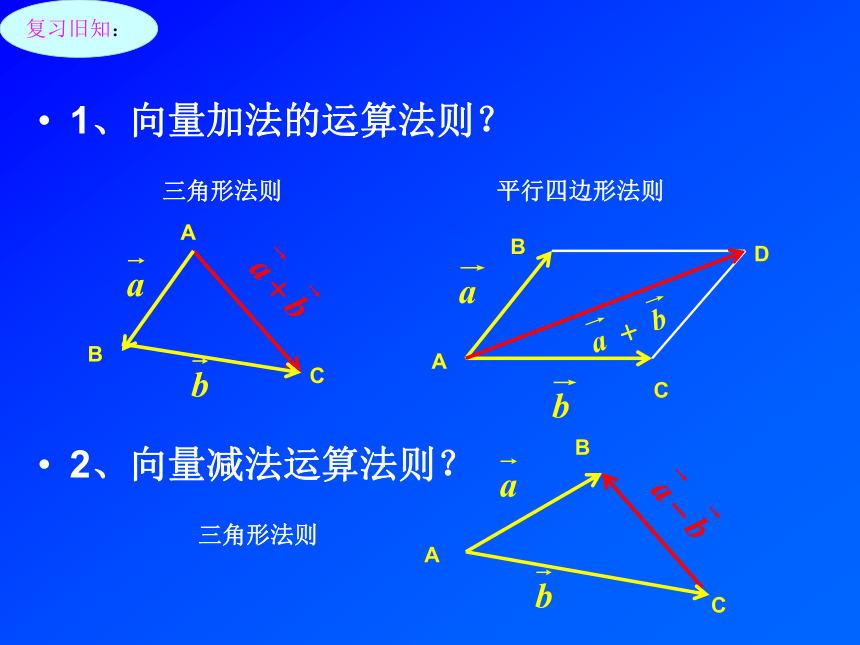
课件20张PPT。2.2.1 平面向量基本定理1、向量加法的运算法则?
2、向量减法运算法则?三角形法则平行四边形法则三角形法则复习旧知:3、平行向量基本定理的内容是什么?
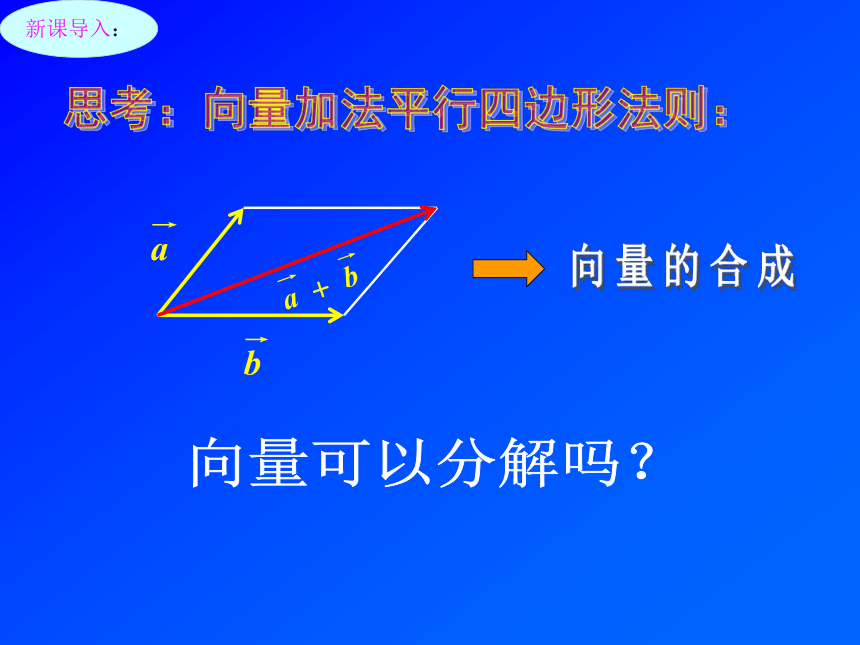
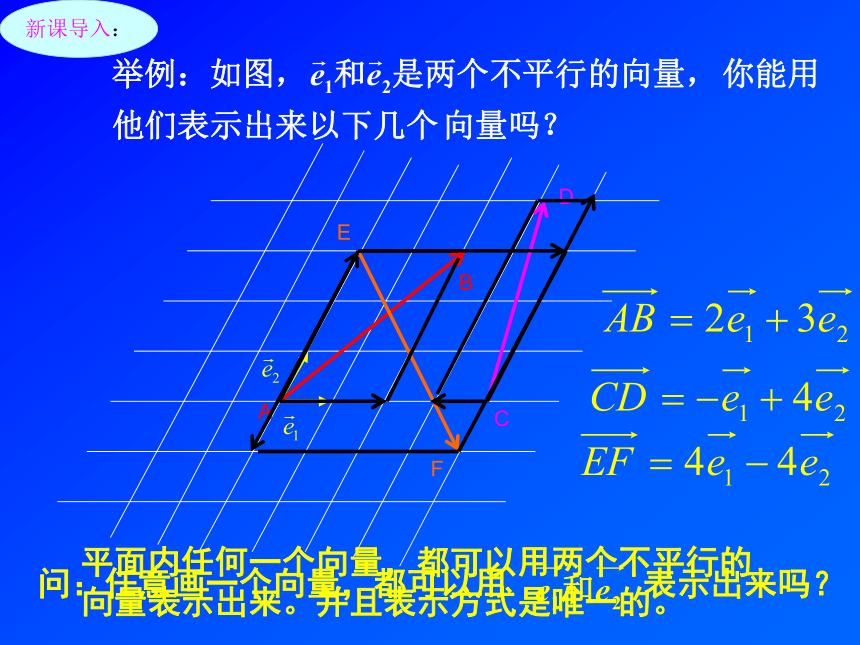
复习旧知:思考:向量加法平行四边形法则:向量可以分解吗?向量的合成新课导入:新课导入:问:任意画一个向量,都可以用 表示出来吗?平面内任何一个向量,都可以用两个不平行的向量表示出来。并且表示方式是唯一的。如果 和 是一平面内的两个不平行的向量,那
么该平面内的任一向量 ,存在唯一的一对实数
, ,使
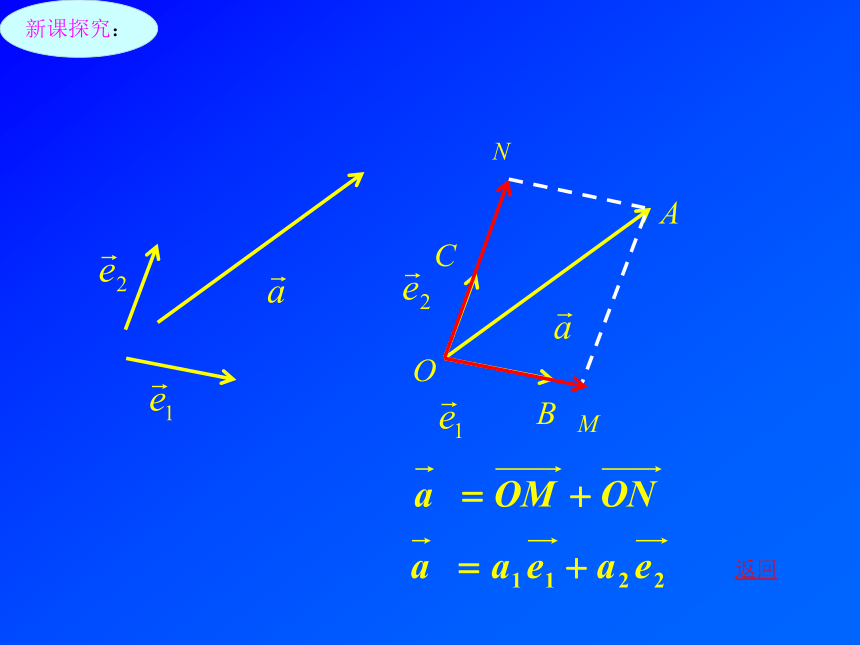
平面向量基本定理:新课探究:返回新课探究:假设不是唯一的,即存在另外一对实数x,y,
使新课探究: 分解式:如果 和 是一平面内的两个不平行的向量,那
么该平面内的任一向量 ,存在唯一的一对实数
, ,使
平面向量基本定理:基底:我们把不共线向量 , 叫做表示这一平面内所有向
量的一组基底,记为 。新课探究:新课探究:1、2、不可以不可以思考:3、4、平面内向量的基底是唯一的吗?
有多少对?无数对。任意不共线的两个向量都可以作为一组基底。新课探究:思考:例1、已知□ABCD的两条对角线相交于点 M,设 关键就是找出与基底的关系,通过向量的线性运算表示出来。课堂练习:例2、已知A、B是直线 上的任意两点,O是 外一点,求证:对直线 上的任意一点P,存在实数t,使 关于基底 的分解式为 并且,满足上式的点P一定在 上。 例2、已知A、B是直线 上的任意两点,O是 外一点,求证:对直线 上的任意一点P,存在实数t,使 关于基底 的分解式为 并且,满足上式的点P一定在 上。 1、在△OAP中,反之:设点P满足等式,也一定有
即点P在直线上。直线 的向量参数方程式,
实数t叫做参变数,
简称参数。
系数和为1课堂练习:AMNPBC课堂练习:本节课我们学习了:
一、平面向量基本定理的内容
1、基底不唯一,关键不共线
2、可表示平面内任一向量
3、选择基底后表示方法唯一。
二、平面向量基本定理的应用
1、直线的向量参数方程式
2、线段中点的向量表达式
课堂小结:作业: P98,3,4,5
预习下一节
布置作业:谢谢!再见!
2、向量减法运算法则?三角形法则平行四边形法则三角形法则复习旧知:3、平行向量基本定理的内容是什么?
复习旧知:思考:向量加法平行四边形法则:向量可以分解吗?向量的合成新课导入:新课导入:问:任意画一个向量,都可以用 表示出来吗?平面内任何一个向量,都可以用两个不平行的向量表示出来。并且表示方式是唯一的。如果 和 是一平面内的两个不平行的向量,那
么该平面内的任一向量 ,存在唯一的一对实数
, ,使
平面向量基本定理:新课探究:返回新课探究:假设不是唯一的,即存在另外一对实数x,y,
使新课探究: 分解式:如果 和 是一平面内的两个不平行的向量,那
么该平面内的任一向量 ,存在唯一的一对实数
, ,使
平面向量基本定理:基底:我们把不共线向量 , 叫做表示这一平面内所有向
量的一组基底,记为 。新课探究:新课探究:1、2、不可以不可以思考:3、4、平面内向量的基底是唯一的吗?
有多少对?无数对。任意不共线的两个向量都可以作为一组基底。新课探究:思考:例1、已知□ABCD的两条对角线相交于点 M,设 关键就是找出与基底的关系,通过向量的线性运算表示出来。课堂练习:例2、已知A、B是直线 上的任意两点,O是 外一点,求证:对直线 上的任意一点P,存在实数t,使 关于基底 的分解式为 并且,满足上式的点P一定在 上。 例2、已知A、B是直线 上的任意两点,O是 外一点,求证:对直线 上的任意一点P,存在实数t,使 关于基底 的分解式为 并且,满足上式的点P一定在 上。 1、在△OAP中,反之:设点P满足等式,也一定有
即点P在直线上。直线 的向量参数方程式,
实数t叫做参变数,
简称参数。
系数和为1课堂练习:AMNPBC课堂练习:本节课我们学习了:
一、平面向量基本定理的内容
1、基底不唯一,关键不共线
2、可表示平面内任一向量
3、选择基底后表示方法唯一。
二、平面向量基本定理的应用
1、直线的向量参数方程式
2、线段中点的向量表达式
课堂小结:作业: P98,3,4,5
预习下一节
布置作业:谢谢!再见!
