2.3.1 向量数量积的物理背景与定义 课件(19张PPT)
文档属性
| 名称 | 2.3.1 向量数量积的物理背景与定义 课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 09:36:04 | ||
图片预览



文档简介
课件19张PPT。向量数量积的物理背景与定义
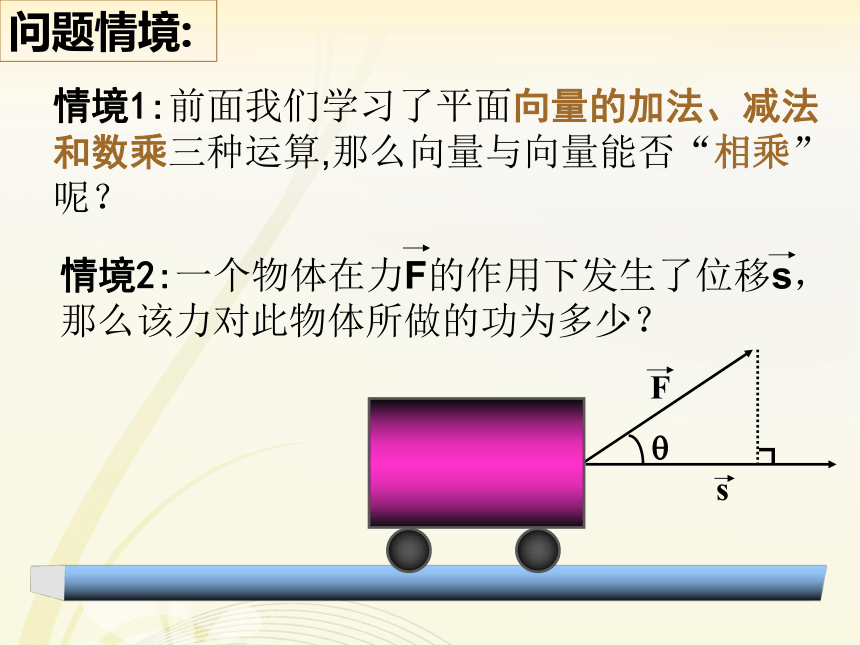
问题情境:情境1:前面我们学习了平面向量的加法、减法和数乘三种运算,那么向量与向量能否“相乘”呢? 一个物体在力 的作用下产生位移 ,
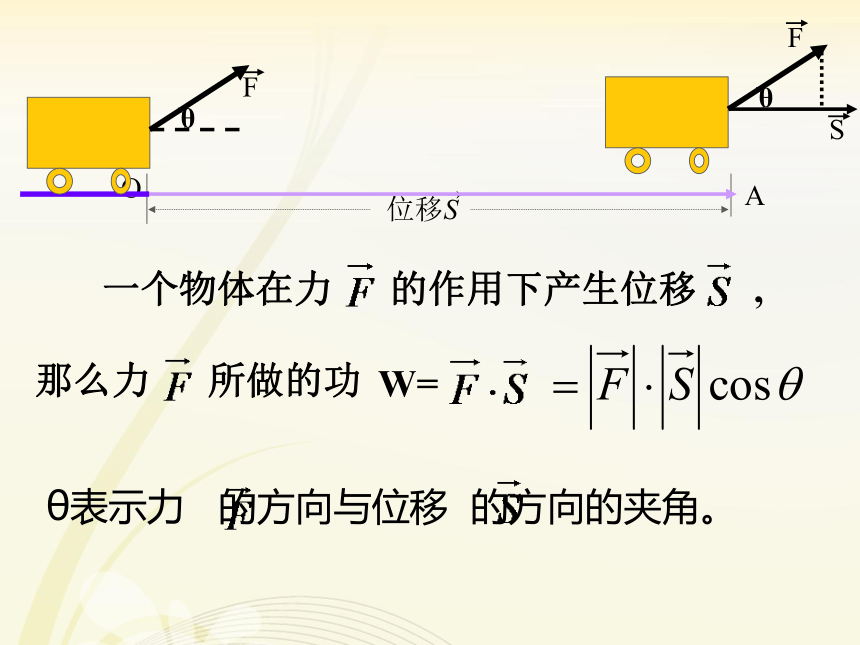
那么力 所做的功W=θ表示力 的方向与位移 的方向的夹角。一:向量的夹角已知两个非零向量a,b 如图
角θ称作向量a和向量b的夹角,
记作
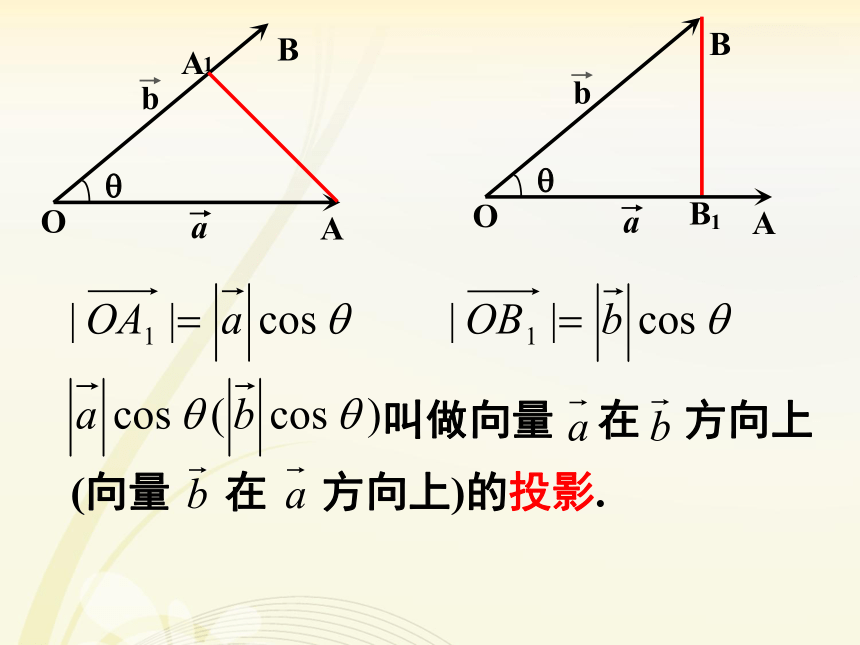
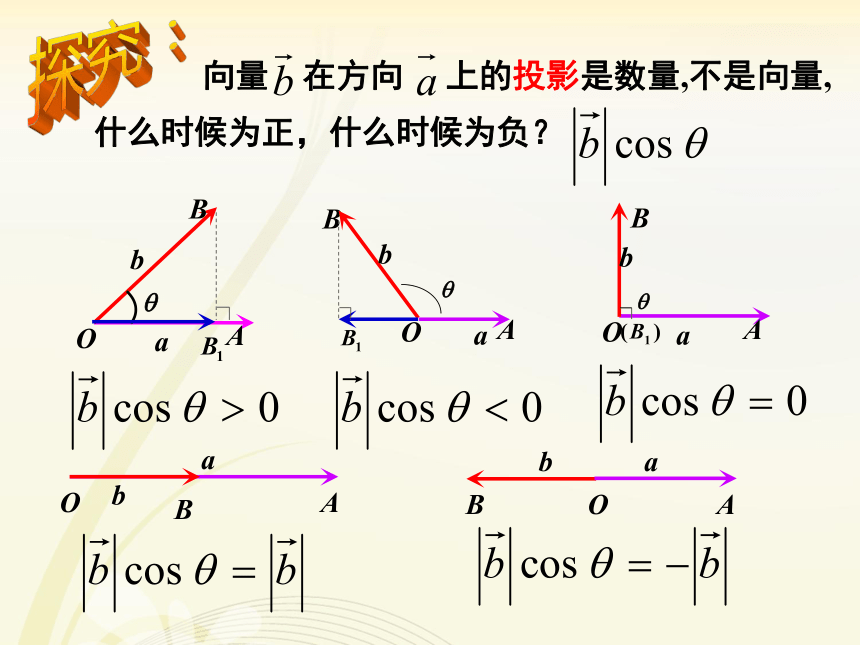
0≤≤π 向量 在方向 上的投影是数量,不是向量,什么时候为正,什么时候为负?探究: 我们将功的运算类比到两个向量的一种运算,得到向量“数量积”的概念。平面向量数量积的定义:规定:零向量与任意向量的数量积为0.注意: (1) 两个向量的数量积是一个实数,不是向量. (2)两个向量的数量积称为内积,写成 .性质注意: (3) 向量的数量积和实数与向量的积(数乘)不是一回事. 数量积 的结果是一个数量(实数);实数与向量的积(数乘)还是一个向量.练习:课本 109页 练习A 第一题向量数量积的性质当且仅当两向量共线时等号成立(B1)平面向量数量积几何意义│ │cosθ叫做向量 在向量 方向上的投影,
│ │cosθ叫做向量 在向量 方向上的投影.平面向量数量积的几何意义:1.向量a的模为10,它与x轴正方向的夹角为150°,则它在x轴上的投影为( )A【例3】 已知|a|=3,|b|=5,a·b=12,则向量a在向量b的方向上的投影为________.解析:(θ为a与b的夹角),1.下列命题中正确的是( )
A.|a·b|=|a|·|b| B.a·b≠b·a
C.(λa)·b≠a·(λb)
D.非零向量a与b的夹角余弦值为D3.在△ABC中,三个式子中可以成立的( )A.至少1个 B.至多1个
C.一个也没有 D.三式可以同时成立B作业:p109练习B1,2
问题情境:情境1:前面我们学习了平面向量的加法、减法和数乘三种运算,那么向量与向量能否“相乘”呢? 一个物体在力 的作用下产生位移 ,
那么力 所做的功W=θ表示力 的方向与位移 的方向的夹角。一:向量的夹角已知两个非零向量a,b 如图
角θ称作向量a和向量b的夹角,
记作
0≤
│ │cosθ叫做向量 在向量 方向上的投影.平面向量数量积的几何意义:1.向量a的模为10,它与x轴正方向的夹角为150°,则它在x轴上的投影为( )A【例3】 已知|a|=3,|b|=5,a·b=12,则向量a在向量b的方向上的投影为________.解析:(θ为a与b的夹角),1.下列命题中正确的是( )
A.|a·b|=|a|·|b| B.a·b≠b·a
C.(λa)·b≠a·(λb)
D.非零向量a与b的夹角余弦值为D3.在△ABC中,三个式子中可以成立的( )A.至少1个 B.至多1个
C.一个也没有 D.三式可以同时成立B作业:p109练习B1,2
