人教版数学必修5 1.2 应用举例(共25张ppt)
文档属性
| 名称 | 人教版数学必修5 1.2 应用举例(共25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 942.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 10:19:13 | ||
图片预览



文档简介
课件25张PPT。 解三角形的实际应用举例
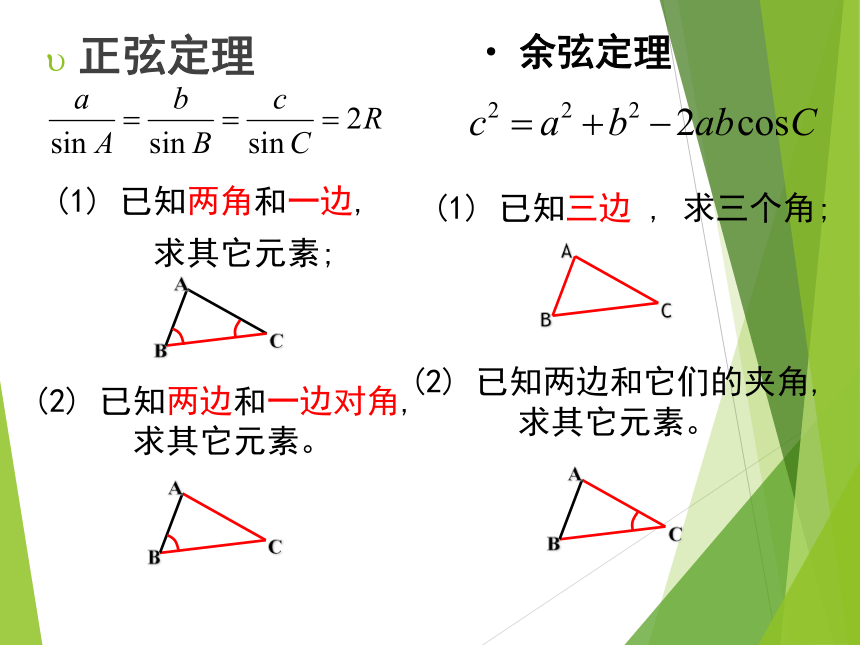
——高度、角度问题实际问题正弦定理余弦定理(1) 已知两角和一边,
求其它元素; 已知三边 , 求三个角;(2) 已知两边和一边对角,
求其它元素。(2) 已知两边和它们的夹角,
求其它元素。【知识提炼】
1.仰角和俯角
目标视线在水平线_____时叫仰角,目标视线在水平线_____
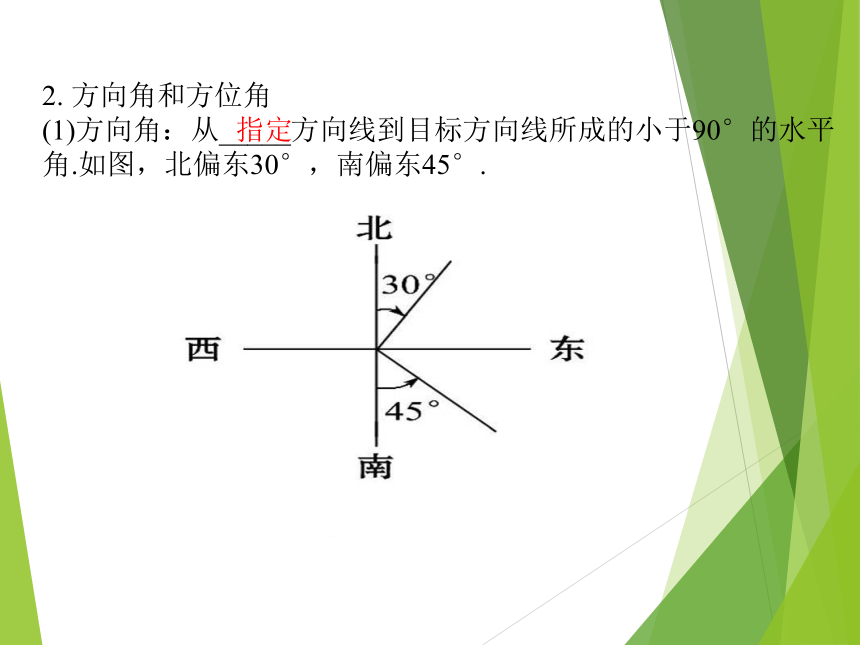
时叫俯角,如图所示.上方下方2. 方向角和方位角
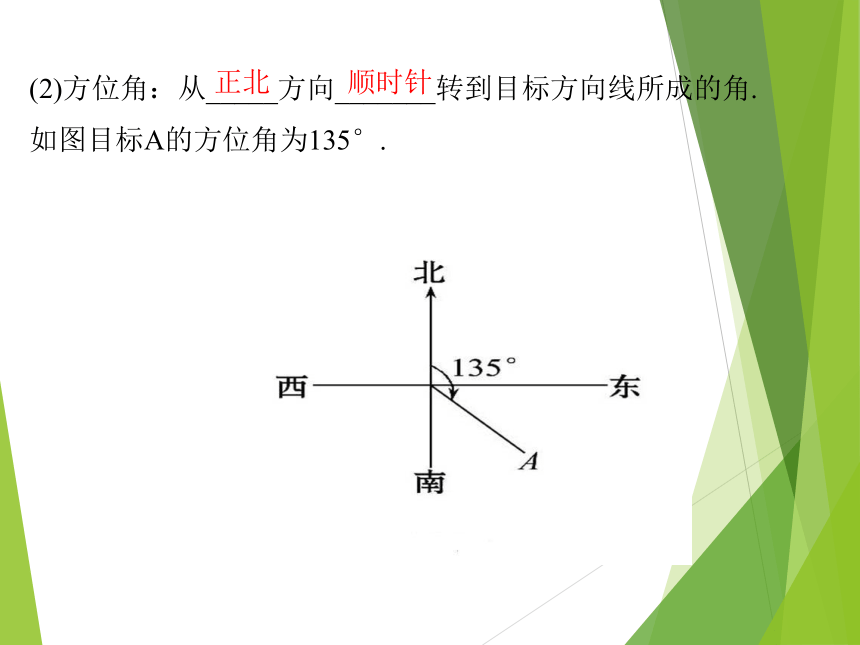
(1)方向角:从_____方向线到目标方向线所成的小于90°的水平角.如图,北偏东30°,南偏东45°.指定(2)方位角:从_____方向_______转到目标方向线所成的角.
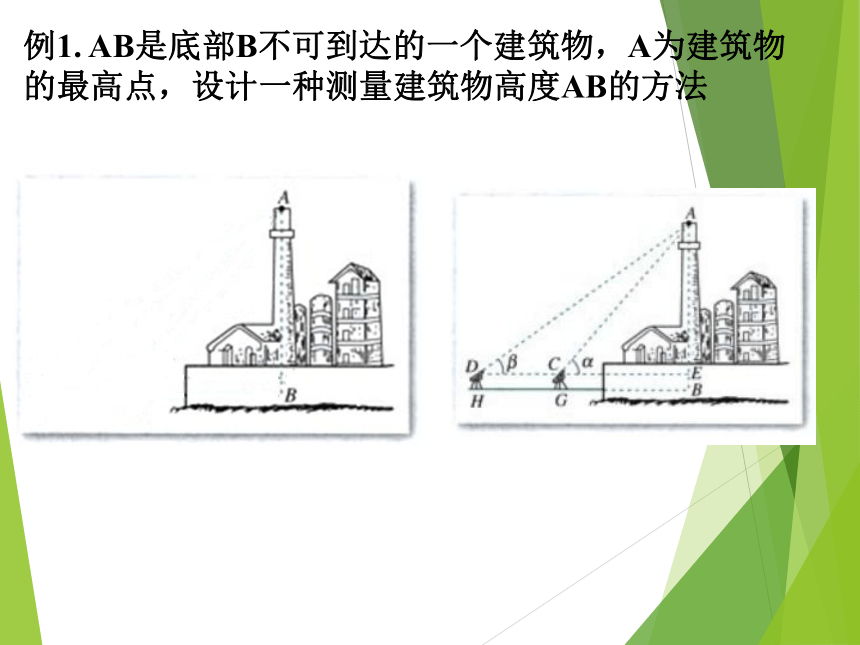
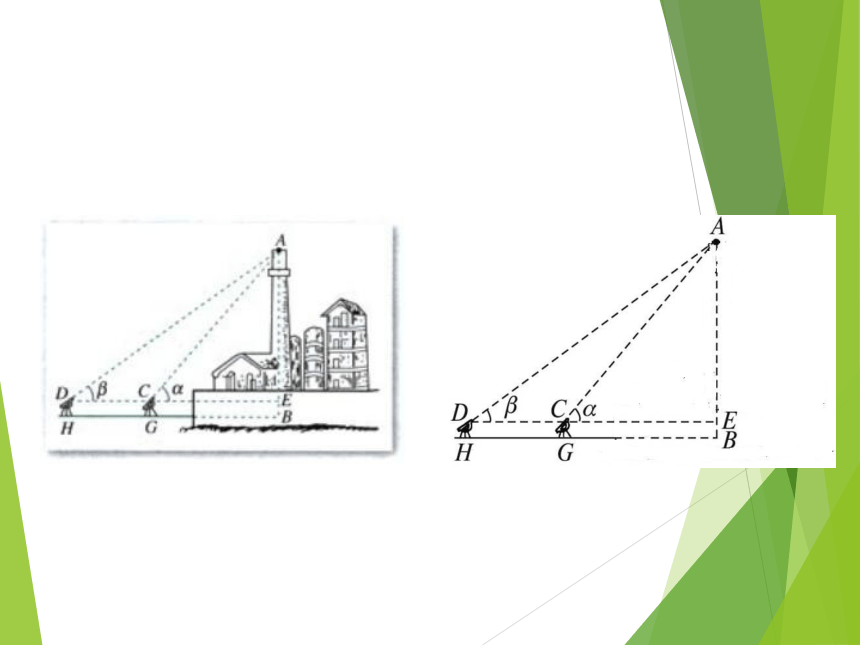
如图目标A的方位角为135°.正北顺时针例1. AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法 怎样测量一个底部不能到达的建筑物的高度?解:选择一条水平基线HG,使H,G,B三点在同一条直线上。由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.那么,在⊿ACD中,根据正弦定理可得 例2 如图,在山顶铁塔上B处测得地面上一点A的俯角 α=54°40′,在塔底C处测得A处的俯角β=50°1′ ,已知铁塔BC部分的高为27.3 m,求出山高CD(精确到1 m).【解析】在△ABC中,∠BCA=90°+β,∠ABC=90°-α,
∠BAC=α-β, ∠BAD=α.根据正弦定理,答:山的高度约为150米.把测量数据代入上式,得CD=BD-BC≈177.4-27.3≈150(m)..例3 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15°的方向上,行驶5 km后到达B处,测得此山顶在西偏北25°的方向上,仰角为8°,求此山的高CD(精确到1 m).例3. 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.解:在⊿ABC中,∠A=15°,
∠C=25°-15°=10°.
根据正弦定理,CD=BC×tan∠DBC≈BC×tan8°≈1047(m)答:山的高度约为1047米。【变式练习】【解析】在△ABC中,例4 如图,一艘海轮从A出发,沿北偏东75°的方向航行67.5 n mile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0 n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,
需要航行的距离是
多少?(角度精确到
0.1°,距离精确到
0.01 n mile)探究点2 测量角度问题【解析】在 △ABC中,∠ABC=180°-75°+32°=137°,根据余弦定理,根据正弦定理,【变式练习】如图,渔船甲位于岛屿A的南偏西60°方向的B处,
且与岛屿A相距12海里,渔船乙以10海里/小时的速
度从岛屿A出发沿正北方向航行,若渔船甲同时从B
处出发沿北偏东α的方向追赶渔船乙,刚好用2小时
追上.
(1)求渔船甲的速度;
(2)求sin α的值.
. 1.在200m的山顶上,测得山下一塔塔顶与塔底的
俯角分别为30°,60°,则塔高为_____随堂训练达标2.如图,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ
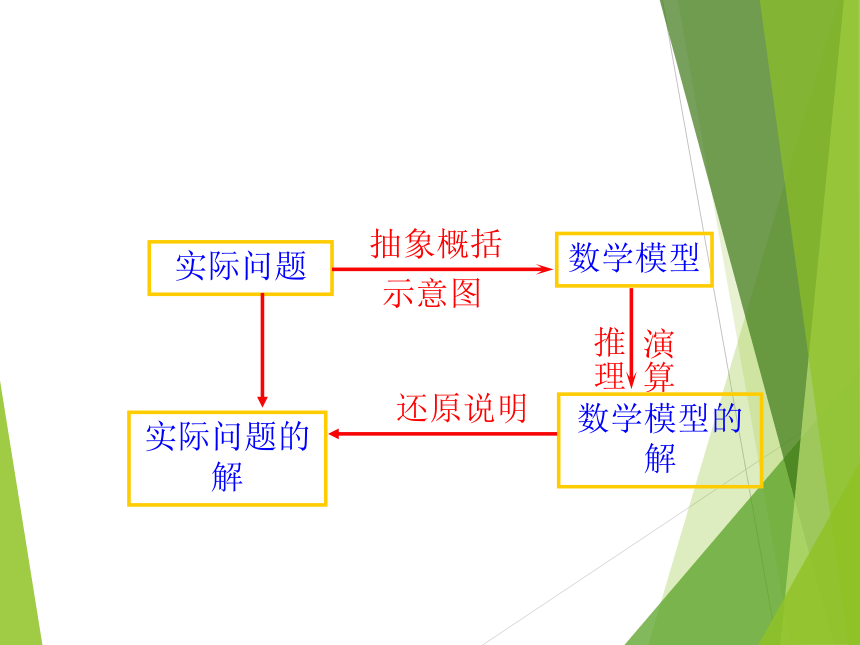
的方向沿直线CB前往B处救援,则cosθ= ?1.利用正弦定理和余弦定理解题时,要学会审题及根据题意画方位图,要懂得从所给的背景资料中加工、抽取主要因素,并进行适当简化.实际问题2.实际问题处理
——高度、角度问题实际问题正弦定理余弦定理(1) 已知两角和一边,
求其它元素; 已知三边 , 求三个角;(2) 已知两边和一边对角,
求其它元素。(2) 已知两边和它们的夹角,
求其它元素。【知识提炼】
1.仰角和俯角
目标视线在水平线_____时叫仰角,目标视线在水平线_____
时叫俯角,如图所示.上方下方2. 方向角和方位角
(1)方向角:从_____方向线到目标方向线所成的小于90°的水平角.如图,北偏东30°,南偏东45°.指定(2)方位角:从_____方向_______转到目标方向线所成的角.
如图目标A的方位角为135°.正北顺时针例1. AB是底部B不可到达的一个建筑物,A为建筑物的最高点,设计一种测量建筑物高度AB的方法 怎样测量一个底部不能到达的建筑物的高度?解:选择一条水平基线HG,使H,G,B三点在同一条直线上。由在H,G两点用测角仪器测得A的仰角分别是α,β,CD=a,测角仪器的高是h.那么,在⊿ACD中,根据正弦定理可得 例2 如图,在山顶铁塔上B处测得地面上一点A的俯角 α=54°40′,在塔底C处测得A处的俯角β=50°1′ ,已知铁塔BC部分的高为27.3 m,求出山高CD(精确到1 m).【解析】在△ABC中,∠BCA=90°+β,∠ABC=90°-α,
∠BAC=α-β, ∠BAD=α.根据正弦定理,答:山的高度约为150米.把测量数据代入上式,得CD=BD-BC≈177.4-27.3≈150(m)..例3 如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北15°的方向上,行驶5 km后到达B处,测得此山顶在西偏北25°的方向上,仰角为8°,求此山的高CD(精确到1 m).例3. 一辆汽车在一条水平的公路上向正东行驶,到A处时测得公路南侧远处一山顶D在东偏南15°的方向上,行驶5km后到达B处,测得此山顶在东偏南25°的方向上,仰角8°,求此山的高度CD.解:在⊿ABC中,∠A=15°,
∠C=25°-15°=10°.
根据正弦定理,CD=BC×tan∠DBC≈BC×tan8°≈1047(m)答:山的高度约为1047米。【变式练习】【解析】在△ABC中,例4 如图,一艘海轮从A出发,沿北偏东75°的方向航行67.5 n mile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0 n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,
需要航行的距离是
多少?(角度精确到
0.1°,距离精确到
0.01 n mile)探究点2 测量角度问题【解析】在 △ABC中,∠ABC=180°-75°+32°=137°,根据余弦定理,根据正弦定理,【变式练习】如图,渔船甲位于岛屿A的南偏西60°方向的B处,
且与岛屿A相距12海里,渔船乙以10海里/小时的速
度从岛屿A出发沿正北方向航行,若渔船甲同时从B
处出发沿北偏东α的方向追赶渔船乙,刚好用2小时
追上.
(1)求渔船甲的速度;
(2)求sin α的值.
. 1.在200m的山顶上,测得山下一塔塔顶与塔底的
俯角分别为30°,60°,则塔高为_____随堂训练达标2.如图,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ
的方向沿直线CB前往B处救援,则cosθ= ?1.利用正弦定理和余弦定理解题时,要学会审题及根据题意画方位图,要懂得从所给的背景资料中加工、抽取主要因素,并进行适当简化.实际问题2.实际问题处理
