人教A版数学必修4 1.2.1.任意角的三角函数(共15张ppt)
文档属性
| 名称 | 人教A版数学必修4 1.2.1.任意角的三角函数(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 00:00:00 | ||
图片预览


文档简介
课件15张PPT。欧拉(Euler Leonhard,
1707-1783) 三角函数在人类社会的各门科学技术中都有着非常广泛的应用,如:物理学中弹簧的简谐振动,潮汐,交通等。它充满了未知和神奇,使人们不断去探索研究应用它。三角函数的发展过程历经了 20个世纪。1748年瑞士著名的数学家和物理学家欧拉在《无穷小分析论》提出的三角函数定义,使三角学从原先静态研究三角形的解法中解脱出来,成为一门反映现实世界中某些运动和变化、具有现代数学特征的学科。欧拉不仅用直角坐标来定义三角函数,他还令圆的半径等于1,定义了单位圆,以相应线段与半径的比值定义三角函数,这样使得三角函数的定义更为简单。1.2.1
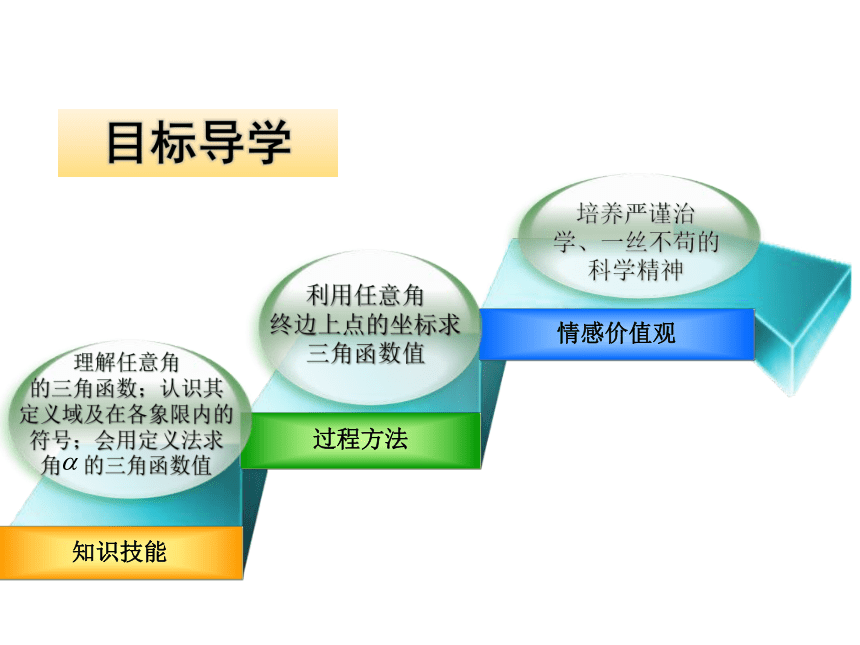
任意角的三角函数 知识技能过程方法情感价值观利用任意角
终边上点的坐标求
三角函数值培养严谨治
学、一丝不苟的
科学精神目标导学理解任意角
的三角函数;认识其
定义域及在各象限内的
符号;会用定义法求
角 的三角函数值
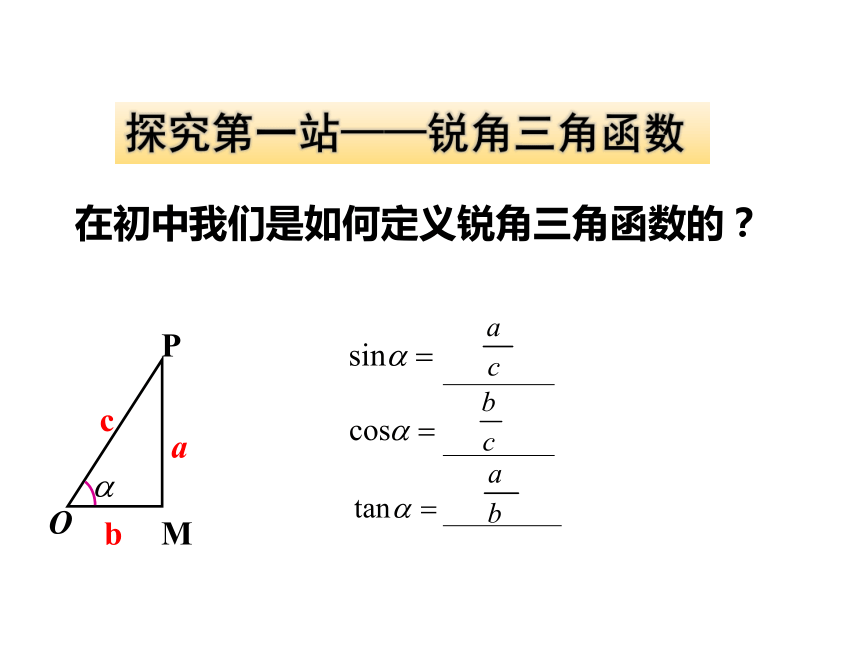
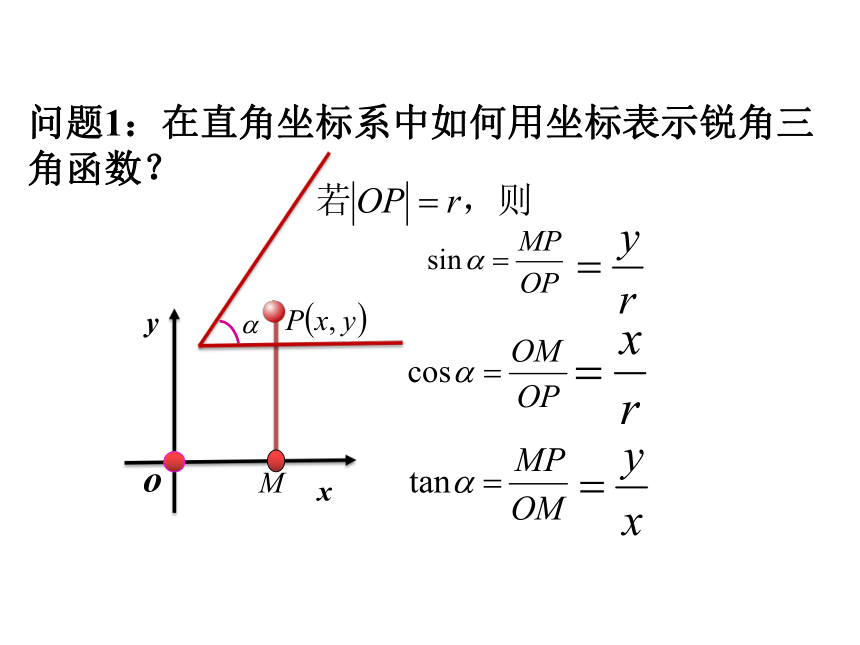
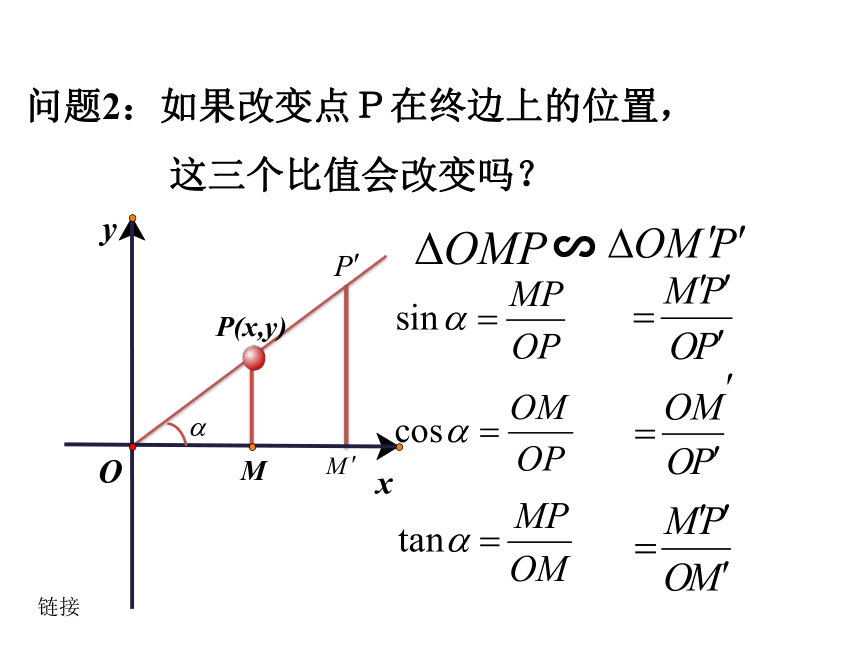
探究第一站——锐角三角函数在初中我们是如何定义锐角三角函数的?yx问题1:在直角坐标系中如何用坐标表示锐角三角函数?﹒o问题2:如果改变点P在终边上的位置,
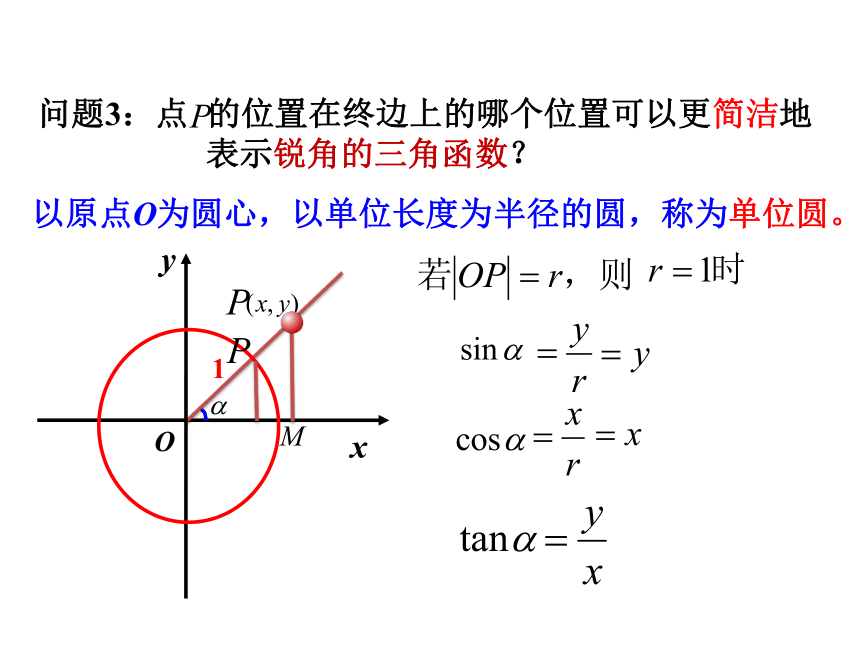
这三个比值会改变吗?∽MOyxP(x,y)链接yOx1M以原点O为圆心,以单位长度为半径的圆,称为单位圆。 问题3:点 的位置在终边上的哪个位置可以更简洁地表示锐角的三角函数?设 是一个任意角,它的终边与单位圆交于点 那么:(1) 叫做 的正弦,记作 ,即 ; (2) 叫做 的余弦,记作 ,即 ; (3) 叫做 的正切,记作 ,即 。 正弦,余弦,正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,它们统称为三角函数。﹒探究第二站—— 任意角的三角函数问题4:角有正角、负角和零角,在这样的环境下,你认为对于任意角 ,
如何来定义好呢?链接RR口诀“一全正, 二正弦,三正切,四余弦.”+--+--++-+-探究第三站例1.求 的正弦、余弦和正切值.的终边与单位圆的交点坐标为 所以 练习1:若把角 改为 呢? 于是, 例2.已知角 的终边经过点 ,求角
的正弦、余弦和正切值。解:由已知可得探究第四站—— 概念的推广链接那么① 叫做 的正弦,即 ② 叫做 的余弦,即③ 叫做 的正弦,即一般地,设角 是一个任意角, 是终边上的任意一点,
点 与原点的距离 .则角 的三角函数该如何定义?链接学完本节课,你有哪些收获、启示或感悟? 总结升华收获知识技能思想方法2.已知角 的终边过点 ,求 的三个三角函数值.学以致用
1707-1783) 三角函数在人类社会的各门科学技术中都有着非常广泛的应用,如:物理学中弹簧的简谐振动,潮汐,交通等。它充满了未知和神奇,使人们不断去探索研究应用它。三角函数的发展过程历经了 20个世纪。1748年瑞士著名的数学家和物理学家欧拉在《无穷小分析论》提出的三角函数定义,使三角学从原先静态研究三角形的解法中解脱出来,成为一门反映现实世界中某些运动和变化、具有现代数学特征的学科。欧拉不仅用直角坐标来定义三角函数,他还令圆的半径等于1,定义了单位圆,以相应线段与半径的比值定义三角函数,这样使得三角函数的定义更为简单。1.2.1
任意角的三角函数 知识技能过程方法情感价值观利用任意角
终边上点的坐标求
三角函数值培养严谨治
学、一丝不苟的
科学精神目标导学理解任意角
的三角函数;认识其
定义域及在各象限内的
符号;会用定义法求
角 的三角函数值
探究第一站——锐角三角函数在初中我们是如何定义锐角三角函数的?yx问题1:在直角坐标系中如何用坐标表示锐角三角函数?﹒o问题2:如果改变点P在终边上的位置,
这三个比值会改变吗?∽MOyxP(x,y)链接yOx1M以原点O为圆心,以单位长度为半径的圆,称为单位圆。 问题3:点 的位置在终边上的哪个位置可以更简洁地表示锐角的三角函数?设 是一个任意角,它的终边与单位圆交于点 那么:(1) 叫做 的正弦,记作 ,即 ; (2) 叫做 的余弦,记作 ,即 ; (3) 叫做 的正切,记作 ,即 。 正弦,余弦,正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,它们统称为三角函数。﹒探究第二站—— 任意角的三角函数问题4:角有正角、负角和零角,在这样的环境下,你认为对于任意角 ,
如何来定义好呢?链接RR口诀“一全正, 二正弦,三正切,四余弦.”+--+--++-+-探究第三站例1.求 的正弦、余弦和正切值.的终边与单位圆的交点坐标为 所以 练习1:若把角 改为 呢? 于是, 例2.已知角 的终边经过点 ,求角
的正弦、余弦和正切值。解:由已知可得探究第四站—— 概念的推广链接那么① 叫做 的正弦,即 ② 叫做 的余弦,即③ 叫做 的正弦,即一般地,设角 是一个任意角, 是终边上的任意一点,
点 与原点的距离 .则角 的三角函数该如何定义?链接学完本节课,你有哪些收获、启示或感悟? 总结升华收获知识技能思想方法2.已知角 的终边过点 ,求 的三个三角函数值.学以致用
