2019-2020学年高中数学新人教A版必修1课件:第三章函数的应用3.2.1几类不同增长的函数模型课件 20张
文档属性
| 名称 | 2019-2020学年高中数学新人教A版必修1课件:第三章函数的应用3.2.1几类不同增长的函数模型课件 20张 |

|
|
| 格式 | zip | ||
| 文件大小 | 360.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 10:43:42 | ||
图片预览







文档简介
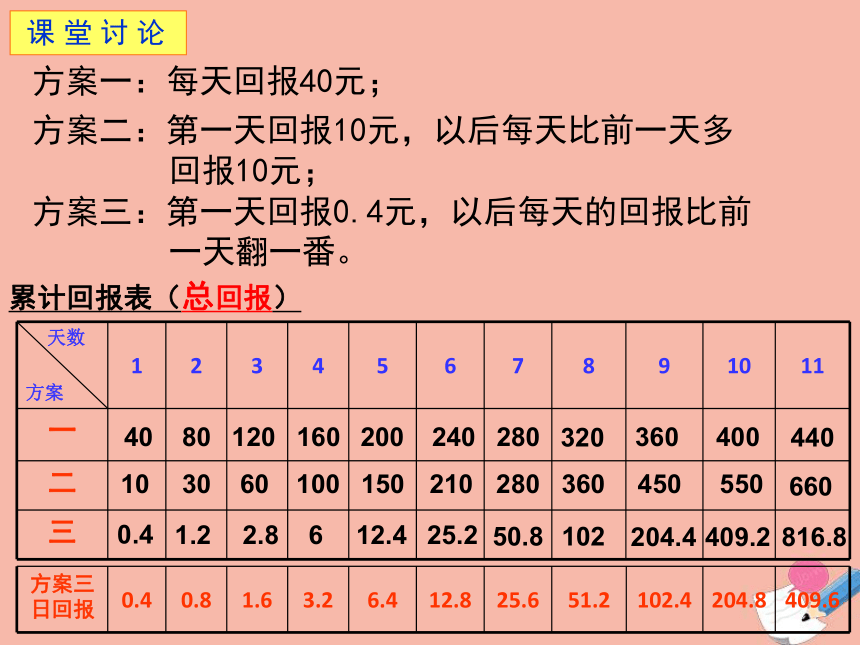
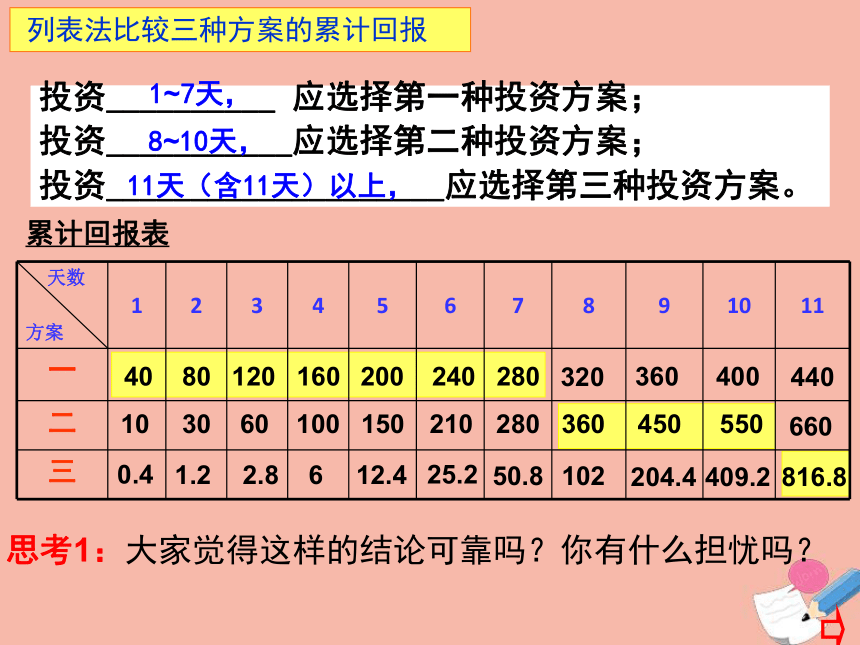
课件20张PPT。 3.2.1几类不同增长函数模型招 聘 启 事 猪氏集团因业务发展需要,即可录用,待遇丰厚.特招聘旗下餐饮公司经理一名.要求30周岁以下,经面试合格,联 系 人 :猪 悟能联系电话:86868866 “天棚大酒店”自2013年1月1号营业以来,生意蒸蒸日上.第一个月的营业额就达到了100万元,第二个月达到了150万元.第三个月的营业额为200万元,照此增长,第四个月的营业额为多少?又已知面试题目业额没超过500万,且在13年内,一月份到其他任何一个月份的营业额的月平均增长量不超过50万.第10个月的营问题2:进入高中以来,我们所学的函数中,哪些是符合在 上单调递增? 问题:上述猪八戒的营业额函数模型是否满足过点(1.1)(1,1.5)?例1.假如你有一笔资金用于投资,现有三种方案供你选择,这三种方案的回报如下:方案一:每天回报40元;方案二:第一天回报10元,以后每天比前一天多 回报10元;方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。请问,你会选择哪种投资方案? 提 出 问 题方案一:每天回报40元;方案二:第一天回报10元,以后每天比前一天多 回报10元;方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。 课 堂 讨 论累计回报表(总回报)40801201602002402803203604004401030601001502102803604505506600.41.22.8612.425.250.8102204.4409.2816.8累计回报表40801201602002402803203604004401030601001502102803604505506600.41.22.8612.425.250.8102204.4409.2816.8投资__________ 应选择第一种投资方案;
投资___________应选择第二种投资方案;
投资____________________应选择第三种投资方案。11天(含11天)以上,8~10天, 1~7天, 列表法比较三种方案的累计回报思考1:大家觉得这样的结论可靠吗?你有什么担忧吗?方案一:每天回报40元; 方案二:第一天回报10元,以后每天比前一天多 回报10元;方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。 课 堂 讨 论思考2:各方案每天回报的变化情况可用什么函数模型去刻画?12346578910200406080100120140y1020300.40.81.63.26.412.825.651.2102.4204.8图象法比较三种方案日回报量y=40y=10xy=0.4×2x-1x… 列表法比较三种方案的日回报量0.40.8运用规律, 解决问题例2、某公司2013年为了实现1000万元总利润的目标,他准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合公司的要求呢?思考4:本题中符合公司要求的
模型有什么条件?销售利润X的取值范围:奖金y满足的条件:三种奖金模型的函数模型增量△y增量△y增量△y2550751004.374.444.54.550.350.210.150.113.373.723.934.081.221.491.822.22反思① 此例涉及了哪几类函数模型?本例实质如何?
② 根据问题中的数据,如何判定所给的奖励模型是否符合公司要求? 练习1. 如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(月)的近似函数关系:(t≥0,a>0且a≠1).有以下叙述
第4个月时,剩留量就会低于1/5;
每月减少的有害物质量都相等;
若剩留量 为所经过的时间分别是 ,则 .
其中所有正确的叙述是 .2.经市场调查分析知,某地明年从年初开始的前n个月,对某种商品需求总量 f(n)(万件)近似地满足关系
(1)
写出明年第n个月这种商品需求量 g(n)(万件)与月份的函数关系式.指数爆炸 数学实验把厚度一样的纸一张一张叠上去…… 把一张纸不断地对折下去…… 现有一些厚度为0.1mm的纸实验1:叠实验2:折 实际问题万万千,增长模型千千万,数据图形细细看,感 悟人生高峰节节攀,选择爆炸直观拼搏数学模型来刻画.唯有指数最震撼.数形结合是思想.无限风光展未来.1.请同学谈谈你对几类不同增长的函数模型(一次函数、指数函数、对数函数)差异的认识。2. 几类增长函数建模的步骤列解析式具体问题画出图像(形)列出表格(数)不同增长确定模型预报和决策控制和优化3. 你还有其他感悟吗? 随 堂 小结没有增长直线增长指数爆炸对数增长
投资___________应选择第二种投资方案;
投资____________________应选择第三种投资方案。11天(含11天)以上,8~10天, 1~7天, 列表法比较三种方案的累计回报思考1:大家觉得这样的结论可靠吗?你有什么担忧吗?方案一:每天回报40元; 方案二:第一天回报10元,以后每天比前一天多 回报10元;方案三:第一天回报0.4元,以后每天的回报比前 一天翻一番。 课 堂 讨 论思考2:各方案每天回报的变化情况可用什么函数模型去刻画?12346578910200406080100120140y1020300.40.81.63.26.412.825.651.2102.4204.8图象法比较三种方案日回报量y=40y=10xy=0.4×2x-1x… 列表法比较三种方案的日回报量0.40.8运用规律, 解决问题例2、某公司2013年为了实现1000万元总利润的目标,他准备制定一个激励销售部门的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随着销售利润x (单位:万元)的增加而增加,但奖金数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:y=0.25x,y=log7x+1,y=1.002x,其中哪个模型能符合公司的要求呢?思考4:本题中符合公司要求的
模型有什么条件?销售利润X的取值范围:奖金y满足的条件:三种奖金模型的函数模型增量△y增量△y增量△y2550751004.374.444.54.550.350.210.150.113.373.723.934.081.221.491.822.22反思① 此例涉及了哪几类函数模型?本例实质如何?
② 根据问题中的数据,如何判定所给的奖励模型是否符合公司要求? 练习1. 如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(月)的近似函数关系:(t≥0,a>0且a≠1).有以下叙述
第4个月时,剩留量就会低于1/5;
每月减少的有害物质量都相等;
若剩留量 为所经过的时间分别是 ,则 .
其中所有正确的叙述是 .2.经市场调查分析知,某地明年从年初开始的前n个月,对某种商品需求总量 f(n)(万件)近似地满足关系
(1)
写出明年第n个月这种商品需求量 g(n)(万件)与月份的函数关系式.指数爆炸 数学实验把厚度一样的纸一张一张叠上去…… 把一张纸不断地对折下去…… 现有一些厚度为0.1mm的纸实验1:叠实验2:折 实际问题万万千,增长模型千千万,数据图形细细看,感 悟人生高峰节节攀,选择爆炸直观拼搏数学模型来刻画.唯有指数最震撼.数形结合是思想.无限风光展未来.1.请同学谈谈你对几类不同增长的函数模型(一次函数、指数函数、对数函数)差异的认识。2. 几类增长函数建模的步骤列解析式具体问题画出图像(形)列出表格(数)不同增长确定模型预报和决策控制和优化3. 你还有其他感悟吗? 随 堂 小结没有增长直线增长指数爆炸对数增长
