2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念1.2函数的概念课件 62张PPT
文档属性
| 名称 | 2019-2020学年高中数学新人教A版必修1课件:第一章集合与函数概念1.2函数的概念课件 62张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 10:51:39 | ||
图片预览





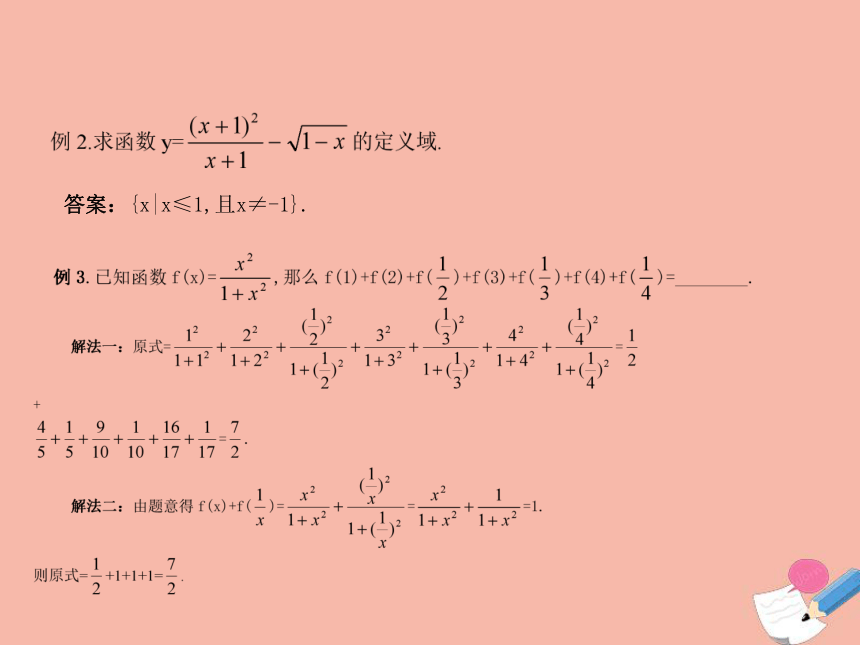



文档简介
课件62张PPT。 1.2.1函数的概念(第一课时)问题1:给出下列三种对应:
①一枚炮弹发射后,经过26 s落到地面击中目标.炮弹的射高为845 m,
且炮弹距地面的高度为h(单位:m)随时间t(单位:s)变化的规律是h=130t-5t2.
时间t的变化范围是数集A={t|0≤t≤26},h的变化范围是数集B={h|0≤h≤845}.
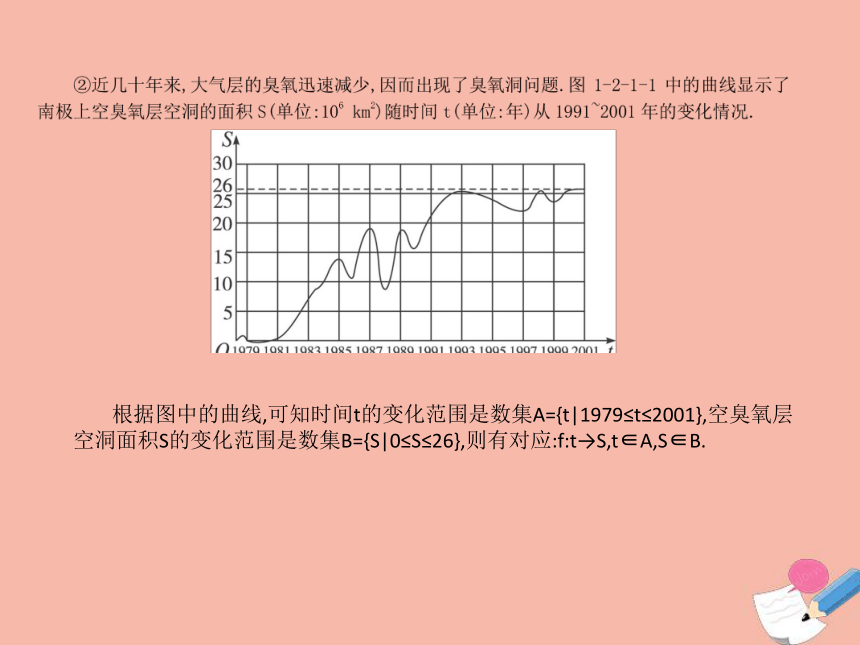
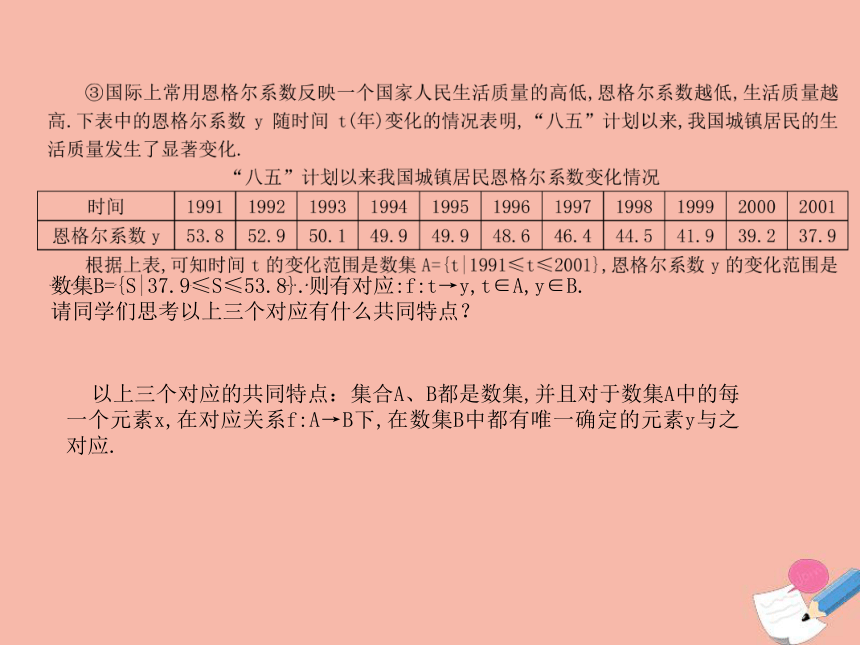
则有对应f:t→h=130t-5t2,t∈A,h∈B. 根据图中的曲线,可知时间t的变化范围是数集A={t|1979≤t≤2001},空臭氧层空洞面积S的变化范围是数集B={S|0≤S≤26},则有对应:f:t→S,t∈A,S∈B.数集B={S|37.9≤S≤53.8}.则有对应:f:t→y,t∈A,y∈B.
请同学们思考以上三个对应有什么共同特点?以上三个对应的共同特点:集合A、B都是数集,并且对于数集A中的每一个元素x,在对应关系f:A→B下,在数集B中都有唯一确定的元素y与之对应.1、函数的定义:
一般地,设A、B都是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A,其中x叫自变量。x的取值范围A叫做函数的定义域,函数值的集合{f(x)|x∈A}叫做函数的值域.
问题2:函数的定义域是自变量的取值范围,那么如何理解这个“取值范围”的?
? 自变量的取值范围就是使函数有意义的自变量的取值范围.
问题3:函数有意义又指什么?
函数有意义是指:自变量的取值使分母不为0;被开方数为非负数;如果函数有实际意义时,那么还要满足实际取值等.
?问题4:函数f:A→B的值域为C,那么集合B=C吗?答案:{x|x≤1,且x≠-1}.变式小结
请同学们回想一下,这节课我们学了哪些内容?作业 1.2.1函数的概念(第二课时)两个函数不相等,主要是定义域不同问题2:指出函数y=x+1的构成要素有几部分?并思考一个函数的构成要素有几部分?①函数y=x+1的构成要素为:定义域R,对应关系x→x+1,值域是R.
②一个函数的构成要素为:定义域、对应关系和值域,简称为函数的三要素.其中定义域是函数的灵魂,对应关系是函数的核心.当且仅当两个函数的三要素都相同时,这两个函数才相同.定义域和对应关系分别相同.问题4:函数y=x+1和函数y=t+1的值域相同吗?两个函数的值域相同,都是R.问题5:根据问题3和问题4的研究,分析两个函数的定义域和对应关系分别相同,值域一定相同吗?由此你对函数的三要素有什么新的认识?函数相等的条件:
如果两个函数的定义域和对应关系分别相同,那么它们的值 域一定相等.因此只要两个函数的定义域和对应关系分别相同,那 么这两个函数就相等.变式答案:-1小结:本节学了哪些内容?
(1)复习了函数的概念,总结了函数的三要素;
(2)学习了复合函数的概念;
(3)判断两个函数是否是同一个函数. 1.2.2函数的表示法(第一课时) 语言是沟通人与人之间的联系的,同样的祝福又有着不同的表示方法.例如,简体中文中的“生日快乐!”用繁体中文为:生日快樂!英文为:Happy Birthday!法文是Bon Anniversaire!德文是Alles Gute Zum Geburtstag!西班牙中称iFeliz CumpleaRos!印度尼西亚文是Selamat Ulang Tahun!荷兰文的生日快乐为Van Harte Gefeliciteerd met jeverj aardag!在俄语中则是С днем рождения!……
问题1:对于函数,又有什么不同的表示方法呢?引出课题——函数的表示法问题2:分析对比三种不同表示方法的优缺点?函数的三种表示方法:
解析法:用数学表达式表示两个变量之间的函数关系,这种表示方法叫做解析法,这个数学表达式叫做函数的解析式.
图象法:以自变量x的取值为横坐标,对应的函数值y为纵坐标,在平面直角坐标系中描出各个点,这些点构成了函数的图象,这种用图象表示两个变量之间函数关系的方法叫做图象法.
列表法:列一个两行多列的表格,第一行是自变量的取值,第二行是对应的函数值,这种用表格来表示两个变量之间的函数关系的方法叫做列表法.解析法能够准确表达出两个变量之间的关系,不足之处,比较抽象;图像形象直观表示两个变量之间的关系,不足之处,变量关系不够精确;列表法通过列表直观的得出两个变量的关系,不足之处,不能列出定义域为区间范围的函数,列表表示函数仅能表示有限个。例1.某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元,试用三种表示法表示函数y=f(x).4.车管站在某个星期日保管的自行车和电动车共有3 500辆次,其中电动车保管费是每辆一次0.5元,自行车保管费是每次一辆0.3元.
(1)若设自行车停放的辆次数为x,总的保管费收入为y元,试写出y关于x的函数关系式;
(2)若估计前来停放的3 500辆次自行车中,电动车的辆次不小于25%,但不大于40%,试求该保管站这个星期日收入保管费总数的范围.解:(1)由题意得
y=0.3x+0.5(3500-x)=-0.2x+1750,x∈N*且0≤x≤3500.
(2)若电动车的辆次不小于25%,但不大于40%,
则3500×(1-40%)≤x≤3 500×(1-25%),
即2100≤x≤2 625,
画出函数y=-0.2x+1750(2 100≤x≤2 625)的图象,可得
函数y=-0.2x+1750(2100≤x≤2625)的值域是[1225,1330],
即收入在1225元至1330元之间.小结
请同学们回想一下,这节课我们学了哪些函数的表示方法?在具体的实际问题中如何恰当地选择?
?作业
课本习题1.2A组7、8、9. 1.2.2函数的表示法(第二课时)问题1:当x>1时,f(x)=x+1;当x≤1时,f(x)=-x,请写出函数f(x)的解析式. 问题2:这个函数的解析式有什么特点?函数h(x)是分段函数,在定义域的不同部分,其解析式不同.2、分段函数是一个函数,不要把它误认为是几个函数问题4:分段函数是一个函数,那它的定义域和值域是什么?3、分段函数的定义域是各段定义域的并集,值域是各段值域的并集问题5:同学们能否举出生活中用分段函数描述的实际问题?如出租车的计费、个人所得税纳税额等。1、分段函数的定义:指在定义域的不同部分,有不同对应法则的函数.例1.画出函数y=|x|的图象.小结:本节课我们学了哪些内容,请同学们进行回顾和总结.作业课本P25习题1.2 B组 3、4. 1.2.2函数的表示法(第三课时) 前面学习了函数的概念是:一般地,设A,B是两个非空数集,如果按照某种对应法则f,对于集合A中的每个元素x,在集合B中都有唯一的元素y和它对应.
(1)对于任意一个实数,在数轴上都有唯一的点与之对应.
(2)班级里的一位同学在教室都有唯一的坐位与之对应.
(3)对于任意的三角形,都有唯一确定的面积与之对应.
那么这些对应又有什么特点呢?
?这种对应称为映射.结论:
①集合A、B均为非空集合,并且集合A中的元素在集合B中都有唯一的元素与之对应.
②一般地,设A、B是两个非空的集合,如果按某一个确定的对应法则f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射.记作“f:A→B”.
如果集合A中的元素x对应集合B中元素y,那么集合A中的元素x叫集合B中元素y的原象,集合B中元素y叫集合A中的元素x的象.
③包含两层意思:一是必有一个;二是只有一个,也就是说有且只有一个的意思,即是一对一或多对一.
④函数是特殊的映射,映射是函数的推广.例1.下列哪些对应是从集合A到集合B的映射?
(1)A={P|P是数轴上的点},B=R,对应关系f:数轴上的点与它所代表的实数对应;
(2)A={P|P是平面直角坐标系中的点},B={(x,y)|x∈R,y∈R},对应关系f:平面直角坐标系中的点与它的坐标对应;
(3)A={三角形},B={x|x是圆},对应关系f:每一个三角形都对应它的内切圆;
(4)A={x|x是新华中学的班级},B={x|x是新华中学的学生},对应关系f:每一个班级都对应班里的学生.解:(1)是映射;(2)是映射;(3)是映射;
(4)不是映射.新华中学的每个班级对应其班内的多个学生,是一对多,不符合映射的定义.例2.下列对应是不是从集合A到集合B的映射,为什么?
(1)A=R,B={x∈R|x≥0},对应法则是“求平方”;
(2)A=R,B={x∈R|x>0},对应法则是“求平方”;
(3)A={x∈R|x>0},B=R,对应法则是“求平方根”;
(4)A={平面内的圆},B={平面内的矩形},对应法则是“作圆的内接矩形”.解:(1)是映射,因为A中的任何一个元素,在B中都能找到唯一的元素与之对应.
(2)不是从集合A到集合B的映射,因为A中的元素0,在集合B中没有对应的元素.
(3)不是从集合A到集合B的映射,因为任何正数的平方根都有两个值,即集合A中的任何元素,在集合B中都有两个元素与之对应.
(4)不是从集合A到集合B的映射.因为一个圆有无穷多个内接矩形,即集合A中任何一个元素在集合B中有无穷多个元素与之对应.例3.设f:A→B是A到B的一个映射,其中A=B={(x,y)|x,y∈R},f:(x,y)→(x-y,x+y),求:
(1)A中元素(-1,2)在B中对应的元素;
(2)在A中什么元素与B中元素(-1,2)对应?1.设映射f:x→-x2+2x是实数集R=M到实数集R=N的映射,若对于实数p∈N,在M中不存在原象,则实数p的取值范围是( )
A.(1,+∞) B.[1,+∞) C.(-∞,1) D.(-∞,1]分析:f(a)表示在对应法则f下a对应的象,g(a)表示在对应法则g下a对应的象.
由表1和表2,得f[g(1)]=f(4)=1,g[f(1)]=g(3)=1,g[f(2)]=g(4)=2,g[f(3)]=g(2)=3,g[f(4)]=g(1)=4,
则有f[g(1)]=g[f(1)]=1,
故选A.
答案:A3.设集合A={a,b,c},集合B=R,以下对应关系中,一定能建立集合A到集合B的映射的是( )
A.对集合A中的数开平方
B.对集合A中的数取倒数
C.对集合A中的数取算术平方根
D.对集合A中的数立方分析:当a<0时,对a开平方或取算术平方根均无意义,则A、C错;当a=0时,对a取倒数无意义,则B错;由于对任何实数都能立方,并且其立方仅有一个,所以对集合A中的数立方能建立映射,故选D.
答案:D小结
请同学们回想一下,这节课我们学了哪些内容?
①一枚炮弹发射后,经过26 s落到地面击中目标.炮弹的射高为845 m,
且炮弹距地面的高度为h(单位:m)随时间t(单位:s)变化的规律是h=130t-5t2.
时间t的变化范围是数集A={t|0≤t≤26},h的变化范围是数集B={h|0≤h≤845}.
则有对应f:t→h=130t-5t2,t∈A,h∈B. 根据图中的曲线,可知时间t的变化范围是数集A={t|1979≤t≤2001},空臭氧层空洞面积S的变化范围是数集B={S|0≤S≤26},则有对应:f:t→S,t∈A,S∈B.数集B={S|37.9≤S≤53.8}.则有对应:f:t→y,t∈A,y∈B.
请同学们思考以上三个对应有什么共同特点?以上三个对应的共同特点:集合A、B都是数集,并且对于数集A中的每一个元素x,在对应关系f:A→B下,在数集B中都有唯一确定的元素y与之对应.1、函数的定义:
一般地,设A、B都是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A,其中x叫自变量。x的取值范围A叫做函数的定义域,函数值的集合{f(x)|x∈A}叫做函数的值域.
问题2:函数的定义域是自变量的取值范围,那么如何理解这个“取值范围”的?
? 自变量的取值范围就是使函数有意义的自变量的取值范围.
问题3:函数有意义又指什么?
函数有意义是指:自变量的取值使分母不为0;被开方数为非负数;如果函数有实际意义时,那么还要满足实际取值等.
?问题4:函数f:A→B的值域为C,那么集合B=C吗?答案:{x|x≤1,且x≠-1}.变式小结
请同学们回想一下,这节课我们学了哪些内容?作业 1.2.1函数的概念(第二课时)两个函数不相等,主要是定义域不同问题2:指出函数y=x+1的构成要素有几部分?并思考一个函数的构成要素有几部分?①函数y=x+1的构成要素为:定义域R,对应关系x→x+1,值域是R.
②一个函数的构成要素为:定义域、对应关系和值域,简称为函数的三要素.其中定义域是函数的灵魂,对应关系是函数的核心.当且仅当两个函数的三要素都相同时,这两个函数才相同.定义域和对应关系分别相同.问题4:函数y=x+1和函数y=t+1的值域相同吗?两个函数的值域相同,都是R.问题5:根据问题3和问题4的研究,分析两个函数的定义域和对应关系分别相同,值域一定相同吗?由此你对函数的三要素有什么新的认识?函数相等的条件:
如果两个函数的定义域和对应关系分别相同,那么它们的值 域一定相等.因此只要两个函数的定义域和对应关系分别相同,那 么这两个函数就相等.变式答案:-1小结:本节学了哪些内容?
(1)复习了函数的概念,总结了函数的三要素;
(2)学习了复合函数的概念;
(3)判断两个函数是否是同一个函数. 1.2.2函数的表示法(第一课时) 语言是沟通人与人之间的联系的,同样的祝福又有着不同的表示方法.例如,简体中文中的“生日快乐!”用繁体中文为:生日快樂!英文为:Happy Birthday!法文是Bon Anniversaire!德文是Alles Gute Zum Geburtstag!西班牙中称iFeliz CumpleaRos!印度尼西亚文是Selamat Ulang Tahun!荷兰文的生日快乐为Van Harte Gefeliciteerd met jeverj aardag!在俄语中则是С днем рождения!……
问题1:对于函数,又有什么不同的表示方法呢?引出课题——函数的表示法问题2:分析对比三种不同表示方法的优缺点?函数的三种表示方法:
解析法:用数学表达式表示两个变量之间的函数关系,这种表示方法叫做解析法,这个数学表达式叫做函数的解析式.
图象法:以自变量x的取值为横坐标,对应的函数值y为纵坐标,在平面直角坐标系中描出各个点,这些点构成了函数的图象,这种用图象表示两个变量之间函数关系的方法叫做图象法.
列表法:列一个两行多列的表格,第一行是自变量的取值,第二行是对应的函数值,这种用表格来表示两个变量之间的函数关系的方法叫做列表法.解析法能够准确表达出两个变量之间的关系,不足之处,比较抽象;图像形象直观表示两个变量之间的关系,不足之处,变量关系不够精确;列表法通过列表直观的得出两个变量的关系,不足之处,不能列出定义域为区间范围的函数,列表表示函数仅能表示有限个。例1.某种笔记本的单价是5元,买x(x∈{1,2,3,4,5})个笔记本需要y元,试用三种表示法表示函数y=f(x).4.车管站在某个星期日保管的自行车和电动车共有3 500辆次,其中电动车保管费是每辆一次0.5元,自行车保管费是每次一辆0.3元.
(1)若设自行车停放的辆次数为x,总的保管费收入为y元,试写出y关于x的函数关系式;
(2)若估计前来停放的3 500辆次自行车中,电动车的辆次不小于25%,但不大于40%,试求该保管站这个星期日收入保管费总数的范围.解:(1)由题意得
y=0.3x+0.5(3500-x)=-0.2x+1750,x∈N*且0≤x≤3500.
(2)若电动车的辆次不小于25%,但不大于40%,
则3500×(1-40%)≤x≤3 500×(1-25%),
即2100≤x≤2 625,
画出函数y=-0.2x+1750(2 100≤x≤2 625)的图象,可得
函数y=-0.2x+1750(2100≤x≤2625)的值域是[1225,1330],
即收入在1225元至1330元之间.小结
请同学们回想一下,这节课我们学了哪些函数的表示方法?在具体的实际问题中如何恰当地选择?
?作业
课本习题1.2A组7、8、9. 1.2.2函数的表示法(第二课时)问题1:当x>1时,f(x)=x+1;当x≤1时,f(x)=-x,请写出函数f(x)的解析式. 问题2:这个函数的解析式有什么特点?函数h(x)是分段函数,在定义域的不同部分,其解析式不同.2、分段函数是一个函数,不要把它误认为是几个函数问题4:分段函数是一个函数,那它的定义域和值域是什么?3、分段函数的定义域是各段定义域的并集,值域是各段值域的并集问题5:同学们能否举出生活中用分段函数描述的实际问题?如出租车的计费、个人所得税纳税额等。1、分段函数的定义:指在定义域的不同部分,有不同对应法则的函数.例1.画出函数y=|x|的图象.小结:本节课我们学了哪些内容,请同学们进行回顾和总结.作业课本P25习题1.2 B组 3、4. 1.2.2函数的表示法(第三课时) 前面学习了函数的概念是:一般地,设A,B是两个非空数集,如果按照某种对应法则f,对于集合A中的每个元素x,在集合B中都有唯一的元素y和它对应.
(1)对于任意一个实数,在数轴上都有唯一的点与之对应.
(2)班级里的一位同学在教室都有唯一的坐位与之对应.
(3)对于任意的三角形,都有唯一确定的面积与之对应.
那么这些对应又有什么特点呢?
?这种对应称为映射.结论:
①集合A、B均为非空集合,并且集合A中的元素在集合B中都有唯一的元素与之对应.
②一般地,设A、B是两个非空的集合,如果按某一个确定的对应法则f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射.记作“f:A→B”.
如果集合A中的元素x对应集合B中元素y,那么集合A中的元素x叫集合B中元素y的原象,集合B中元素y叫集合A中的元素x的象.
③包含两层意思:一是必有一个;二是只有一个,也就是说有且只有一个的意思,即是一对一或多对一.
④函数是特殊的映射,映射是函数的推广.例1.下列哪些对应是从集合A到集合B的映射?
(1)A={P|P是数轴上的点},B=R,对应关系f:数轴上的点与它所代表的实数对应;
(2)A={P|P是平面直角坐标系中的点},B={(x,y)|x∈R,y∈R},对应关系f:平面直角坐标系中的点与它的坐标对应;
(3)A={三角形},B={x|x是圆},对应关系f:每一个三角形都对应它的内切圆;
(4)A={x|x是新华中学的班级},B={x|x是新华中学的学生},对应关系f:每一个班级都对应班里的学生.解:(1)是映射;(2)是映射;(3)是映射;
(4)不是映射.新华中学的每个班级对应其班内的多个学生,是一对多,不符合映射的定义.例2.下列对应是不是从集合A到集合B的映射,为什么?
(1)A=R,B={x∈R|x≥0},对应法则是“求平方”;
(2)A=R,B={x∈R|x>0},对应法则是“求平方”;
(3)A={x∈R|x>0},B=R,对应法则是“求平方根”;
(4)A={平面内的圆},B={平面内的矩形},对应法则是“作圆的内接矩形”.解:(1)是映射,因为A中的任何一个元素,在B中都能找到唯一的元素与之对应.
(2)不是从集合A到集合B的映射,因为A中的元素0,在集合B中没有对应的元素.
(3)不是从集合A到集合B的映射,因为任何正数的平方根都有两个值,即集合A中的任何元素,在集合B中都有两个元素与之对应.
(4)不是从集合A到集合B的映射.因为一个圆有无穷多个内接矩形,即集合A中任何一个元素在集合B中有无穷多个元素与之对应.例3.设f:A→B是A到B的一个映射,其中A=B={(x,y)|x,y∈R},f:(x,y)→(x-y,x+y),求:
(1)A中元素(-1,2)在B中对应的元素;
(2)在A中什么元素与B中元素(-1,2)对应?1.设映射f:x→-x2+2x是实数集R=M到实数集R=N的映射,若对于实数p∈N,在M中不存在原象,则实数p的取值范围是( )
A.(1,+∞) B.[1,+∞) C.(-∞,1) D.(-∞,1]分析:f(a)表示在对应法则f下a对应的象,g(a)表示在对应法则g下a对应的象.
由表1和表2,得f[g(1)]=f(4)=1,g[f(1)]=g(3)=1,g[f(2)]=g(4)=2,g[f(3)]=g(2)=3,g[f(4)]=g(1)=4,
则有f[g(1)]=g[f(1)]=1,
故选A.
答案:A3.设集合A={a,b,c},集合B=R,以下对应关系中,一定能建立集合A到集合B的映射的是( )
A.对集合A中的数开平方
B.对集合A中的数取倒数
C.对集合A中的数取算术平方根
D.对集合A中的数立方分析:当a<0时,对a开平方或取算术平方根均无意义,则A、C错;当a=0时,对a取倒数无意义,则B错;由于对任何实数都能立方,并且其立方仅有一个,所以对集合A中的数立方能建立映射,故选D.
答案:D小结
请同学们回想一下,这节课我们学了哪些内容?
