7.2 定义与命题 课件(20张PPT)
文档属性
| 名称 | 7.2 定义与命题 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 252.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 00:00:00 | ||
图片预览








文档简介
课件20张PPT。亲爱的同学们:
每一个生命在此起航!
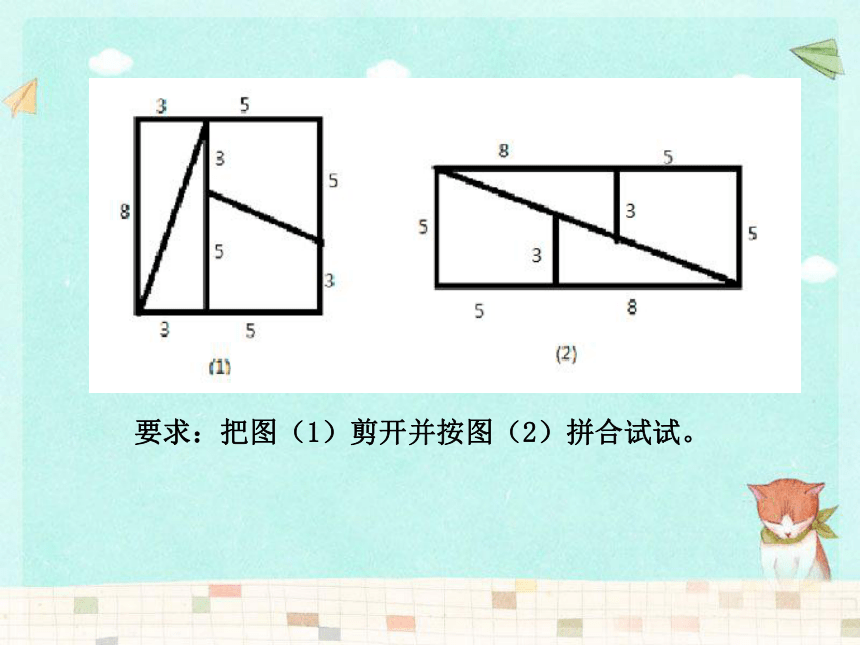
每一个梦想在此放飞!要求:把图(1)剪开并按图(2)拼合试试。12.1 定义与命题活动一
如:商店以比原来标价低的价格出售商品叫做 ; 打折“符号不同、绝对值相等的两个数”是 “ ”的定义;互为相反数对名称和术语的含义进行描述或做出规定,就是给出它们的定义.在同一平面内,不相交的两条直线是平行线.数轴上表示一个数的点到原点的距离称为这个数的绝对值.能使方程两边的值相等的未知数的值叫做方程的解.【说一说】活动二
(1)“等角的余角相等。”与“等角的余角相
等吗?”这两句话一样吗?
如果不一样,它们有什么不同?
(2)“经过一点有且只有一条直线与已知直线垂
直。”与“经过一点画已知直线的垂线。”
有什么不同?
(3)“四边形不是多边形。”与“四边形不一定是
多边形。”有什么不同?________________叫做命题.判断一件事情的句子下列句子是命题吗?【辨一辨】(1)若a2=4,求a 的值;
(2)如果a2=b2,那么a =b;
(3)两直线平行,同位角相等.
(4)a、b 两条直线平行吗?
(5)如果两个角的和是一个直角,那么这两个角互
为余角;
(6)如果∠DOE=2∠EOF,那么OF是∠DOE平分线.
(7)对顶角相等;
(8)画一个角等于已知角;
(9)直角三角形两个锐角互余.(2)如果a2=b2,那么a =b;
(3)两直线平行,同位角相等.
(5)如果两个角的和是一个直角,那么这两个角互
为余角;
(6)如果∠DOE=2∠EOF,那么OF是∠DOE平分线.
(7)对顶角相等;
(9)直角三角形两个锐角互余.活动三:
请你尝试把下列命题的进行合理分组?并说说理由。一组:
(2)如果a2=b2,那么a =b;
(5)如果两个角的和是一个直角,那么这两个角互
为余角;
(6)如果∠DOE=2∠EOF,那么OF是∠DOE平分线.另一组:
(3)两直线平行,同位角相等.
(7)对顶角相等;
(9)直角三角形两个锐角互余.
形式:“如果……,那么……。”简述命题 在数学中,命题一般可看作由条件和结论两部分组成,条件是已知事项,结论是由已知事项推出的事项. 【命题的结构】命题:如果a2=b2, 那么a =b;说出下列命题的条件和结论: (5)如果两个角的和是一个直角,那么这两个角互为余角; (6)如果∠DOE=2∠EOF,那么OF是∠DOE平分线. (3)两直线平行,同位角相等. 相等对顶角(两个角是)条件:(补上适当词语)结论:两个角(7)对顶角相等条件:两个角是对顶角,结论:这两个角相等.如果两个角是对顶角,那么这两个角相等. 改写:方法:
先结论,
后条件. (9)直角三角形两个锐角互余. 如果两个角是一个直角三角形的两个锐角, 那么这两个锐角互余。如果一个三角形是直角三角形,那么这个三角形的两个锐角互余。当一个命题写成“如果……那么……”的形式时,
“如果”后面是______,“那么”后面是______. 结论条件 归纳当一个命题不是“如果……那么……”的形式时,可以先将这个命题改成“如果……那么……”的形式,再找出命题的条件和结论.例:写出命题“对顶角相等”的条件和结论.解:将原命题改写成:“如果两个角是对顶角,那么这两个角相等”.所以命题的条件是“两个角是对顶角”,结论是“这两个角相等”.【辨一辨】:说出下列命题的条件和结论?
(1)如果a<0,b<0,那么a+b<0;
(2)两直线平行,同旁内角互补;
(3)有公共顶点的两个角是对顶角;
(4)π是无理数。
(3)两直线平行,同位角相等.
(5)如果两个角的和是一个直角,那么这两个角互为余角;
(7)对顶角相等;
(9)直角三角形两个锐角互余.(2)如果a2=b2,那么a =b;
(6)如果∠DOE=2∠EOF,那么OF是∠DOE平分线.
命题(3)、(5)、(7)、(9)都是正确的,也就是说,如果条件成立,那么结论成立.像这样的命题叫做真命题. 像命题(1)、(5),当条件成立时,不能保证结论总是正确的,也就是说结论不成立,这样的命题叫做假命题.判断下列命题中,哪些是真命题?哪些是假命题?
(1)相等的角是对顶角;
(2)内错角相等;
(3)大于90度的角是平角;
(4)如果a>b,b>c,那么a>c .
假命题假命题真命题假命题【辨一辨】过关检测:
判断下列句子是否是命题?若是命题说出它的条件和结论,并判断真假。
(1)延长线段AB到点C;
(2)两条直线相交,只有一个交点;
(3)同角的补角相等;
(4)任何数的平方都不小于0吗?
(5)垂直于同一条直线的两直线平行;
(6)用量角器画∠AOB=90°。
(7)直角都相等;
拓展与延伸
1.对于同一平面内的三条直线a,b,c给出下列五个论断:
(1)a∥b;(2)b∥c;(3)a⊥b;(4)a∥c;(5)a⊥c
以其中两个论断为条件,一个论断为结论,
组成一个正确的命题(至少写出3个)解:由(1)(2)得(4);
由(1)(4)得(2);
由(2)(4)得(1);
由(2)(3)得(5);
由(2)(5)得(3);
由(3)(5)得(2).
小结:1.通过今天的学习,你有什么收获?
2.还有什么疑问?爱因斯坦成功公式 :A=X+Y+Z
成功=正确方法+艰苦劳动+少说空话
如:商店以比原来标价低的价格出售商品叫做 ; 打折“符号不同、绝对值相等的两个数”是 “ ”的定义;互为相反数对名称和术语的含义进行描述或做出规定,就是给出它们的定义.在同一平面内,不相交的两条直线是平行线.数轴上表示一个数的点到原点的距离称为这个数的绝对值.能使方程两边的值相等的未知数的值叫做方程的解.【说一说】活动二
(1)“等角的余角相等。”与“等角的余角相
等吗?”这两句话一样吗?
如果不一样,它们有什么不同?
(2)“经过一点有且只有一条直线与已知直线垂
直。”与“经过一点画已知直线的垂线。”
有什么不同?
(3)“四边形不是多边形。”与“四边形不一定是
多边形。”有什么不同?________________叫做命题.判断一件事情的句子下列句子是命题吗?【辨一辨】(1)若a2=4,求a 的值;
(2)如果a2=b2,那么a =b;
(3)两直线平行,同位角相等.
(4)a、b 两条直线平行吗?
(5)如果两个角的和是一个直角,那么这两个角互
为余角;
(6)如果∠DOE=2∠EOF,那么OF是∠DOE平分线.
(7)对顶角相等;
(8)画一个角等于已知角;
(9)直角三角形两个锐角互余.(2)如果a2=b2,那么a =b;
(3)两直线平行,同位角相等.
(5)如果两个角的和是一个直角,那么这两个角互
为余角;
(6)如果∠DOE=2∠EOF,那么OF是∠DOE平分线.
(7)对顶角相等;
(9)直角三角形两个锐角互余.活动三:
请你尝试把下列命题的进行合理分组?并说说理由。一组:
(2)如果a2=b2,那么a =b;
(5)如果两个角的和是一个直角,那么这两个角互
为余角;
(6)如果∠DOE=2∠EOF,那么OF是∠DOE平分线.另一组:
(3)两直线平行,同位角相等.
(7)对顶角相等;
(9)直角三角形两个锐角互余.
形式:“如果……,那么……。”简述命题 在数学中,命题一般可看作由条件和结论两部分组成,条件是已知事项,结论是由已知事项推出的事项. 【命题的结构】命题:如果a2=b2, 那么a =b;说出下列命题的条件和结论: (5)如果两个角的和是一个直角,那么这两个角互为余角; (6)如果∠DOE=2∠EOF,那么OF是∠DOE平分线. (3)两直线平行,同位角相等. 相等对顶角(两个角是)条件:(补上适当词语)结论:两个角(7)对顶角相等条件:两个角是对顶角,结论:这两个角相等.如果两个角是对顶角,那么这两个角相等. 改写:方法:
先结论,
后条件. (9)直角三角形两个锐角互余. 如果两个角是一个直角三角形的两个锐角, 那么这两个锐角互余。如果一个三角形是直角三角形,那么这个三角形的两个锐角互余。当一个命题写成“如果……那么……”的形式时,
“如果”后面是______,“那么”后面是______. 结论条件 归纳当一个命题不是“如果……那么……”的形式时,可以先将这个命题改成“如果……那么……”的形式,再找出命题的条件和结论.例:写出命题“对顶角相等”的条件和结论.解:将原命题改写成:“如果两个角是对顶角,那么这两个角相等”.所以命题的条件是“两个角是对顶角”,结论是“这两个角相等”.【辨一辨】:说出下列命题的条件和结论?
(1)如果a<0,b<0,那么a+b<0;
(2)两直线平行,同旁内角互补;
(3)有公共顶点的两个角是对顶角;
(4)π是无理数。
(3)两直线平行,同位角相等.
(5)如果两个角的和是一个直角,那么这两个角互为余角;
(7)对顶角相等;
(9)直角三角形两个锐角互余.(2)如果a2=b2,那么a =b;
(6)如果∠DOE=2∠EOF,那么OF是∠DOE平分线.
命题(3)、(5)、(7)、(9)都是正确的,也就是说,如果条件成立,那么结论成立.像这样的命题叫做真命题. 像命题(1)、(5),当条件成立时,不能保证结论总是正确的,也就是说结论不成立,这样的命题叫做假命题.判断下列命题中,哪些是真命题?哪些是假命题?
(1)相等的角是对顶角;
(2)内错角相等;
(3)大于90度的角是平角;
(4)如果a>b,b>c,那么a>c .
假命题假命题真命题假命题【辨一辨】过关检测:
判断下列句子是否是命题?若是命题说出它的条件和结论,并判断真假。
(1)延长线段AB到点C;
(2)两条直线相交,只有一个交点;
(3)同角的补角相等;
(4)任何数的平方都不小于0吗?
(5)垂直于同一条直线的两直线平行;
(6)用量角器画∠AOB=90°。
(7)直角都相等;
拓展与延伸
1.对于同一平面内的三条直线a,b,c给出下列五个论断:
(1)a∥b;(2)b∥c;(3)a⊥b;(4)a∥c;(5)a⊥c
以其中两个论断为条件,一个论断为结论,
组成一个正确的命题(至少写出3个)解:由(1)(2)得(4);
由(1)(4)得(2);
由(2)(4)得(1);
由(2)(3)得(5);
由(2)(5)得(3);
由(3)(5)得(2).
小结:1.通过今天的学习,你有什么收获?
2.还有什么疑问?爱因斯坦成功公式 :A=X+Y+Z
成功=正确方法+艰苦劳动+少说空话
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
