7.3 平行线的判定 课件 (17张)
文档属性
| 名称 | 7.3 平行线的判定 课件 (17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 400.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 16:29:16 | ||
图片预览





文档简介
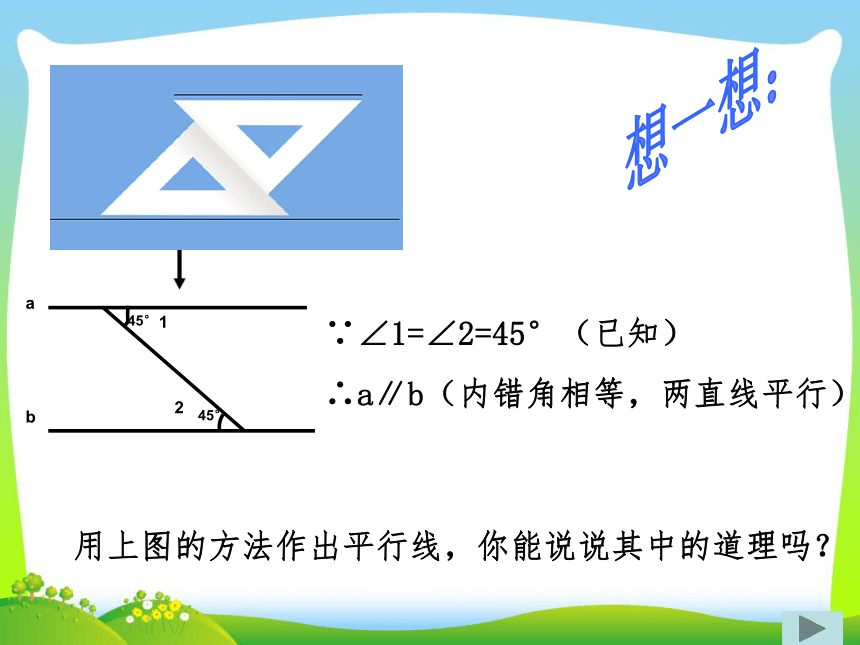
课件17张PPT。北师大版义务教育教科书数学八年级上册7.3平行线的判定入射光线DC与反射光线BA为什么平行呢?(一)创设情境,引入新课1.同位角相等,两直线平行2.内错角相等,两直线平行 (二)温故知新3.同旁内角互补,两直线平行前面,我们探索过两直线平行的哪些判别条件? (基本事实) 利用基本事实,证明:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.(三)证明定理,感受演绎 这一定理可简单写成:内错角相等,两直线平行.想一想:∵∠1=∠2=45°(已知)
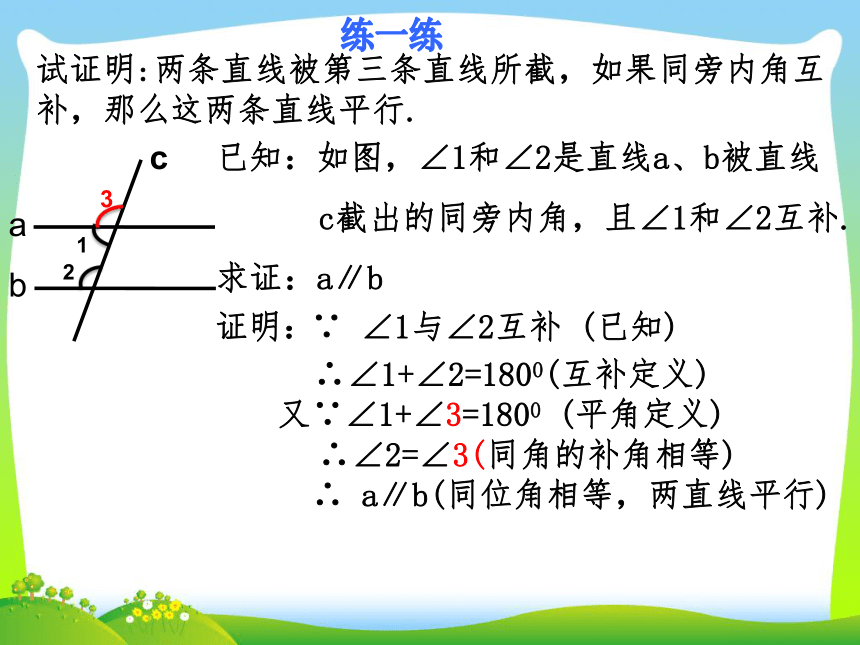
∴a∥b(内错角相等,两直线平行)用上图的方法作出平行线,你能说说其中的道理吗?试证明:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.已知:如图,∠1和∠2是直线a、b被直线
c截出的同旁内角,且∠1和∠2互补.
求证:a∥b证明:∵ ∠1与∠2互补 (已知) ∴∠1+∠2=1800(互补定义)又∵∠1+∠3=1800 (平角定义)∴∠2=∠3(同角的补角相等)∴ a∥b(同位角相等,两直线平行)练一练证明一个命题的一般步骤:(1)理解题意,弄清条件和结论,条件即是已知,结论即 是求证;(2)根据题意正确画出图形;(3)根据题意写出“已知”和“求证”;(4)分析题意,探索证明思路;总结反思(5)运用数学符号和数学语言,有条理、清晰地写出证明过程;(6)检查表达过程是否正确、完善.(四)课堂检测基础题
1.如图所示,若∠1=∠2,则 ∥ ;
若∠2=∠3,则 ∥ ,
理由是 .
′B同位角相等,两直线平行内错角相等,两直线平行.同旁内角互补,两直线平行.蜂房中的学问 蜂房的底部由三个全等的四边形围成,每个四边形的形状如图所示,其中∠α=109°28′,
∠β=70°32′.这样上下和左右都互相平行,就围成了我们日后要学习的平行四边形.
蜜蜂的本领 达尔文曾经说过:“(蜜蜂)巢房的精巧构造十分符合需要,如果一个人看到巢房而不倍加赞扬,那他一定是个糊涂虫。”这些小小的动物,它们用蜂蜡一昼夜可以造出几千间巢房。而且每间的体积几乎都是0.25立方厘米,壁厚都精确地保持在0.073±0.002毫米范围内。如果你仔细进行观察就会发现,每个巢房从正面看去都是正六边形(每个角都是120°),而它的尖顶形成的底部则都是由三个完全相同的菱形拼接而成的。十八世纪初,法国学者马拉而琪经过测量发现,所有的底部菱形的钝角都等于109°28′,而其锐角都等于70°32′。法国物理学家列奥缪拉由这个有趣的发现得到一个 启示:蜂房的这一特殊形状,可能是为了保证得到同样大的容积而所用材料最省。多么令人惊奇,小小的蜜蜂在人类有史以前就已经解决了的问题,十八世纪的数学家竟要用高等数学才能解决! 蜂房中有很多数学问题值得我们思考,有兴趣的同学可读一读华罗庚著:《谈谈与蜂房结构有关的数学问题》(科学出版社,2002.5)
连蜜蜂都把数学运用的这么好,你从中悟到了什么?
证明题
还记得开始时的小动画吗?当CM∥NB时,入射光线DC和反射光线BA为什么平行呢?简述理由.(∠1 =∠2,∠3=∠4)证明:∵ CM∥NB(已知)
∴ ∠3=∠2(两直线平行,内错角相等)
又∵ ∠3 =∠4,∠1=∠2(已知)
∴ ∠1 =∠2=∠3=∠4(等量代换)
∴ ∠1 +∠2=∠3+∠4(等式性质)
∴180°- (∠1 +∠2)= 180°-
( ∠3+∠4 )(等式性质)
即∠DCB= ∠ACB
∴CD ∥AB(内错角相等,两直线平行)同位角相等,两直线平行.或内错角相等,两直线平行.或同旁内角互补,两直线平行.(五)总结反思,拓展升华1.请同学们谈谈自己的收获.知识:
态度:
能力:
合作:
创新;
不足:
(自评或他评)变式1:如图②,已知:∠B+ ∠D =∠BCD ,求证:AB∥ED变式2:如图③,已知:∠D = ∠B+ ∠BCD ,求证:AB∥ED感谢光临指导!!
∴a∥b(内错角相等,两直线平行)用上图的方法作出平行线,你能说说其中的道理吗?试证明:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.已知:如图,∠1和∠2是直线a、b被直线
c截出的同旁内角,且∠1和∠2互补.
求证:a∥b证明:∵ ∠1与∠2互补 (已知) ∴∠1+∠2=1800(互补定义)又∵∠1+∠3=1800 (平角定义)∴∠2=∠3(同角的补角相等)∴ a∥b(同位角相等,两直线平行)练一练证明一个命题的一般步骤:(1)理解题意,弄清条件和结论,条件即是已知,结论即 是求证;(2)根据题意正确画出图形;(3)根据题意写出“已知”和“求证”;(4)分析题意,探索证明思路;总结反思(5)运用数学符号和数学语言,有条理、清晰地写出证明过程;(6)检查表达过程是否正确、完善.(四)课堂检测基础题
1.如图所示,若∠1=∠2,则 ∥ ;
若∠2=∠3,则 ∥ ,
理由是 .
′B同位角相等,两直线平行内错角相等,两直线平行.同旁内角互补,两直线平行.蜂房中的学问 蜂房的底部由三个全等的四边形围成,每个四边形的形状如图所示,其中∠α=109°28′,
∠β=70°32′.这样上下和左右都互相平行,就围成了我们日后要学习的平行四边形.
蜜蜂的本领 达尔文曾经说过:“(蜜蜂)巢房的精巧构造十分符合需要,如果一个人看到巢房而不倍加赞扬,那他一定是个糊涂虫。”这些小小的动物,它们用蜂蜡一昼夜可以造出几千间巢房。而且每间的体积几乎都是0.25立方厘米,壁厚都精确地保持在0.073±0.002毫米范围内。如果你仔细进行观察就会发现,每个巢房从正面看去都是正六边形(每个角都是120°),而它的尖顶形成的底部则都是由三个完全相同的菱形拼接而成的。十八世纪初,法国学者马拉而琪经过测量发现,所有的底部菱形的钝角都等于109°28′,而其锐角都等于70°32′。法国物理学家列奥缪拉由这个有趣的发现得到一个 启示:蜂房的这一特殊形状,可能是为了保证得到同样大的容积而所用材料最省。多么令人惊奇,小小的蜜蜂在人类有史以前就已经解决了的问题,十八世纪的数学家竟要用高等数学才能解决! 蜂房中有很多数学问题值得我们思考,有兴趣的同学可读一读华罗庚著:《谈谈与蜂房结构有关的数学问题》(科学出版社,2002.5)
连蜜蜂都把数学运用的这么好,你从中悟到了什么?
证明题
还记得开始时的小动画吗?当CM∥NB时,入射光线DC和反射光线BA为什么平行呢?简述理由.(∠1 =∠2,∠3=∠4)证明:∵ CM∥NB(已知)
∴ ∠3=∠2(两直线平行,内错角相等)
又∵ ∠3 =∠4,∠1=∠2(已知)
∴ ∠1 =∠2=∠3=∠4(等量代换)
∴ ∠1 +∠2=∠3+∠4(等式性质)
∴180°- (∠1 +∠2)= 180°-
( ∠3+∠4 )(等式性质)
即∠DCB= ∠ACB
∴CD ∥AB(内错角相等,两直线平行)同位角相等,两直线平行.或内错角相等,两直线平行.或同旁内角互补,两直线平行.(五)总结反思,拓展升华1.请同学们谈谈自己的收获.知识:
态度:
能力:
合作:
创新;
不足:
(自评或他评)变式1:如图②,已知:∠B+ ∠D =∠BCD ,求证:AB∥ED变式2:如图③,已知:∠D = ∠B+ ∠BCD ,求证:AB∥ED感谢光临指导!!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
