人教A版数学必修4 1.5 函数y=Asin(ωx+φ)的图象(共33张ppt)
文档属性
| 名称 | 人教A版数学必修4 1.5 函数y=Asin(ωx+φ)的图象(共33张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 958.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 00:00:00 | ||
图片预览








文档简介
课件33张PPT。 1.5函数y=Asin(ωx+j)的图象 在物理和工程技术的许多问题中,都要遇到形如y=Asin(ωx+φ)的函数(其中A,ω , φ是常数)。
如物体作简谐振动时位移S与时间T 的关系,交流电的电流y与时间x的关系,都可以用这一类的函数解析式来表示.
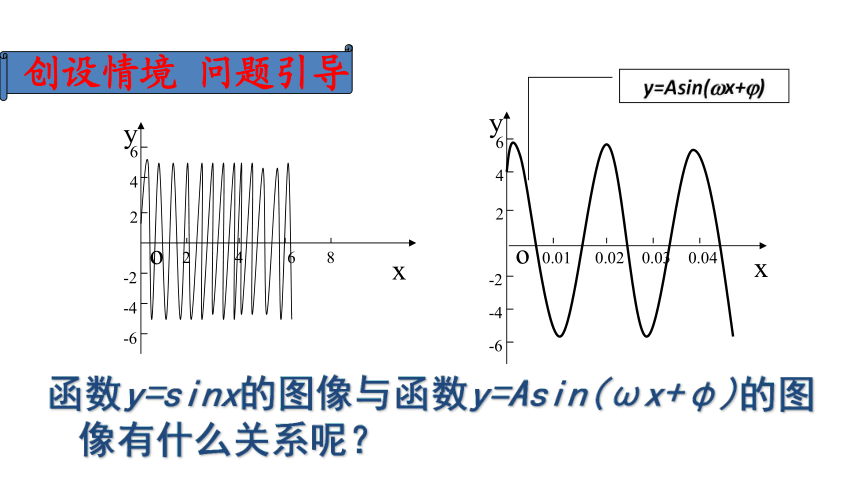
函数y=sinx的图像与函数y=Asin(ωx+φ)的图像有什么关系呢?
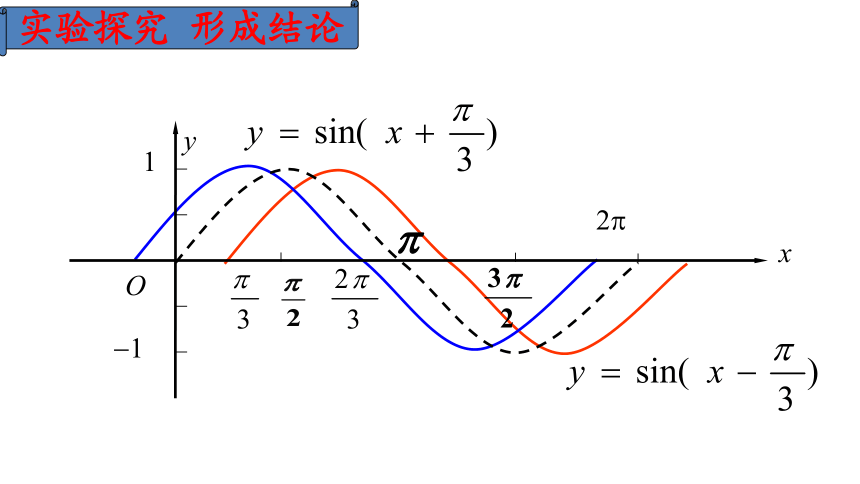
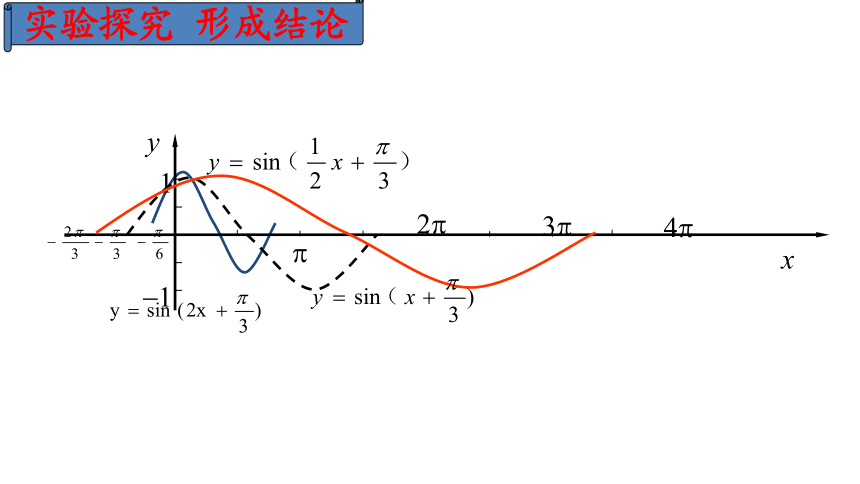
创设情境 问题引导y=Asin(?x+?)探索A,ω,φ对y=Asin(ωx+φ)的图象的影响.y=Asin(ωx+φ)(一)探索? 对 y=sin(x+? ), x∈R的图象的影响.实验探究 形成结论小结1: 一般地,函数y=sin(x+?),(?≠0)的图象,可以看作是把y=sinx的图象上所有的点向左(当?>0时)或向右(当?<0时)平行移动
|?|个单位而得到的。平移变换口答:如何由函数y=sinx的图象得到下列函数的图象?练习1(二)探索?对 y=sin(?x+? ), x∈R的图象的影响.实验探究 形成结论(二)探索?对 y=sin(?x+? ), x∈R的图象的影响.函数y=sin(?x+?)的图像可以看作是把y=sin(x+?)的图像上所有点的横坐标缩短(当?>1时)或伸长(0< ? <1时)到原来的 1/? 倍(纵坐标不变)而得到小结2 :周期变换(三)探索A对 y=Asin(?x+? ), x∈R的图象的影响.(三)探索A对 y=Asin(?x+? ), x∈R的图象的影响.函数y=Asin(?x+?)的图像可看作是把y=sin(?x+?)的图像上所有点的纵坐标伸长(当A>1时)或缩短 (0< A<1时)到原来的A倍(横坐标不变)而得到.小结3振幅变换函数y=Asin(? x+ ? )(其中A>0, ?>0)的图象如何由y=sinx得到?①先画出函数y=sinx的图象;
②再把正弦曲线向左(右)平移|?|个单位长度,得到函数y=sin(x+?)的图象;
③然后使曲线上各点的横坐标变为原来1/?倍,得到函数y=sin(?x+?)的图象;
④最后把曲线上各点的纵坐标变为原来的A倍,这时的曲线就是函数y=Asin(?x+?)的图象.先平移,后伸缩y=sin(x+φ)的图象
y=sin(ωx+φ)的图象y=Asin(ωx+φ)
的图象向左(φ>0)或向右(φ<0)平移︱φ︱个单位长度纵坐标伸长(A>1)或缩短(0的图象平移变换周期变换振幅变换先伸缩,后平移方法1:2??方法2:A 影响函数的最值;
? 影响函数的周期;
? 影响函数的位置.课堂小结:1、作正弦型函数y=Asin(?x+?) 的图象的方法:
(1)用“五点法”作图;
(2)利用变换关系作图。2、函数 y = sinx 的图象与函数 y=Asin(?x+?)的图象间的变换关系。3、余弦型函数 y=Acos(?x+?) 的相关问题同样处理。
y = sinx 的图象 y=Asin(?x+?)
Y = sin(?x+?)y=sin(x+?)y=sin ? x 当堂练习1:
如物体作简谐振动时位移S与时间T 的关系,交流电的电流y与时间x的关系,都可以用这一类的函数解析式来表示.
函数y=sinx的图像与函数y=Asin(ωx+φ)的图像有什么关系呢?
创设情境 问题引导y=Asin(?x+?)探索A,ω,φ对y=Asin(ωx+φ)的图象的影响.y=Asin(ωx+φ)(一)探索? 对 y=sin(x+? ), x∈R的图象的影响.实验探究 形成结论小结1: 一般地,函数y=sin(x+?),(?≠0)的图象,可以看作是把y=sinx的图象上所有的点向左(当?>0时)或向右(当?<0时)平行移动
|?|个单位而得到的。平移变换口答:如何由函数y=sinx的图象得到下列函数的图象?练习1(二)探索?对 y=sin(?x+? ), x∈R的图象的影响.实验探究 形成结论(二)探索?对 y=sin(?x+? ), x∈R的图象的影响.函数y=sin(?x+?)的图像可以看作是把y=sin(x+?)的图像上所有点的横坐标缩短(当?>1时)或伸长(0< ? <1时)到原来的 1/? 倍(纵坐标不变)而得到小结2 :周期变换(三)探索A对 y=Asin(?x+? ), x∈R的图象的影响.(三)探索A对 y=Asin(?x+? ), x∈R的图象的影响.函数y=Asin(?x+?)的图像可看作是把y=sin(?x+?)的图像上所有点的纵坐标伸长(当A>1时)或缩短 (0< A<1时)到原来的A倍(横坐标不变)而得到.小结3振幅变换函数y=Asin(? x+ ? )(其中A>0, ?>0)的图象如何由y=sinx得到?①先画出函数y=sinx的图象;
②再把正弦曲线向左(右)平移|?|个单位长度,得到函数y=sin(x+?)的图象;
③然后使曲线上各点的横坐标变为原来1/?倍,得到函数y=sin(?x+?)的图象;
④最后把曲线上各点的纵坐标变为原来的A倍,这时的曲线就是函数y=Asin(?x+?)的图象.先平移,后伸缩y=sin(x+φ)的图象
y=sin(ωx+φ)的图象y=Asin(ωx+φ)
的图象向左(φ>0)或向右(φ<0)平移︱φ︱个单位长度纵坐标伸长(A>1)或缩短(0
? 影响函数的周期;
? 影响函数的位置.课堂小结:1、作正弦型函数y=Asin(?x+?) 的图象的方法:
(1)用“五点法”作图;
(2)利用变换关系作图。2、函数 y = sinx 的图象与函数 y=Asin(?x+?)的图象间的变换关系。3、余弦型函数 y=Acos(?x+?) 的相关问题同样处理。
y = sinx 的图象 y=Asin(?x+?)
Y = sin(?x+?)y=sin(x+?)y=sin ? x 当堂练习1:
