2.2.2 向量的正交分解与向量的直角坐标运算 课件(20张)
文档属性
| 名称 | 2.2.2 向量的正交分解与向量的直角坐标运算 课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 625.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 09:18:40 | ||
图片预览





文档简介
(共20张PPT)
平面向量的坐标表示
目标:把平面内的任意向量用一有序实数对(坐标)表示
高一数学:必修四
复 习
1、平面向量基本定理的内容是什么?
2、什么是平面向量的基底?
平面向量的基本定理:
向量的基底:
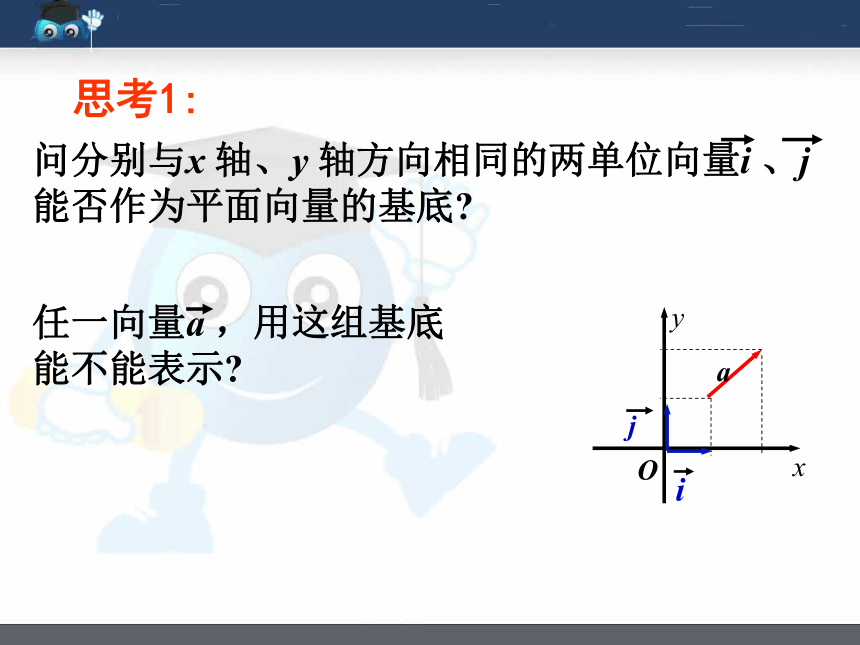
思考1:
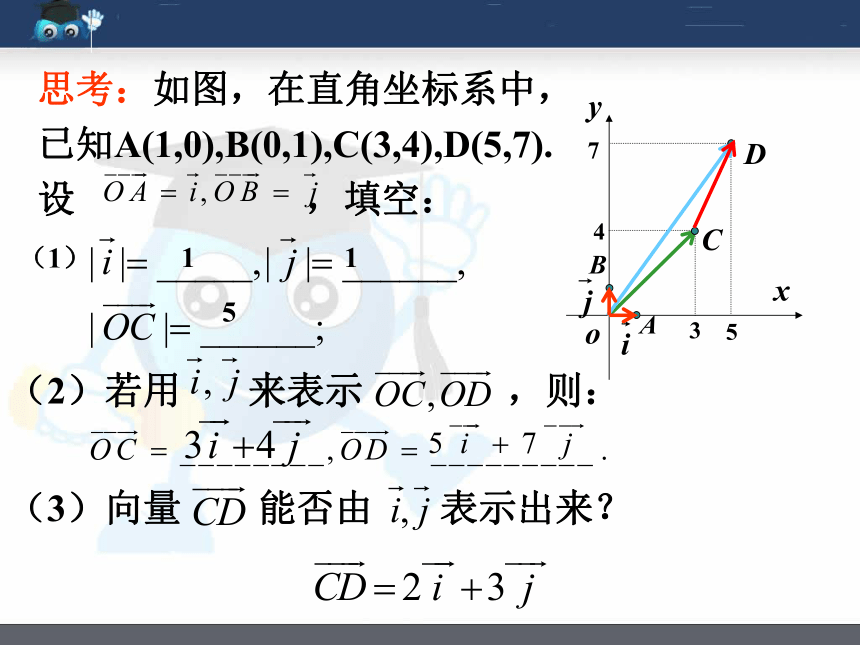
(1)
(2)若用 来表示 ,则:
1
1
5
3
5
4
7
(3)向量 能否由 表示出来?
平面向量的坐标表示
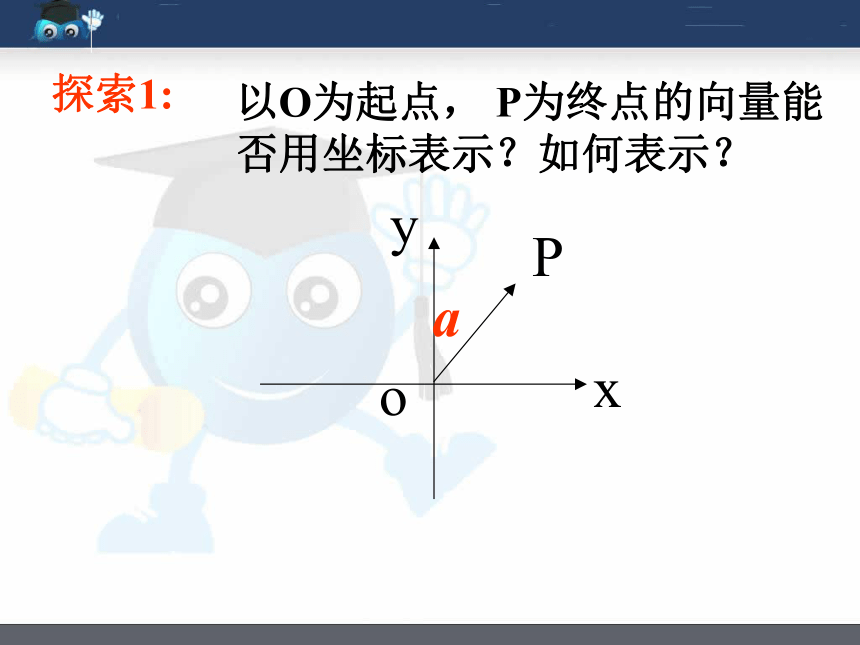
探索1:
以O为起点, P为终点的向量能否用坐标表示?如何表示?
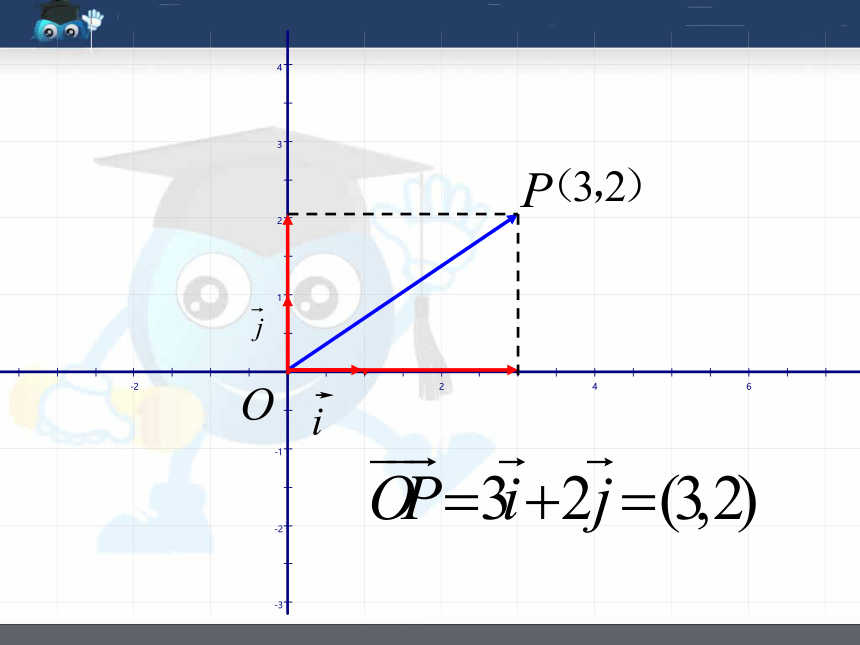
向量的坐标表示
在平面直角坐标系内,起点不在坐标原点O的向量如何用坐标来表示?
探索2:
A
o
x
y
可通过向量的平移,将向量的起点移到坐标的原点O处.
解决方案:
O
x
y
A
若a以O为起点,两者相同
思考:
2.两个向量相等的条件,利用坐标如何表示?
A
A1
A2
解:如图可知
同理
平面向量的坐标运算:
两个向量和(差)的坐标分别等于这两个
向量相应坐标的和(差)
实数与向量的积的坐标等于用这个实数乘原来向量的坐标
练习:已知
求 的坐标。
x
y
O
B
A
解:
一个向量的坐标等于表示此向量的
有向线段的终点的坐标减去起点的坐标。
这是一个重要结论!
例3.如图,已知 的三个顶点A、B、C的
坐标分别是(-2,1)、(-1,3)、(3,4),
试求顶点D的坐标。
解法1:设点D的坐标为(x,y)
解得 x=2,y=2
所以顶点D的坐标为(2,2)
课堂小结:
2 加、减法法则.
a + b=( x2 , y2) + (x1 ,? y1)= (x2+x1 , y2+y1)
3 实数与向量积的运算法则:
λa =λ(x i+y j )=λx i+λy j
4 向量坐标.
若A(x1 , y1) , B(x2 , y2)
1 向量坐标定义.
a - b=( x2 , y2) - (x1 ,? y1)= (x2- x1 , y2-y1)
平面向量的坐标表示
目标:把平面内的任意向量用一有序实数对(坐标)表示
高一数学:必修四
复 习
1、平面向量基本定理的内容是什么?
2、什么是平面向量的基底?
平面向量的基本定理:
向量的基底:
思考1:
(1)
(2)若用 来表示 ,则:
1
1
5
3
5
4
7
(3)向量 能否由 表示出来?
平面向量的坐标表示
探索1:
以O为起点, P为终点的向量能否用坐标表示?如何表示?
向量的坐标表示
在平面直角坐标系内,起点不在坐标原点O的向量如何用坐标来表示?
探索2:
A
o
x
y
可通过向量的平移,将向量的起点移到坐标的原点O处.
解决方案:
O
x
y
A
若a以O为起点,两者相同
思考:
2.两个向量相等的条件,利用坐标如何表示?
A
A1
A2
解:如图可知
同理
平面向量的坐标运算:
两个向量和(差)的坐标分别等于这两个
向量相应坐标的和(差)
实数与向量的积的坐标等于用这个实数乘原来向量的坐标
练习:已知
求 的坐标。
x
y
O
B
A
解:
一个向量的坐标等于表示此向量的
有向线段的终点的坐标减去起点的坐标。
这是一个重要结论!
例3.如图,已知 的三个顶点A、B、C的
坐标分别是(-2,1)、(-1,3)、(3,4),
试求顶点D的坐标。
解法1:设点D的坐标为(x,y)
解得 x=2,y=2
所以顶点D的坐标为(2,2)
课堂小结:
2 加、减法法则.
a + b=( x2 , y2) + (x1 ,? y1)= (x2+x1 , y2+y1)
3 实数与向量积的运算法则:
λa =λ(x i+y j )=λx i+λy j
4 向量坐标.
若A(x1 , y1) , B(x2 , y2)
1 向量坐标定义.
a - b=( x2 , y2) - (x1 ,? y1)= (x2- x1 , y2-y1)
