人教A版数学选修2—2 1.3.2 函数的极值与导数(共18张ppt)
文档属性
| 名称 | 人教A版数学选修2—2 1.3.2 函数的极值与导数(共18张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 234.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 09:20:48 | ||
图片预览




文档简介
课件18张PPT。1.3.2函数的极值与导数高二数学 选修2-2 第一章 导数及其应用学习目标:
1.理解极大值、极小值的概念;
2.能够运用判断极大值、极小值的方法来求函数的极值
3.掌握求可导函数的极值的步骤;
学习重点:
极大、极小值的判断方法,以及求函数的极值的步骤.
学习难点:
函数在某点取得极值的必要条件和充分条件 知识回顾:
1、函数的单调性与导数正负关系
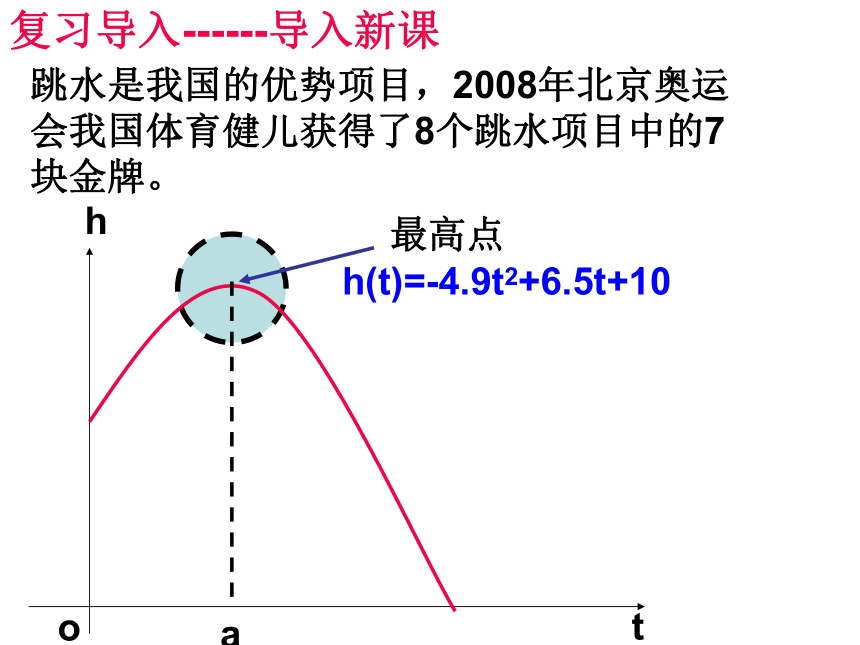
若f(x)在(a,b)内可导跳水是我国的优势项目,2008年北京奥运会我国体育健儿获得了8个跳水项目中的7块金牌。复习导入------导入新课h(t)=-4.9t2+6.5t+10一、复习导入----------导入新课单调递增
h ’(t)>0单调递减
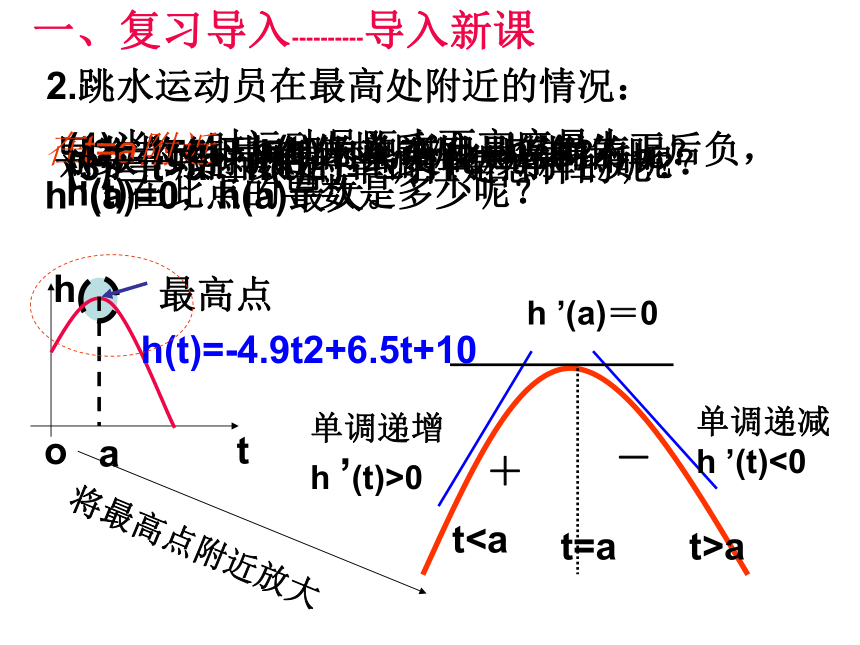
h ’(t)<0h ’(a)=02.跳水运动员在最高处附近的情况:(1)当t=a时运动员距水面高度最大,
h(t)在此点的导数是多少呢?(2)当ta时h(t)的单调性是怎样的呢?将最高点附近放大t=ata导数的符号有什么变化规律?在t=a附近,h(t)先增后减,h ’(t)先正后负,
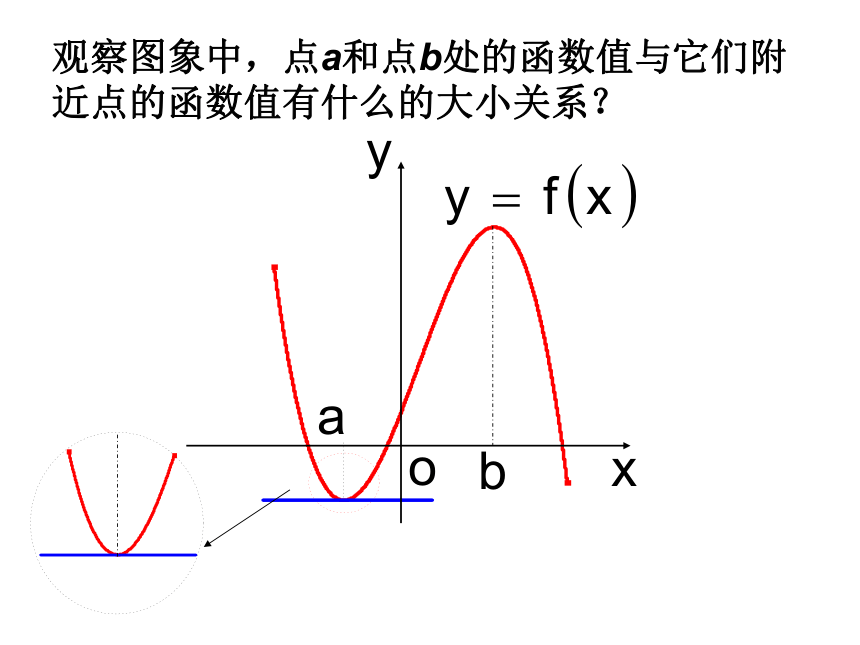
h ’(a)=0,h(a)最大。对于一般函数是否也有同样的性质呢?+-h(t)=-4.9t2+6.5t+10观察图象中,点a和点b处的函数值与它们附近点的函数值有什么的大小关系? 一般地,设函数f(x)在点a、b附近有定义,如果对a附近的所有的点,都有f(x)>f (a) ,我们就说f (a)是函数f(x)的一个极小值, 记作: f(x)极小值= f (a);一、函数极值的定义 如果对b附近的所有的点,都有f(x)记作: f(x)极大值=f (b). a叫做函数y=f(x)的极小值点.极大值与极小值统称为极值. b叫做函数y=f(x)的极大值点.1、极值是函数的最值吗,为什么?
2、极大值或极小值唯一吗?
3、极大值与极小值大小关系确定吗? Q(x2,f(x2))观察下列图像,结合极值定义思考以下问题: (1)极值是某一点附近的小区间而言 的,是函数的局部性质,不是整体的最值;
(2)函数在整个定义区间内可能有多个极值点,但定义域的端点绝不是极值点。
(3)极大值与极小值没有必然关系,极大值可能比极小值还小.
练习:y=f(x)的图像如图,找出f(x)的极大值点,极小值点c d e f o g h I j xy探究:极值点处导数值(即切线斜率)有何特点?c d e f o g h I j xy结论:极值点处,如果有切线,切线水平的.即: f ?(x)=0 f ?(x)<0x1极大值点两侧极小值点两侧 f ?(x)<0 f ?(x)>0 f ?(x)>0探究:极值点两侧导数正负符号有何规律?x2结论:变式练习: 下图是导函数 的图象, 试找出函数 的极值点, 并指出哪些是极大值点, 哪些是极小值点.abxyx1Ox2x3x4x5x6三、例题讲解求函数极值的一般步骤:
(1)确定函数的定义域
(2)求f(x)导数并求f’(x)=0的根
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)结论
所以,当x=-1时,函数的极大值是-2,当x=1时,函数的极小值是2极大值极小值小结通过本节课你学会了哪些知识?掌握了哪些技能?
1.极值、极值点的概念及取得极值的充分条件
2.掌握了求函数极值的方法及步骤
3.体会了数形结合解决问题的思想方法 ,解题过程中严谨的逻辑思维
1.理解极大值、极小值的概念;
2.能够运用判断极大值、极小值的方法来求函数的极值
3.掌握求可导函数的极值的步骤;
学习重点:
极大、极小值的判断方法,以及求函数的极值的步骤.
学习难点:
函数在某点取得极值的必要条件和充分条件 知识回顾:
1、函数的单调性与导数正负关系
若f(x)在(a,b)内可导跳水是我国的优势项目,2008年北京奥运会我国体育健儿获得了8个跳水项目中的7块金牌。复习导入------导入新课h(t)=-4.9t2+6.5t+10一、复习导入----------导入新课单调递增
h ’(t)>0单调递减
h ’(t)<0h ’(a)=02.跳水运动员在最高处附近的情况:(1)当t=a时运动员距水面高度最大,
h(t)在此点的导数是多少呢?(2)当t
h ’(a)=0,h(a)最大。对于一般函数是否也有同样的性质呢?+-h(t)=-4.9t2+6.5t+10观察图象中,点a和点b处的函数值与它们附近点的函数值有什么的大小关系? 一般地,设函数f(x)在点a、b附近有定义,如果对a附近的所有的点,都有f(x)>f (a) ,我们就说f (a)是函数f(x)的一个极小值, 记作: f(x)极小值= f (a);一、函数极值的定义 如果对b附近的所有的点,都有f(x)
2、极大值或极小值唯一吗?
3、极大值与极小值大小关系确定吗? Q(x2,f(x2))观察下列图像,结合极值定义思考以下问题: (1)极值是某一点附近的小区间而言 的,是函数的局部性质,不是整体的最值;
(2)函数在整个定义区间内可能有多个极值点,但定义域的端点绝不是极值点。
(3)极大值与极小值没有必然关系,极大值可能比极小值还小.
练习:y=f(x)的图像如图,找出f(x)的极大值点,极小值点c d e f o g h I j xy探究:极值点处导数值(即切线斜率)有何特点?c d e f o g h I j xy结论:极值点处,如果有切线,切线水平的.即: f ?(x)=0 f ?(x)<0x1极大值点两侧极小值点两侧 f ?(x)<0 f ?(x)>0 f ?(x)>0探究:极值点两侧导数正负符号有何规律?x2结论:变式练习: 下图是导函数 的图象, 试找出函数 的极值点, 并指出哪些是极大值点, 哪些是极小值点.abxyx1Ox2x3x4x5x6三、例题讲解求函数极值的一般步骤:
(1)确定函数的定义域
(2)求f(x)导数并求f’(x)=0的根
(3)用方程f’(x)=0的根,顺次将函数的定义域分成若干个开区间,并列成表格
(4)结论
所以,当x=-1时,函数的极大值是-2,当x=1时,函数的极小值是2极大值极小值小结通过本节课你学会了哪些知识?掌握了哪些技能?
1.极值、极值点的概念及取得极值的充分条件
2.掌握了求函数极值的方法及步骤
3.体会了数形结合解决问题的思想方法 ,解题过程中严谨的逻辑思维
