人教A版数学选修2—2 1.1.3 导数的几何意义(共25张ppt)
文档属性
| 名称 | 人教A版数学选修2—2 1.1.3 导数的几何意义(共25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 380.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 09:21:48 | ||
图片预览





文档简介
课件25张PPT。导数的几何意义一、教学内容一、说教材二、教学目标复习活动1 导数的定义:2 直线的斜率:3 已知直线上一点的坐标 ,且直线斜率为 ,则直线方程为: 创设情境问题一
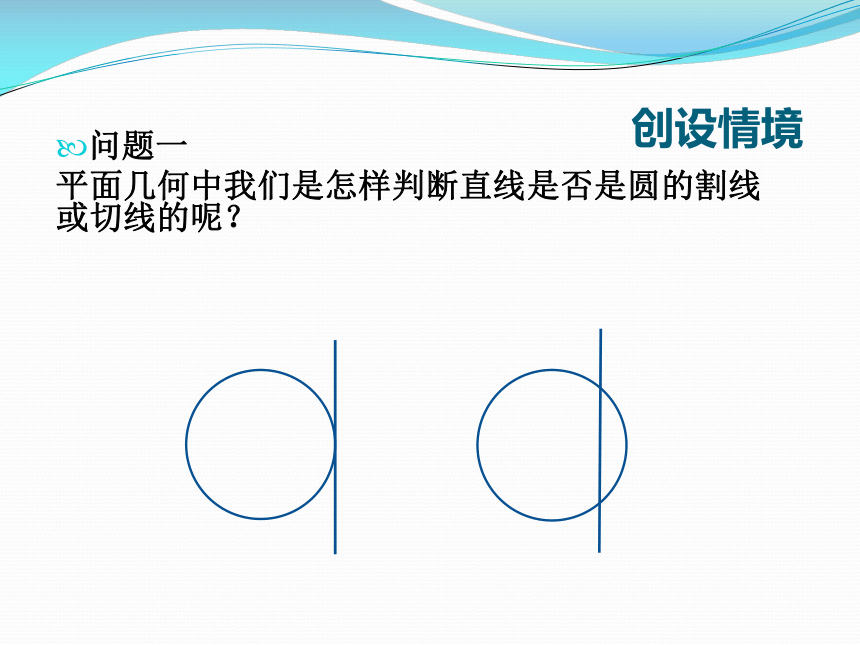
平面几何中我们是怎样判断直线是否是圆的割线或切线的呢?
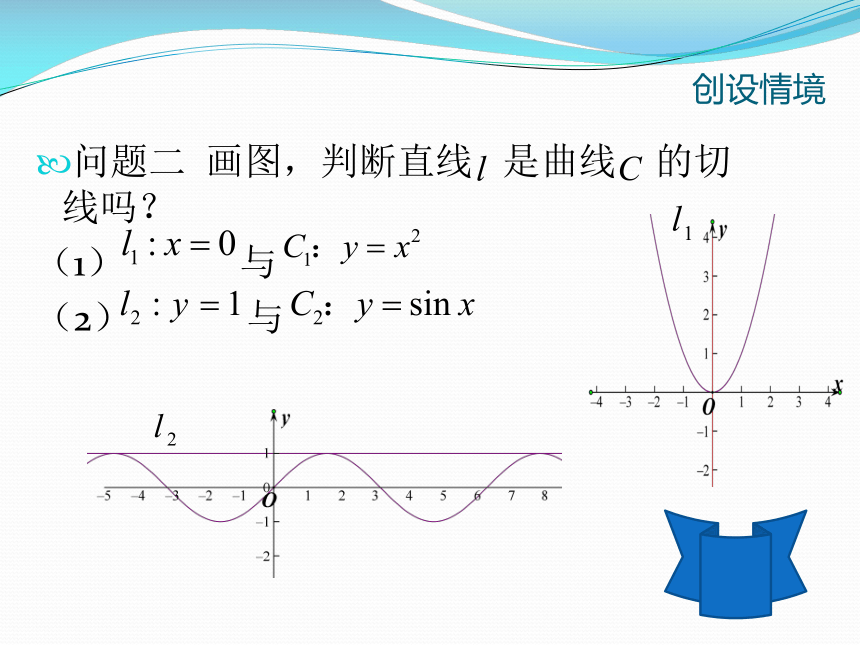
问题二 画图,判断直线 是曲线 的切线吗?
(1) 与
(2) 与创设情境平均变化率表示的是
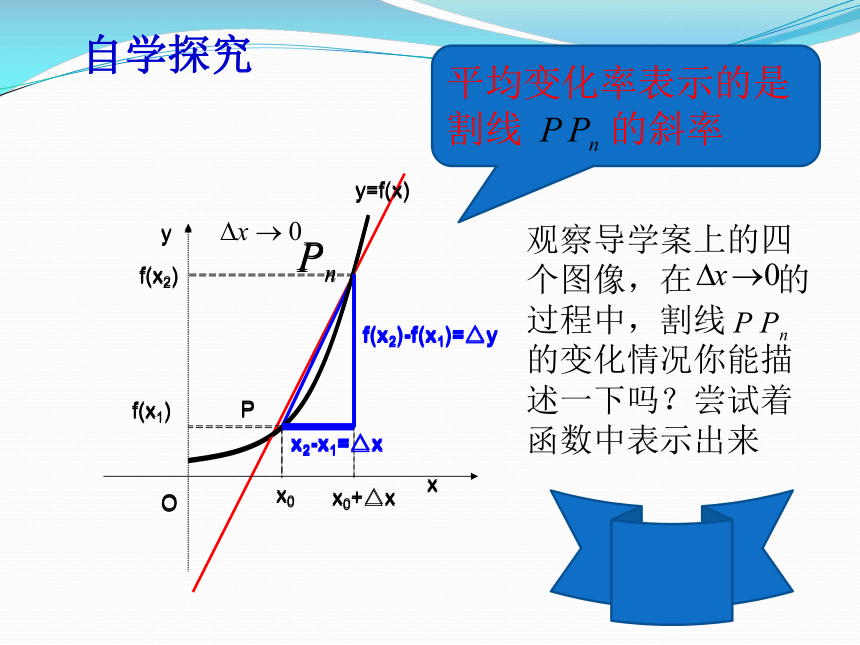
割线 的斜率观察导学案上的四个图像,在 的过程中,割线
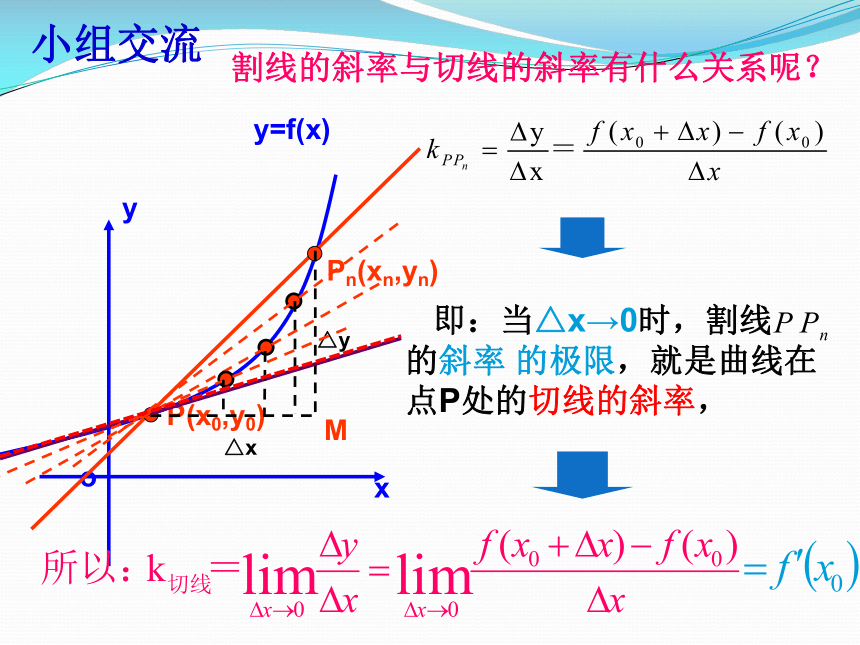
的变化情况你能描述一下吗?尝试着函数中表示出来自学探究M△x△y割线的斜率与切线的斜率有什么关系呢? 即:当△x→0时,割线 的斜率 的极限,就是曲线在点P处的切线的斜率, 小组交流二、导数的几何意义:函数 在 处的导数 的
几何意义就是:
(数形结合)探索求知曲线y=f(x)在点P(x0 ,f(x0)) 处的切线的斜率,就是函数 y=f(x)在点x0处的导数 故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:探究二:解决“问题二”圆的切线定义并不适用于一般的曲线。
而通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。探索求知根据导数的几何意义,在点P附近,曲线可以
用在点P处的切线近似代替 。探索求知数学上常用简单的对象来刻画复杂的对象。例如,用无理数3.1416近似代替无理数π。
这是微积分中重要的思想方法
---------以直代曲。知识运用解:先求 在 处的导数知识运用练习:(1)求函数y=3x2在点(1,3)处的导数.(2)求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.3.导函数函数 在点 处的导数 ,导函数 (导数)的区别与联系:(1)函数 在点处的导数是一个常数,不是变数.(2)函数的导数就是函数f(x)的导函数.的函数值,这也是求函数在点 处的导数的方法之一.
hto归纳总结求曲线在某点处的切线方程的基本步骤:
①求出P点的坐标;
②利用切线斜率的定义求出切线的斜率;
③利用点斜式求切线方程.知识运用课堂小结:(1)本节课你学到了什么?(2)本节课你理解了哪些数学思想方法?课堂小结:(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,即2.求切线方程的步骤:1.导数的几何意义3、数形结合、以直代曲的数学思想方法
平面几何中我们是怎样判断直线是否是圆的割线或切线的呢?
问题二 画图,判断直线 是曲线 的切线吗?
(1) 与
(2) 与创设情境平均变化率表示的是
割线 的斜率观察导学案上的四个图像,在 的过程中,割线
的变化情况你能描述一下吗?尝试着函数中表示出来自学探究M△x△y割线的斜率与切线的斜率有什么关系呢? 即:当△x→0时,割线 的斜率 的极限,就是曲线在点P处的切线的斜率, 小组交流二、导数的几何意义:函数 在 处的导数 的
几何意义就是:
(数形结合)探索求知曲线y=f(x)在点P(x0 ,f(x0)) 处的切线的斜率,就是函数 y=f(x)在点x0处的导数 故曲线y=f(x)在点P(x0 ,f(x0))处的切线方程是:探究二:解决“问题二”圆的切线定义并不适用于一般的曲线。
而通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。探索求知根据导数的几何意义,在点P附近,曲线可以
用在点P处的切线近似代替 。探索求知数学上常用简单的对象来刻画复杂的对象。例如,用无理数3.1416近似代替无理数π。
这是微积分中重要的思想方法
---------以直代曲。知识运用解:先求 在 处的导数知识运用练习:(1)求函数y=3x2在点(1,3)处的导数.(2)求曲线y=f(x)=x2+1在点P(1,2)处的切线方程.3.导函数函数 在点 处的导数 ,导函数 (导数)的区别与联系:(1)函数 在点处的导数是一个常数,不是变数.(2)函数的导数就是函数f(x)的导函数.的函数值,这也是求函数在点 处的导数的方法之一.
hto归纳总结求曲线在某点处的切线方程的基本步骤:
①求出P点的坐标;
②利用切线斜率的定义求出切线的斜率;
③利用点斜式求切线方程.知识运用课堂小结:(1)本节课你学到了什么?(2)本节课你理解了哪些数学思想方法?课堂小结:(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,即2.求切线方程的步骤:1.导数的几何意义3、数形结合、以直代曲的数学思想方法
