1.1.1 余弦定理 课件(19张PPT)
文档属性
| 名称 | 1.1.1 余弦定理 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 262.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-06 00:00:00 | ||
图片预览






文档简介
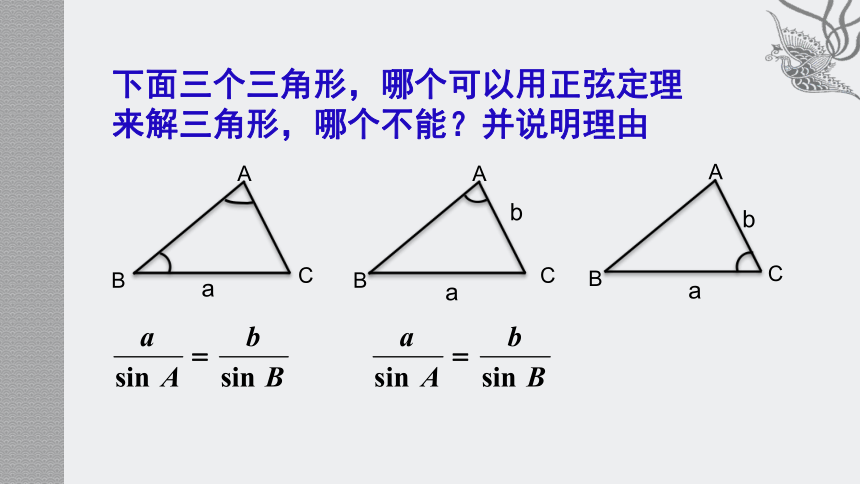
课件19张PPT。余 弦 定 理正弦定理:利用正弦定理可以解哪些类型的三角形:⑴ 已知两角和一边⑵ 已知两边和其中一边的对角 复习下面三个三角形,哪个可以用正弦定理
来解三角形,哪个不能?并说明理由学习目标:1、了解用几何法和向量法证明
余弦定理的过程;
2、能够从余弦定理得出其推论;
3、掌握用余弦定理及其推论来解
三角形,并判断三角形的形状。一、几何法已知:边a、边b、∠C,如何表示边c?当∠C为锐角时ABCacD当∠C为钝角时上述公式在直角三角形中是否还成立?当∠C为直角时勾股定理是余弦定理的特例,
余弦定理是勾股定理的推广。同理:二、向量法同理:余弦定理:三角形任何一边的平方等于其他两边的平方和
减去这两边与它们夹角的余弦的积的两倍。推论:探究一、利用余弦定理解三角形探究二、利用余弦定理判断三角形的形状∴△ABC是钝角三角形 ∵最大的∠C的余弦值为正数,
∴ ∠C是锐角,
∴ △ABC是锐角三角形已知三角形的三边,如何判断这个三角形的形状?如果三边同时出现,找出最大边(大边对大角)设a边为最大边,那么∠A就是最大角△ABC是钝角三角形△ABC是锐角三角形△ABC是直角三角形归纳:探究三、利用余弦定理进行边与角之间的转换∴ △ABC是等腰三角形还能用其他方法来判断此三角形的形状吗?方法二:用正弦定理探究四、应用余弦定理解决实际问题解:设t小时可以追上,∴甲船沿北偏东75°方向航行半个小时后追上乙船。1020t例4:甲船在海上A处发现了乙船在北偏东45°,且与A相距
10海里的C处,并且正以20海里/时的速度向南偏东75°的
方向航行。已知甲船的速度为 海里/时,问:甲船沿
什么方向,用多长时间可以追上乙船?本课小结:
余弦定理的作用:① 已知三角形的两边及夹角,求第三边,
进而求其他角② 已知三角形的三边求各角③ 利用余弦定理可以实现边角之间的转换
来解三角形,哪个不能?并说明理由学习目标:1、了解用几何法和向量法证明
余弦定理的过程;
2、能够从余弦定理得出其推论;
3、掌握用余弦定理及其推论来解
三角形,并判断三角形的形状。一、几何法已知:边a、边b、∠C,如何表示边c?当∠C为锐角时ABCacD当∠C为钝角时上述公式在直角三角形中是否还成立?当∠C为直角时勾股定理是余弦定理的特例,
余弦定理是勾股定理的推广。同理:二、向量法同理:余弦定理:三角形任何一边的平方等于其他两边的平方和
减去这两边与它们夹角的余弦的积的两倍。推论:探究一、利用余弦定理解三角形探究二、利用余弦定理判断三角形的形状∴△ABC是钝角三角形 ∵最大的∠C的余弦值为正数,
∴ ∠C是锐角,
∴ △ABC是锐角三角形已知三角形的三边,如何判断这个三角形的形状?如果三边同时出现,找出最大边(大边对大角)设a边为最大边,那么∠A就是最大角△ABC是钝角三角形△ABC是锐角三角形△ABC是直角三角形归纳:探究三、利用余弦定理进行边与角之间的转换∴ △ABC是等腰三角形还能用其他方法来判断此三角形的形状吗?方法二:用正弦定理探究四、应用余弦定理解决实际问题解:设t小时可以追上,∴甲船沿北偏东75°方向航行半个小时后追上乙船。1020t例4:甲船在海上A处发现了乙船在北偏东45°,且与A相距
10海里的C处,并且正以20海里/时的速度向南偏东75°的
方向航行。已知甲船的速度为 海里/时,问:甲船沿
什么方向,用多长时间可以追上乙船?本课小结:
余弦定理的作用:① 已知三角形的两边及夹角,求第三边,
进而求其他角② 已知三角形的三边求各角③ 利用余弦定理可以实现边角之间的转换
