2.1.2 数列的递推公式(选学) 课件(20张PPT)
文档属性
| 名称 | 2.1.2 数列的递推公式(选学) 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 253.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 09:42:49 | ||
图片预览



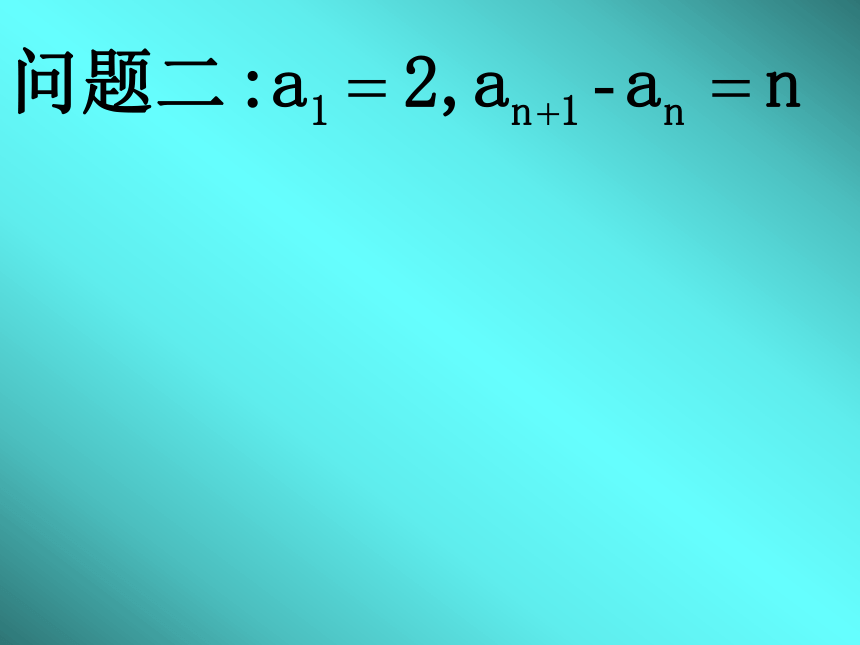




文档简介
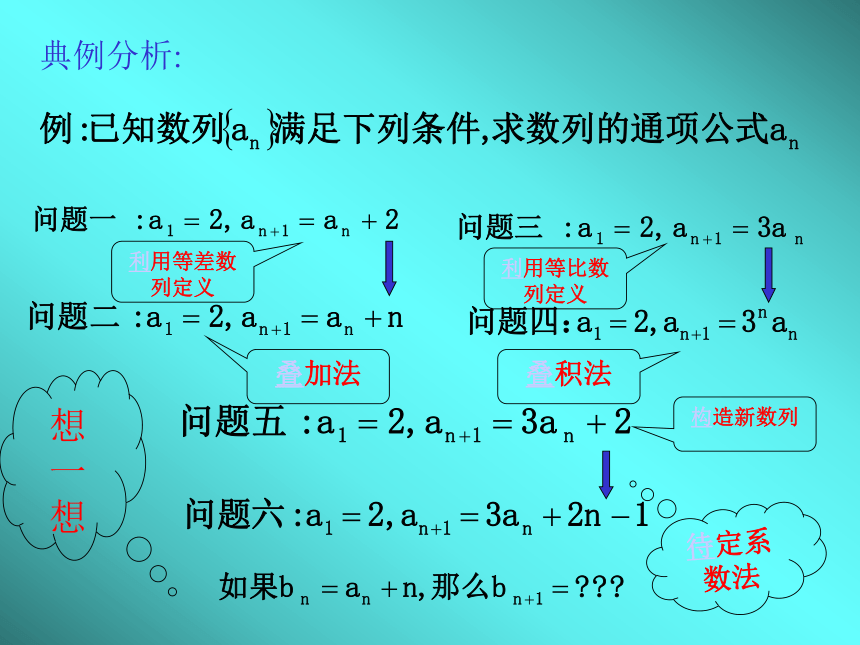
课件20张PPT。知识的获得是一个主动过程。教育学家布鲁纳说过: 由数列递推公式求通项典例分析:利用等差数列定义利用等比数列定义叠加法叠积法待定系数法想
一
想构造新数列解法一:解法二:利用叠加法各式累加得随堂练习1结论1.若数列{an}满足an+1-an=f(n) (n∈N+),
其中f(n)是可求和数列,那么可用叠加的方法求an。 其中f(n)可以是关于n的一次函数、二次函数、指数型函数、分式函数.
①若f(n)是关于n的一次函数,叠加后可转化为等差数列求和;
②若f(n)是关于n的二次函数,叠加后可分组求和;
③若f(n)是关于n的指型数函数,叠加后可转化为等比数列求和;
④若f(n)是关于n的分式函数,叠加后可裂项求和。备 注:解法一:解法二:叠积法各式叠积得结论若数列{an}满足 (n∈N+),其中
数列{f(n)}前 n项积可求,则其通项可采用叠积的方法求解。常见递推数列的通项公式的求法:课堂小结课后作业:谢谢大家!
一
想构造新数列解法一:解法二:利用叠加法各式累加得随堂练习1结论1.若数列{an}满足an+1-an=f(n) (n∈N+),
其中f(n)是可求和数列,那么可用叠加的方法求an。 其中f(n)可以是关于n的一次函数、二次函数、指数型函数、分式函数.
①若f(n)是关于n的一次函数,叠加后可转化为等差数列求和;
②若f(n)是关于n的二次函数,叠加后可分组求和;
③若f(n)是关于n的指型数函数,叠加后可转化为等比数列求和;
④若f(n)是关于n的分式函数,叠加后可裂项求和。备 注:解法一:解法二:叠积法各式叠积得结论若数列{an}满足 (n∈N+),其中
数列{f(n)}前 n项积可求,则其通项可采用叠积的方法求解。常见递推数列的通项公式的求法:课堂小结课后作业:谢谢大家!
