2.3.2 等比数列的前n项和 课件(25张PPT)
文档属性
| 名称 | 2.3.2 等比数列的前n项和 课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 09:50:35 | ||
图片预览






文档简介
课件25张PPT。21:2612.3.2等比数列的前n项和21:262复习:1.等比数列的定义:
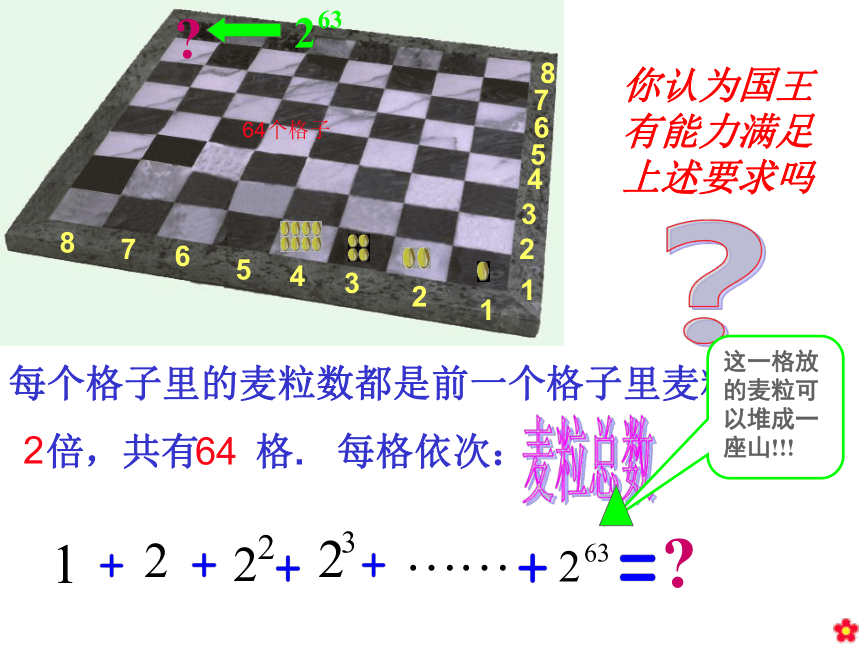
2.等比数列的通项公式:21:26364个格子1223344551667788OK456781567812334264个格子你认为国王有能力满足上述要求吗每个格子里的麦粒数都是前一个格子里麦粒数的
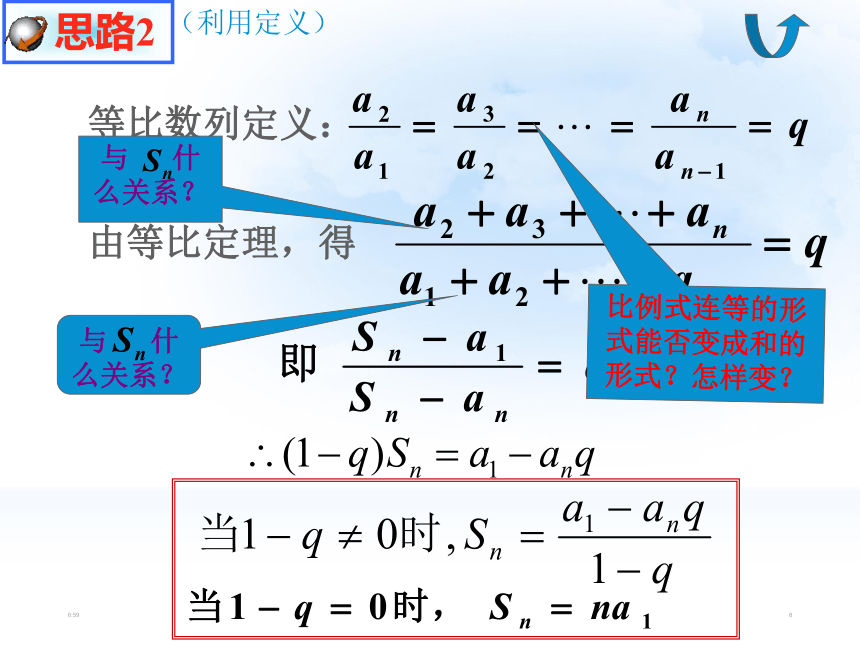
2倍,共有64格.麦粒总数???每格依次:21:2662.3.2 等比数列的前n项和21:267(错位相减法)当q≠1时两式相减,得当q=1时,Sn=?此式相邻两项有何关系?当q=1时 思路121:268(利用定义)由等比定理,得等比数列定义:与 什么关系?与 什么关系?比例式连等的形式能否变成和的形式?怎样变? 思路221:2691.注意q=1与q≠1两种情形2.q≠1时,3.五个量n、a1、q、an、Sn中,解决“知三求二”问题。 等比数列前n项和公式4.推导公式的方法:错位相减法。21:2610由刚才的例子可知:实际上就是一个以1为首项,2为公比的等比数列的前64项的求和问题,即: =18446744073709551615≈1.8421:2611 所以当人们把一袋一袋的麦子搬来开始计数时,国王才发现:就是把全印度甚至全世界的麦粒全拿来,也满足不了他的要求。其实,人们估计,全世界一千年也难以生产这么多麦子!是当时全世界在两千年内所产的小麦的总和! 假定千粒麦子的质量为40g,那么麦粒的总质量超过了7000亿吨。21:261221:261321:261421:2615n+1判断是非②n③①2n或0公式运用21:2616例1.“一尺之棰,日取其半,万世不竭”,怎样用学过的知识来说明它?解:这句古语来自《庄子 天下篇》,用现代文叙述是:
一尺长的木棒,每天取它的一半,永远也取不完。 如果每天取出的木棒的长度排成一个数列,则得到一个首项为a1= ,公比q= 的等比数列,21:2617它的前n项和为 不论n取何值, 总小于1, 这说明一尺长的木棒,每天取它的一半,永远也取不完。21:2618例2.等比数列{an}的公比q= ,a8=1,求它的前8项和S8。解1:因为a8=a1q7,所以 因此 21:2619解2:把原数列的第8项当作第一项,第1项当作第8项,
即顺序颠倒,也得到一个等比数列{bn},其中b1=a8=1,q’=2,所以前8项和 21:2620练习1. 根据下列条件,求相应的等比数列 的 练习21:2621例3.求和: 个分析:数列9,99,999,……,不是等比数列,不能直接用公式求和,
但将它转化为
10-1,100-1,1000-1,……,
就可以解决了。21:2622解:
原式=(10-1)+(100-1)+(1000-1)+…+(10n-1) =(10+100+1000+……+10n)-n21:2623解:
原式=(1-0.1)+(1-0.01)+(1-0.001)+…+(1-0.1n) =n -(0.1+0.01+0.001+……+0.1n)练习2. 计算: 0.9+0.99+0.999+···+0.999···9921:26241、求和公式当q≠1时,当q=1时,①注意分类讨论的思想:
等比数列求和时必须弄清q=1还是q≠1.②运用方程的思想,五个量“知三求二”.2、公式的推导方法 强调:错位相减法③注意运用整体运算的思想. 小结21:2625课后作业: 教材50页,A组:1. 2. 3
2.等比数列的通项公式:21:26364个格子1223344551667788OK456781567812334264个格子你认为国王有能力满足上述要求吗每个格子里的麦粒数都是前一个格子里麦粒数的
2倍,共有64格.麦粒总数???每格依次:21:2662.3.2 等比数列的前n项和21:267(错位相减法)当q≠1时两式相减,得当q=1时,Sn=?此式相邻两项有何关系?当q=1时 思路121:268(利用定义)由等比定理,得等比数列定义:与 什么关系?与 什么关系?比例式连等的形式能否变成和的形式?怎样变? 思路221:2691.注意q=1与q≠1两种情形2.q≠1时,3.五个量n、a1、q、an、Sn中,解决“知三求二”问题。 等比数列前n项和公式4.推导公式的方法:错位相减法。21:2610由刚才的例子可知:实际上就是一个以1为首项,2为公比的等比数列的前64项的求和问题,即: =18446744073709551615≈1.8421:2611 所以当人们把一袋一袋的麦子搬来开始计数时,国王才发现:就是把全印度甚至全世界的麦粒全拿来,也满足不了他的要求。其实,人们估计,全世界一千年也难以生产这么多麦子!是当时全世界在两千年内所产的小麦的总和! 假定千粒麦子的质量为40g,那么麦粒的总质量超过了7000亿吨。21:261221:261321:261421:2615n+1判断是非②n③①2n或0公式运用21:2616例1.“一尺之棰,日取其半,万世不竭”,怎样用学过的知识来说明它?解:这句古语来自《庄子 天下篇》,用现代文叙述是:
一尺长的木棒,每天取它的一半,永远也取不完。 如果每天取出的木棒的长度排成一个数列,则得到一个首项为a1= ,公比q= 的等比数列,21:2617它的前n项和为 不论n取何值, 总小于1, 这说明一尺长的木棒,每天取它的一半,永远也取不完。21:2618例2.等比数列{an}的公比q= ,a8=1,求它的前8项和S8。解1:因为a8=a1q7,所以 因此 21:2619解2:把原数列的第8项当作第一项,第1项当作第8项,
即顺序颠倒,也得到一个等比数列{bn},其中b1=a8=1,q’=2,所以前8项和 21:2620练习1. 根据下列条件,求相应的等比数列 的 练习21:2621例3.求和: 个分析:数列9,99,999,……,不是等比数列,不能直接用公式求和,
但将它转化为
10-1,100-1,1000-1,……,
就可以解决了。21:2622解:
原式=(10-1)+(100-1)+(1000-1)+…+(10n-1) =(10+100+1000+……+10n)-n21:2623解:
原式=(1-0.1)+(1-0.01)+(1-0.001)+…+(1-0.1n) =n -(0.1+0.01+0.001+……+0.1n)练习2. 计算: 0.9+0.99+0.999+···+0.999···9921:26241、求和公式当q≠1时,当q=1时,①注意分类讨论的思想:
等比数列求和时必须弄清q=1还是q≠1.②运用方程的思想,五个量“知三求二”.2、公式的推导方法 强调:错位相减法③注意运用整体运算的思想. 小结21:2625课后作业: 教材50页,A组:1. 2. 3
