3.2 均值不等式 课件(23张PPT)
文档属性
| 名称 | 3.2 均值不等式 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 536.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 00:00:00 | ||
图片预览





文档简介
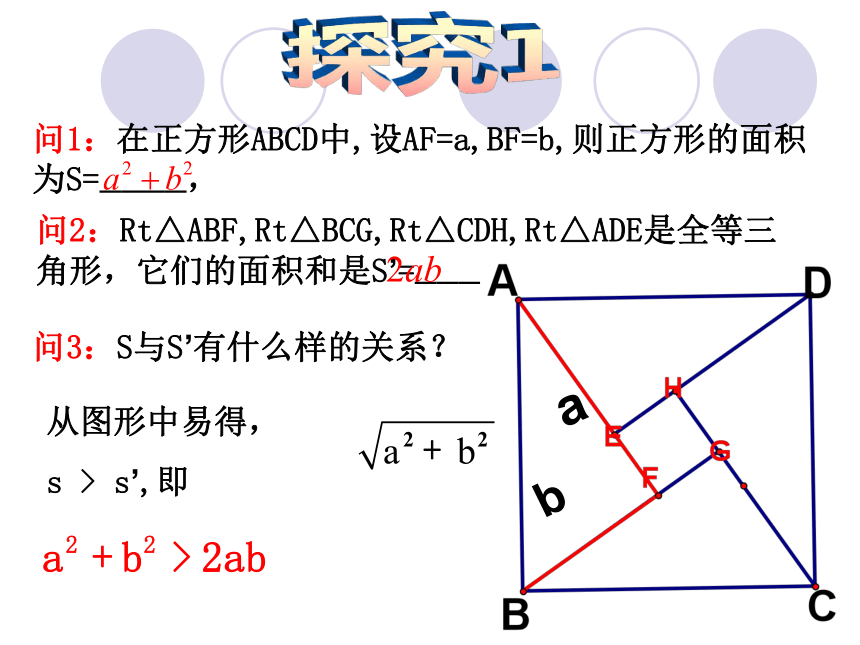
课件23张PPT。均值不等式2002年在北京举行的第24届国际数学家大会会标思考:这会标中含有怎样的几何图形?思考:你能否在这个图案中找出一些相等关系或不等关系?探究1ab问2:Rt△ABF,Rt△BCG,Rt△CDH,Rt△ADE是全等三角形,它们的面积和是S’=———问1:在正方形ABCD中,设AF=a,BF=b,则正方形的面积为S=————,问3:S与S’有什么样的关系? 从图形中易得,
s > s’,即探究1探究2
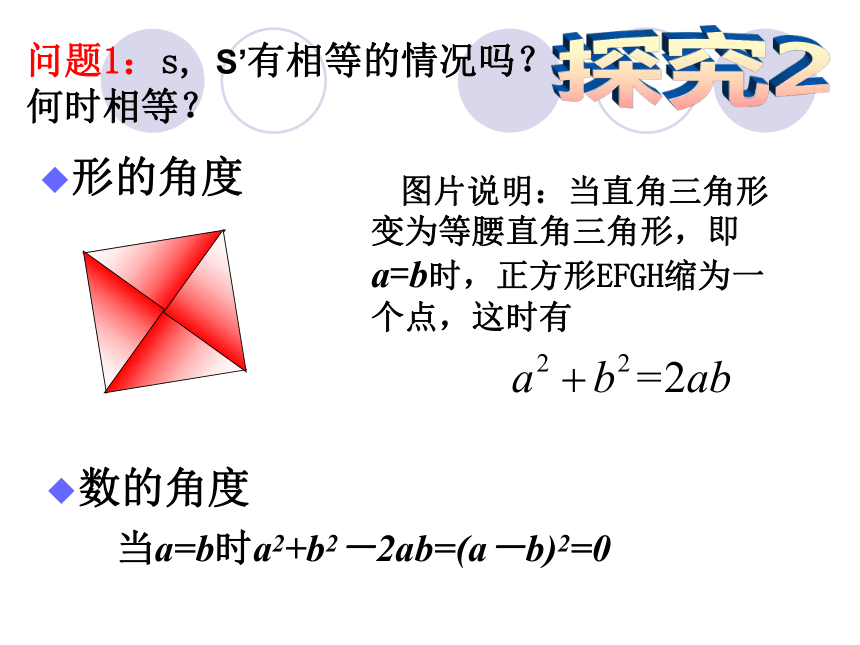
问题1:s, S’有相等的情况吗?何时相等? 图片说明:当直角三角形变为等腰直角三角形,即a=b时,正方形EFGH缩为一个点,这时有 形的角度数的角度当a=b时a2+b2-2ab=(a-b)2=0结论:一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立此不等式称为重要不等式探究2问题2:当 a,b为任意实数时, 成
立吗? 类 比 联 想 推 理 论 证 (特别的)如果
也可写成
a>0 ,b>0 ,
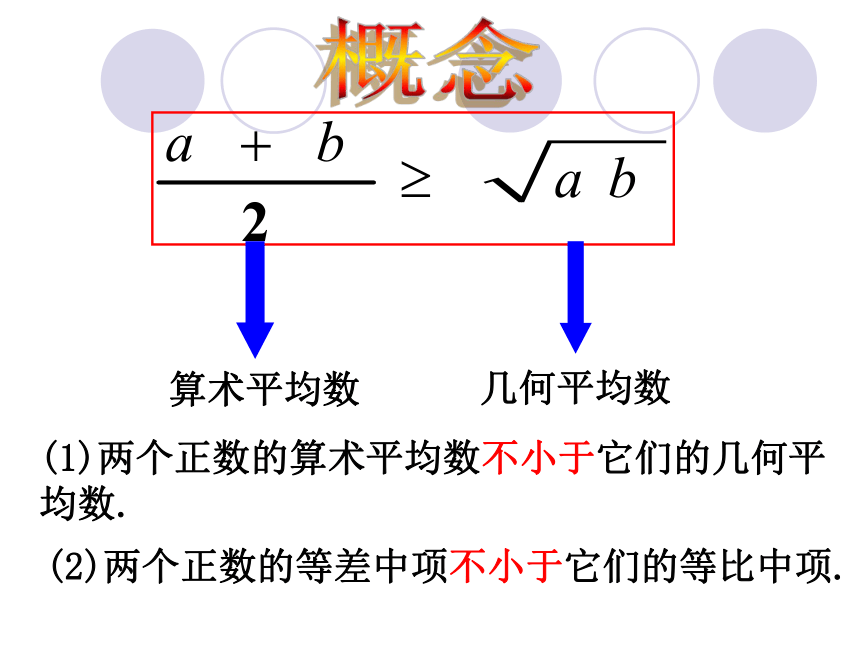
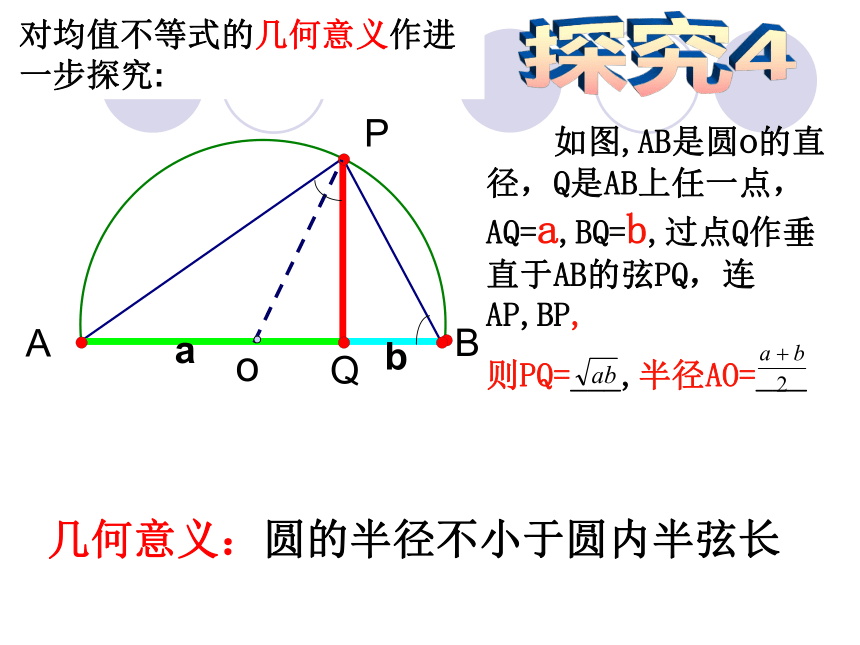
探究3概念(1)两个正数的算术平均数不小于它们的几何平 均数.(2)两个正数的等差中项不小于它们的等比中项.aboABPQ对均值不等式的几何意义作进一步探究: 如图,AB是圆o的直径,Q是AB上任一点,AQ=a,BQ=b,过点Q作垂直于AB的弦PQ,连AP,BP,
则PQ=___,半径AO=___几何意义:圆的半径不小于圆内半弦长探究4 已知 都是正数,试探究:
(1)如果积 是定值P,和 是否有最小值?若有,那么当 时,最小值为:
(2)如果和 是定值S,积 是否有最大值?若有,那么当 时,最大值为探究5例1:(1)用篱笆围成一个面积为100m的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短的篱笆是多少?
解:设矩形菜园的长为x m,宽为y m, 则xy=100,篱笆的长为2(x+y)m. 等号当且仅当x=y时成立,此时x=y=10. 因此,这个矩形的长、宽都为10m时,所用的篱笆最短,最短的篱笆是40m. 强调:两个正变量积为定值,则和有最小值,当且仅当两值相等时取最值。(2)用一段长为36m的篱笆围成一个矩形菜园,问这个矩形菜园的长和宽各为多少时,菜园的面积最大,最大面积是多少?解:设矩形菜园的长为xm,宽为ym, 则 2( x + y )= 36 , x + y = 18矩形菜园的面积为xym2=18/2=9得 xy 81当且仅当x=y,即x=y=9时,等号成立 因此,这个矩形的长、宽都为9m时,菜园面积最大,最大面积是81m2强调:两个正变量和为定值,则积有最大值,当且仅当两值相等时取最值。应用均值不等式求最值的条件:
a与b为正实数若等号成立,a与b必须能够相等一正二定三相等
积定和最小
和定积最大强调:求最值时要考虑不等式是否能取到“=”应用均值不等式求最值的条件:
a与b为正实数若等号成立,a与b必须能够相等一正二定三相等
积定和最小
和定积最大强调:求最值时要考虑不等式是否能取到“=”例2:某工厂要建造一个长方体形无盖贮水池,其容积为4800m3,深为3m.如果池底每平方米的造价为150元,池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?分析:水池呈长方体形,它的高是3m,底面的长与宽没有确定.如果底面的长与宽确定了,水池的总造价也就确定了.因此应当考察底面的长与宽取什么值时水池总造价最低。解:设底面的长为xm,宽为ym,水池总造价为z元.
根据题意,有:
由容积为4800m3,可得:3xy=4800
因此 xy=1600
由基本不等式与不等式的性质,可得
即
当x=y,即x=y=40时,等号成立
所以,将水池的地面设计成边长为40m的正方形时总造价最低,最低总造价为297600元.练一练1.下列函数中最小值为4的是( )
2.设a>1,且m=loga(a2+1),n=loga(a+1),
p=loga(2a)则m,n,p的大小关系是( )3.若a.b∈R,且a+b=3,则2a+2b的最小值为( )Cm>p>n4.设计一副宣传画,要求画面面积为4840cm2,画面的宽与高的比为a(a<1),画面的上下各留出8cm的空白,左右各留5cm的空白,怎样确定画面的高与宽的尺寸,能使宣传画所用纸张面积最小?解:设宣传画的宽为xcm,面积为S5.某种生产设备购买时费用为10万元,每年的设备管理费共计9千元,这种生产设备的维修费各年为:第一年2千元,第二年4千元,第三年6千元,依每年2千元的增量递增。问这种生产设备最多使用多少年报废最合算(即使用多少年的平均费用最少?)解:设使用x年报废最合算
1. 两个不等式
(1)
(2) 当且仅当a=b时,等号成立
注意:1.两公式条件,前者要求a,b为实数;后者要求a,b为正数。
2.公式的正向、逆向使用的条件以及“=”的成立条件。
2.不等式的简单应用:主要在于求最值
把握 “七字方针” 即 “一正,二定,三相等”课堂小结高考欣赏B略解:(4,6)A作业教材:P100:习题3.4A组
s > s’,即探究1探究2
问题1:s, S’有相等的情况吗?何时相等? 图片说明:当直角三角形变为等腰直角三角形,即a=b时,正方形EFGH缩为一个点,这时有 形的角度数的角度当a=b时a2+b2-2ab=(a-b)2=0结论:一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立此不等式称为重要不等式探究2问题2:当 a,b为任意实数时, 成
立吗? 类 比 联 想 推 理 论 证 (特别的)如果
也可写成
a>0 ,b>0 ,
探究3概念(1)两个正数的算术平均数不小于它们的几何平 均数.(2)两个正数的等差中项不小于它们的等比中项.aboABPQ对均值不等式的几何意义作进一步探究: 如图,AB是圆o的直径,Q是AB上任一点,AQ=a,BQ=b,过点Q作垂直于AB的弦PQ,连AP,BP,
则PQ=___,半径AO=___几何意义:圆的半径不小于圆内半弦长探究4 已知 都是正数,试探究:
(1)如果积 是定值P,和 是否有最小值?若有,那么当 时,最小值为:
(2)如果和 是定值S,积 是否有最大值?若有,那么当 时,最大值为探究5例1:(1)用篱笆围成一个面积为100m的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短的篱笆是多少?
解:设矩形菜园的长为x m,宽为y m, 则xy=100,篱笆的长为2(x+y)m. 等号当且仅当x=y时成立,此时x=y=10. 因此,这个矩形的长、宽都为10m时,所用的篱笆最短,最短的篱笆是40m. 强调:两个正变量积为定值,则和有最小值,当且仅当两值相等时取最值。(2)用一段长为36m的篱笆围成一个矩形菜园,问这个矩形菜园的长和宽各为多少时,菜园的面积最大,最大面积是多少?解:设矩形菜园的长为xm,宽为ym, 则 2( x + y )= 36 , x + y = 18矩形菜园的面积为xym2=18/2=9得 xy 81当且仅当x=y,即x=y=9时,等号成立 因此,这个矩形的长、宽都为9m时,菜园面积最大,最大面积是81m2强调:两个正变量和为定值,则积有最大值,当且仅当两值相等时取最值。应用均值不等式求最值的条件:
a与b为正实数若等号成立,a与b必须能够相等一正二定三相等
积定和最小
和定积最大强调:求最值时要考虑不等式是否能取到“=”应用均值不等式求最值的条件:
a与b为正实数若等号成立,a与b必须能够相等一正二定三相等
积定和最小
和定积最大强调:求最值时要考虑不等式是否能取到“=”例2:某工厂要建造一个长方体形无盖贮水池,其容积为4800m3,深为3m.如果池底每平方米的造价为150元,池壁每平方米的造价为120元,怎样设计水池能使总造价最低?最低总造价是多少?分析:水池呈长方体形,它的高是3m,底面的长与宽没有确定.如果底面的长与宽确定了,水池的总造价也就确定了.因此应当考察底面的长与宽取什么值时水池总造价最低。解:设底面的长为xm,宽为ym,水池总造价为z元.
根据题意,有:
由容积为4800m3,可得:3xy=4800
因此 xy=1600
由基本不等式与不等式的性质,可得
即
当x=y,即x=y=40时,等号成立
所以,将水池的地面设计成边长为40m的正方形时总造价最低,最低总造价为297600元.练一练1.下列函数中最小值为4的是( )
2.设a>1,且m=loga(a2+1),n=loga(a+1),
p=loga(2a)则m,n,p的大小关系是( )3.若a.b∈R,且a+b=3,则2a+2b的最小值为( )Cm>p>n4.设计一副宣传画,要求画面面积为4840cm2,画面的宽与高的比为a(a<1),画面的上下各留出8cm的空白,左右各留5cm的空白,怎样确定画面的高与宽的尺寸,能使宣传画所用纸张面积最小?解:设宣传画的宽为xcm,面积为S5.某种生产设备购买时费用为10万元,每年的设备管理费共计9千元,这种生产设备的维修费各年为:第一年2千元,第二年4千元,第三年6千元,依每年2千元的增量递增。问这种生产设备最多使用多少年报废最合算(即使用多少年的平均费用最少?)解:设使用x年报废最合算
1. 两个不等式
(1)
(2) 当且仅当a=b时,等号成立
注意:1.两公式条件,前者要求a,b为实数;后者要求a,b为正数。
2.公式的正向、逆向使用的条件以及“=”的成立条件。
2.不等式的简单应用:主要在于求最值
把握 “七字方针” 即 “一正,二定,三相等”课堂小结高考欣赏B略解:(4,6)A作业教材:P100:习题3.4A组
