3.5.1 二元一次不等式(组)所表示的平面区域 课件(21张PPT)
文档属性
| 名称 | 3.5.1 二元一次不等式(组)所表示的平面区域 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 00:00:00 | ||
图片预览






文档简介
课件21张PPT。3.5.1 二元一次不等式(组)
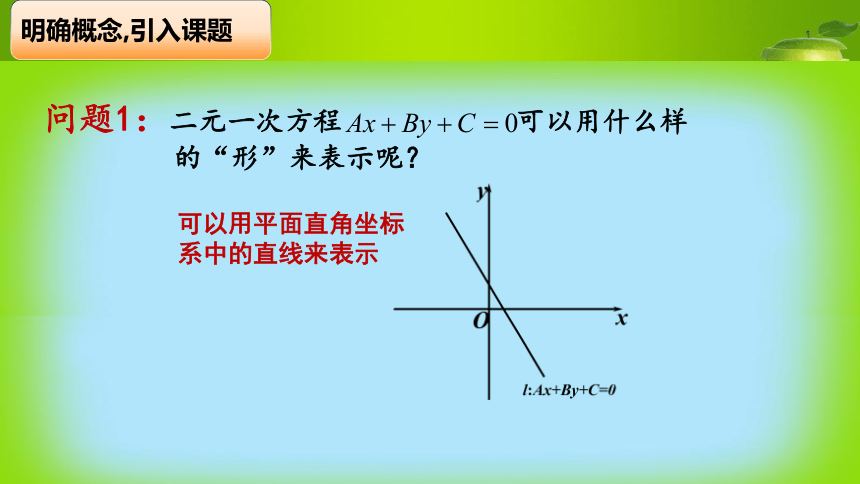
所表示的平面区域明确概念,引入课题可以用平面直角坐标
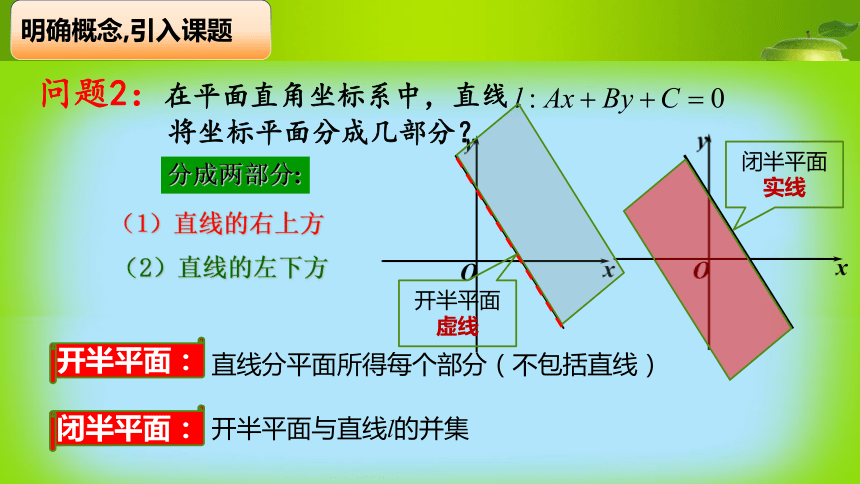
系中的直线来表示明确概念,引入课题分成两部分:(1)直线的右上方(2)直线的左下方开半平面:直线分平面所得每个部分(不包括直线)闭半平面:开半平面与直线l的并集开半平面
虚线闭半平面
实线明确概念,引入课题二元一次不等式二元一次不等式组观察四个不等式中,前两个不等式的共同特点是什么?1.都含有两个未知数
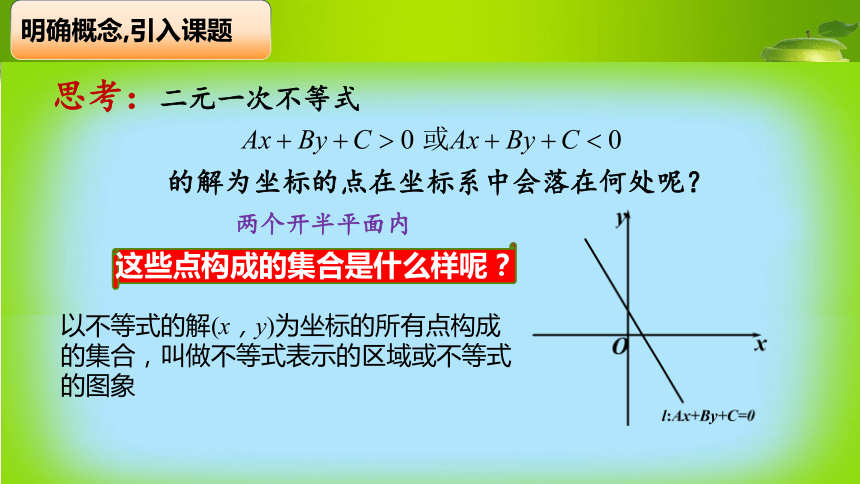
2.未知数的最高次数为1二元一次不等式(组)二元一次不等式的一般形式以不等式的解(x,y)为坐标的所有点构成的集合,叫做不等式表示的区域或不等式的图象这些点构成的集合是什么样呢?明确概念,引入课题两个开半平面内3.5.1 二元一次不等式(组) 所表示的平面区域特殊探究,发现规律探究1
(验证):直线l:x+y-1=0上的点的坐标满足x+y-1=0,那么直线两侧的点的坐标代入x+y-1中所得的值,与0什么关系?同侧、异侧有何规律呢?正负特殊探究,发现规律探究2(猜想):1.直线l右上方区域内的点(x,y),
使x +y-1____02.直线l左下方区域内的点(x, y),
使x +y-1____0x +y-1<0探究3(证明):P(x0,y0)(x,y)在直线 l 上任取一点P(x0,y0),过点P 作平行于 x 轴的直线 y=y0,在此直线上点P 右侧的任意一点(x,y) ,都有即同理猜想2也成立x +y-1>0反之,也成立特殊探究,发现规律2.如何确定不等式表示的是哪一个半平面区域?结论:1.同侧同号,异侧异号;
2.不等式表示的区域在一个半平面内推广论证,探究方法判断二元一次不等式表示的平面区域方法方法一:特殊点法2、点定域(代入特殊点验证)
特别地,当C≠0时,常把原点(0,0)作为特殊点.
当C=0时,常把点(1,0)作为特殊点.推广论证,探究方法判断二元一次不等式表示的平面区域方法点从直线上水平向左或右运动时,By+C为常值不变点向右运动时,x变大,z1变大,从而z值由z=0变为z>0,即则z1=Ax是增函数.同理,点向直线左侧运动,假设A>0,函数
思想推广论证,探究方法判断二元一次不等式表示的平面区域方法左方右方方法二:观察系数法①转化为A>0
②作出直线③定域典例精析,方法应用题型一:画二元一次不等式表示的区域画出不等式2x-y-3>0表示的平面区域.解:先画出直线2x-y-3=0 将原点(0,0)代入2x-y-3得
2?0-0-3=-3<0,
例1(画成虚线)所以不等式2x-y-3>0所表示的区域
是不包含原点的半平面.如图阴影部分
2x-y-3>0法2:利用x的系数A=2>0判断法1:注意:把直线画成虚线以表示区域不包括边界典例精析,方法应用题型一:画二元一次不等式表示的区域练一练画出不等式 表示的平面区域题型二:画二元一次不等式组表示的区域变式1?典例精析,方法应用题型二:画二元一次不等式组表示的区域
2x-y-3>0变式2典例精析,方法应用题型三:根据平面区域写出二元一次不等式(组)例2AC直线方程:BC直线方程:AB直线方程:课堂练习,强化巩固练习 不等式3x-4y+6<0表示的区域在直线3x-4y+6=0的( ) A.右上方 B.右下方 C.左上方 D.左下方
若点(1,2)和(1,1)在直线3x-y+m=0的异侧,则m的取值范围是_________C课堂小结 本节课我们学到了什么知识?1.二元一次不等式(组)表示的平面区域直线某一测所有点组成的平面区域各个不等式所表示的区域的公共部分2.确定平面区域的方法(1)特殊点法(2)观察系数法①直线定界(有等号画实线,无等号画虚线)②特殊点定域①化A为正②大(>)右小(<)左课后作业 教材P85 练习B第(1)题
P96 习题3-5
A组第1、2题
B组第1题
思考与讨论试证明B>0时:
(1)Ax+By+C>0表示直线Ax+By+C=0上方的部分;
(2)Ax+By+C<0表示直线Ax+By+C=0下方的部分.课后思考谢 谢 大 家
系中的直线来表示明确概念,引入课题分成两部分:(1)直线的右上方(2)直线的左下方开半平面:直线分平面所得每个部分(不包括直线)闭半平面:开半平面与直线l的并集开半平面
虚线闭半平面
实线明确概念,引入课题二元一次不等式二元一次不等式组观察四个不等式中,前两个不等式的共同特点是什么?1.都含有两个未知数
2.未知数的最高次数为1二元一次不等式(组)二元一次不等式的一般形式以不等式的解(x,y)为坐标的所有点构成的集合,叫做不等式表示的区域或不等式的图象这些点构成的集合是什么样呢?明确概念,引入课题两个开半平面内3.5.1 二元一次不等式(组) 所表示的平面区域特殊探究,发现规律探究1
(验证):直线l:x+y-1=0上的点的坐标满足x+y-1=0,那么直线两侧的点的坐标代入x+y-1中所得的值,与0什么关系?同侧、异侧有何规律呢?正负特殊探究,发现规律探究2(猜想):1.直线l右上方区域内的点(x,y),
使x +y-1____02.直线l左下方区域内的点(x, y),
使x +y-1____0x +y-1<0探究3(证明):P(x0,y0)(x,y)在直线 l 上任取一点P(x0,y0),过点P 作平行于 x 轴的直线 y=y0,在此直线上点P 右侧的任意一点(x,y) ,都有即同理猜想2也成立x +y-1>0反之,也成立特殊探究,发现规律2.如何确定不等式表示的是哪一个半平面区域?结论:1.同侧同号,异侧异号;
2.不等式表示的区域在一个半平面内推广论证,探究方法判断二元一次不等式表示的平面区域方法方法一:特殊点法2、点定域(代入特殊点验证)
特别地,当C≠0时,常把原点(0,0)作为特殊点.
当C=0时,常把点(1,0)作为特殊点.推广论证,探究方法判断二元一次不等式表示的平面区域方法点从直线上水平向左或右运动时,By+C为常值不变点向右运动时,x变大,z1变大,从而z值由z=0变为z>0,即则z1=Ax是增函数.同理,点向直线左侧运动,假设A>0,函数
思想推广论证,探究方法判断二元一次不等式表示的平面区域方法左方右方方法二:观察系数法①转化为A>0
②作出直线③定域典例精析,方法应用题型一:画二元一次不等式表示的区域画出不等式2x-y-3>0表示的平面区域.解:先画出直线2x-y-3=0 将原点(0,0)代入2x-y-3得
2?0-0-3=-3<0,
例1(画成虚线)所以不等式2x-y-3>0所表示的区域
是不包含原点的半平面.如图阴影部分
2x-y-3>0法2:利用x的系数A=2>0判断法1:注意:把直线画成虚线以表示区域不包括边界典例精析,方法应用题型一:画二元一次不等式表示的区域练一练画出不等式 表示的平面区域题型二:画二元一次不等式组表示的区域变式1?典例精析,方法应用题型二:画二元一次不等式组表示的区域
2x-y-3>0变式2典例精析,方法应用题型三:根据平面区域写出二元一次不等式(组)例2AC直线方程:BC直线方程:AB直线方程:课堂练习,强化巩固练习 不等式3x-4y+6<0表示的区域在直线3x-4y+6=0的( ) A.右上方 B.右下方 C.左上方 D.左下方
若点(1,2)和(1,1)在直线3x-y+m=0的异侧,则m的取值范围是_________C课堂小结 本节课我们学到了什么知识?1.二元一次不等式(组)表示的平面区域直线某一测所有点组成的平面区域各个不等式所表示的区域的公共部分2.确定平面区域的方法(1)特殊点法(2)观察系数法①直线定界(有等号画实线,无等号画虚线)②特殊点定域①化A为正②大(>)右小(<)左课后作业 教材P85 练习B第(1)题
P96 习题3-5
A组第1、2题
B组第1题
思考与讨论试证明B>0时:
(1)Ax+By+C>0表示直线Ax+By+C=0上方的部分;
(2)Ax+By+C<0表示直线Ax+By+C=0下方的部分.课后思考谢 谢 大 家
