3.5.2 简单线性规划 课件(28张PPT)
文档属性
| 名称 | 3.5.2 简单线性规划 课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 00:00:00 | ||
图片预览





文档简介
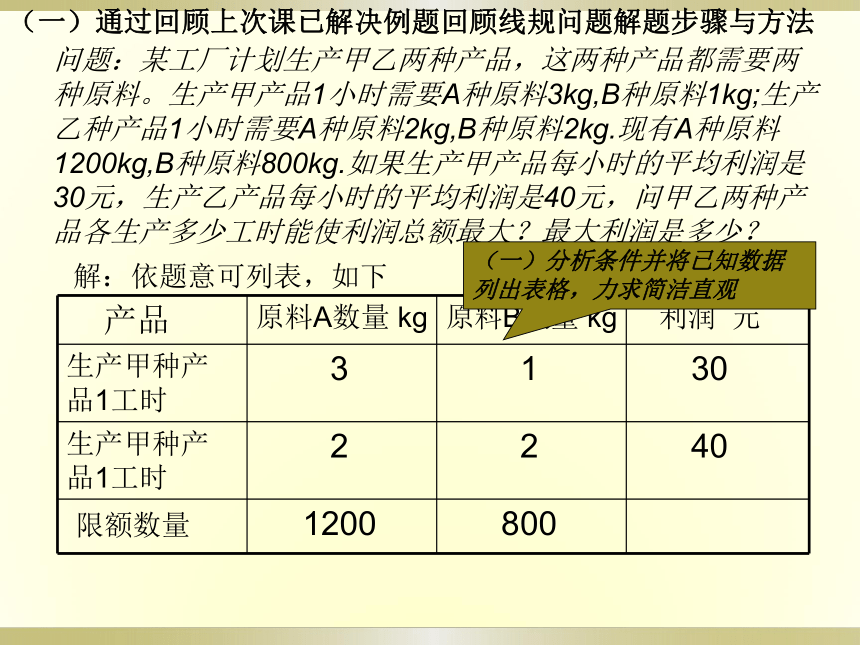
课件28张PPT。3.5.2简单线性规划(2)客房设置物资调动产品安排合理下料给定一定数量的人力,物力与资金资源,怎样运用资源使完成任务最大,收到的效益最大给定一项任务,怎样统筹安排,使完成这项任务消耗的人力物力资源最小问题:某工厂计划生产甲乙两种产品,这两种产品都需要两种原料。生产甲产品1小时需要A种原料3kg,B种原料1kg;生产乙种产品1小时需要A种原料2kg,B种原料2kg.现有A种原料1200kg,B种原料800kg.如果生产甲产品每小时的平均利润是30元,生产乙产品每小时的平均利润是40元,问甲乙两种产品各生产多少工时能使利润总额最大?最大利润是多少?解:依题意可列表,如下(一)分析条件并将已知数据列出表格,力求简洁直观(一)通过回顾上次课已解决例题回顾线规问题解题步骤与方法(2)设变量 x y,
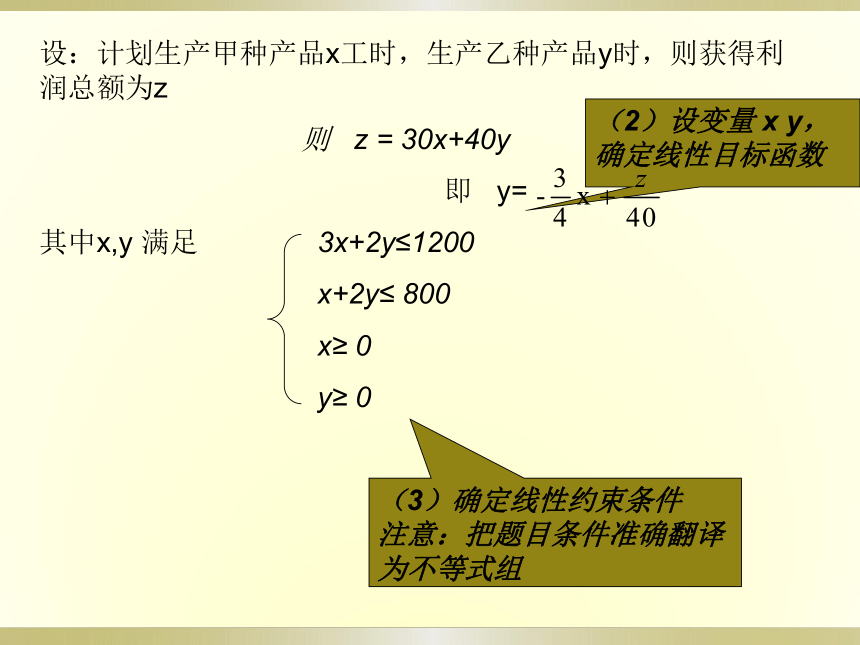
确定线性目标函数设:计划生产甲种产品x工时,生产乙种产品y时,则获得利润总额为z
则 z = 30x+40y
即 y=
其中x,y 满足 3x+2y≤1200
x+2y≤ 800
x≥ 0
y≥ 0
(3)确定线性约束条件
注意:把题目条件准确翻译为不等式组 解
3x+2y=1200
x+2y= 800
得 B(200,300)Zmax=30×200+40×300=18000L1:3x+2y-1200=0(4)画出可行域
①画线 ②定侧 ③求交(5)利用线性目标函数(直线)求出最优解平移3x+4y=0可知点B为最优解①变形 :由z=ax+by变为 y= -
求z的最值转化为求直线 y= 在y轴上的截距的最值。
(a,b是常数,z随x,y的变化而变化)
b>0时, 取最大值(或最小值)时z也取最大值(或
最小值);b< 0时, 取最大值,z取最小值。
取最小值时,z取最大值。
②平移:将ax+by=0平行移动,在可行域中,观察 截距 最大(或最小)时刚经过的点,即最优点
③求值:解有关方程组求出最优点的坐标,代入目标函数。求出目标函数的最值 下表给出甲乙丙三种食物中的维生素A、B的含量及单价营养师想购买这三种食物共10千克,使他们所含的维生素A不少于4400单位,维生素B不少于4800单位,而且要使付出的金额最低,这三种食物应各购买多少千克?例1食品配置解:设甲购买甲种食物x千克,乙种食物y千克,则购买丙种食物(10-x-y)千克。又设总支出为z元,依题意得 Z=7x+6y+5(10-x-y),
化简得z=2x+y+50.
x,y应满足的约束条件 400x+600y+400(10-x-y)≥ 4400
800x+200+400(10-x-y) ≥ 4800
x≥ 0 , y≥ 0
10-x-y≥ 0化简,得y ≥ 2
2x-y ≥ 4
X=y ≤ 10
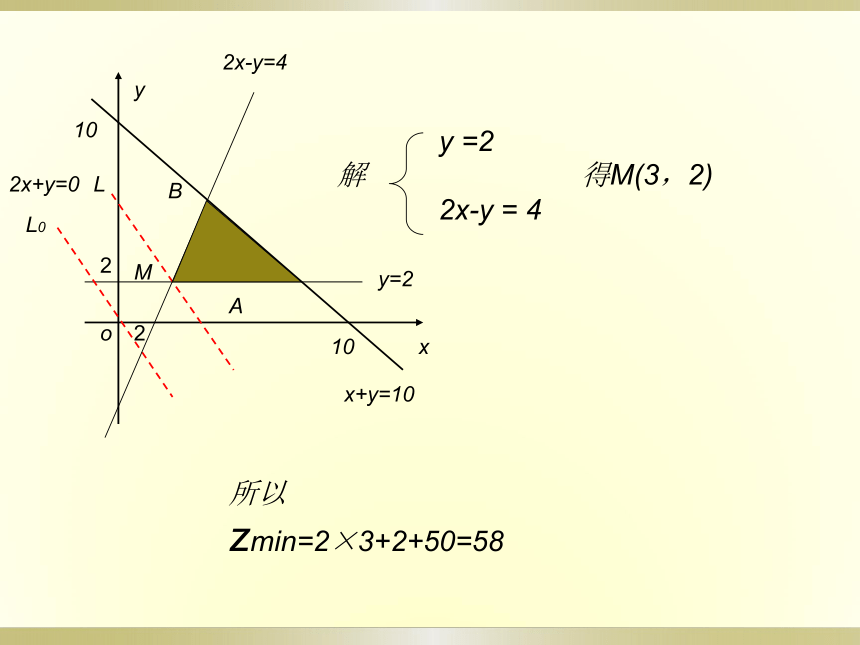
x ≥ 0平移2x+y=0可知点M为最优解y=2xy10L010oBAMx+y=102x+y=02x-y=422Ly =2
2x-y = 4
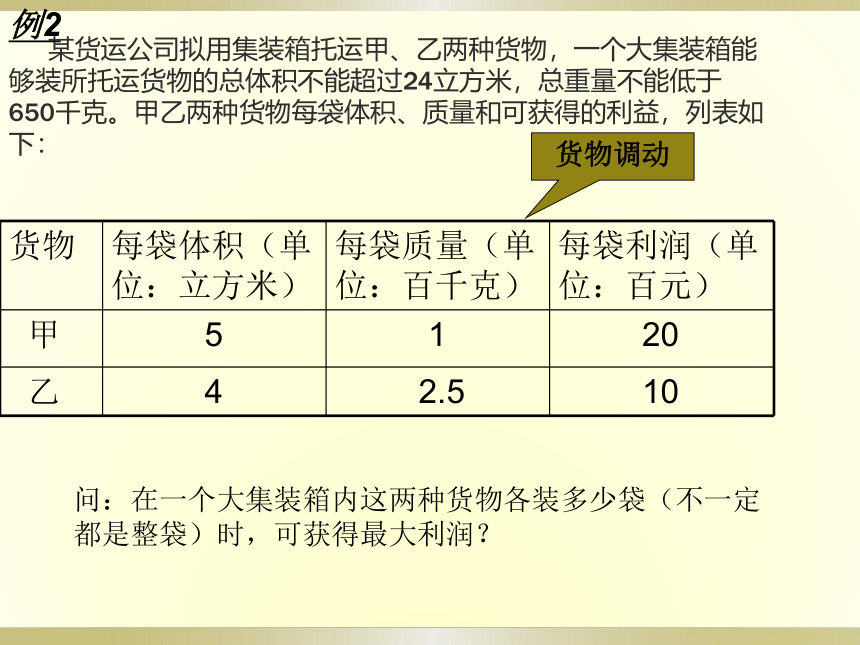
解得M(3,2)所以zmin=2×3+2+50=58 某货运公司拟用集装箱托运甲、乙两种货物,一个大集装箱能够装所托运货物的总体积不能超过24立方米,总重量不能低于650千克。甲乙两种货物每袋体积、质量和可获得的利益,列表如下: 例2问:在一个大集装箱内这两种货物各装多少袋(不一定都是整袋)时,可获得最大利润?货物调动解:设托运甲种货物x袋,乙种货物y袋,获得利润z百元,则依题意,则Z=20x+10y,且x,y满足条件5x+4y≤ 24
2x+5y≥ 13
x≥ 40 , y≥0 得点M(4,1).
因此当y等于x=4,y=1,z取得最大值,此时,
Zmax = 20×4+10×1=90
解2x+5y=135x+4y=24平移2x+y=0可知点M为最优解xy66oM5x+4y=2433L2x+5y=13L02x+y=0 A,B两个居民小区的居委会组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动,两个小区都有同学参加。已知A区的每位同学往返车费是3元,每人可为5位老人服务;B区的每位同学往返车费是3元,每人可为3位老人服务,如果要求B区参加的同学比A区同学多,且去敬老院的往返车费不超过37元。怎样安排A、B两区的同学,才能使受到服务的老人最多?受到服务的老人最多是多少?例3社区服务解:设A,B两区参与活动的人数分别为x , y ,
受到服务的老人的人数为z则 z=5x+3y,
y-x≥1
3x+5≤37
x≥1
x, y∈Nx-y=﹣1
3x+5y=37 得点M(4,5).
因此,当x=4,y=5时,z取得最大值,并且
Zmax=5×4+3×5=37.
解平移5x+3y=0知A为最优解xy77oAMx-y+1=015x+3y=0L0L. . .
. . . . .
. . . 本节待学习内容3.整点最优解得求解方法1.灵活多变的目标函数2.线性规划知识与其它知识的交汇若x,y满足x-y+2≥0x+y-4≥02x- y-5≤0① z = 的取值范围求例(一)灵活多变的目标函数②z = x2+y2-10y+25的最小值
Z=ax+by型
纵截距:3.Z=
(x,y)与(-d,-c)连线的斜率型型
∵ 1≤f(-1) ≤2,
2≤ f(1)≤4
例3 f(x)=ax2+bx,1≤f(-1) ≤2, 2≤ f(1)≤4,
求:f(-2)的取值范围。(二)线性规划与其它知识的交汇解:又f(-2)=4a-2b由线性规划知识可求得f(-2)的取值范围是(5,10)练习
等差数列﹛an﹜,-1≤a3≤1, 0≤a6≤3,求s9的取值范围。解:由题意可得1≤a1+2d≤1
0≤a1+5d≤3又S9=9a1+36d所以由线性规划知识可求得s9的取值范围是【-3,21】与其它知识的交汇转化思想线性规划模型方法1:(三)整点最优解得求解方法例1 某公司招收男职员x名,女职员y名,
x,y满足
求 z=10x+10y的最大值。5x-11y≥ -22
2x+3y≥ 9
2x≤ 11B ( 5,4 )方法2:例2 x,y满足不等式
2x-y-3≥ 0
2x+3y-6≤ 0
3x-5y-15≤ 0
求z=x-y(x,y为整数)的最大,最小值方法3:。。。。。x,y满足4x+3y-20≤20x-3y≤0x∈Ny∈N求S=7x+5y的最大值练习有一户房子室内面积共180平方米,想要拆分成两类房间作为旅游客房,大房间每间面积为18平方米,可住5名游客,每名游客每天住宿费40 元,小房间面积15平方米,每间可住游客3名,每名游客每天住宿费50元,装修大房间每间1000元,装修小房间每间用600元,如果只有8000元可以装修,且游客能住满房间,问应该拆分大小房间各多少间,才能获得最大利益?xyoM5x+3y=406x+5y=60课后思考题我还有新办法!小结:3.整点最优解得求解方法1.灵活多变的目标函数2.线性规划知识与其它知识的交汇oA(3,1)x+y-4=02x-y-5=0x-y+2=0再见
确定线性目标函数设:计划生产甲种产品x工时,生产乙种产品y时,则获得利润总额为z
则 z = 30x+40y
即 y=
其中x,y 满足 3x+2y≤1200
x+2y≤ 800
x≥ 0
y≥ 0
(3)确定线性约束条件
注意:把题目条件准确翻译为不等式组 解
3x+2y=1200
x+2y= 800
得 B(200,300)Zmax=30×200+40×300=18000L1:3x+2y-1200=0(4)画出可行域
①画线 ②定侧 ③求交(5)利用线性目标函数(直线)求出最优解平移3x+4y=0可知点B为最优解①变形 :由z=ax+by变为 y= -
求z的最值转化为求直线 y= 在y轴上的截距的最值。
(a,b是常数,z随x,y的变化而变化)
b>0时, 取最大值(或最小值)时z也取最大值(或
最小值);b< 0时, 取最大值,z取最小值。
取最小值时,z取最大值。
②平移:将ax+by=0平行移动,在可行域中,观察 截距 最大(或最小)时刚经过的点,即最优点
③求值:解有关方程组求出最优点的坐标,代入目标函数。求出目标函数的最值 下表给出甲乙丙三种食物中的维生素A、B的含量及单价营养师想购买这三种食物共10千克,使他们所含的维生素A不少于4400单位,维生素B不少于4800单位,而且要使付出的金额最低,这三种食物应各购买多少千克?例1食品配置解:设甲购买甲种食物x千克,乙种食物y千克,则购买丙种食物(10-x-y)千克。又设总支出为z元,依题意得 Z=7x+6y+5(10-x-y),
化简得z=2x+y+50.
x,y应满足的约束条件 400x+600y+400(10-x-y)≥ 4400
800x+200+400(10-x-y) ≥ 4800
x≥ 0 , y≥ 0
10-x-y≥ 0化简,得y ≥ 2
2x-y ≥ 4
X=y ≤ 10
x ≥ 0平移2x+y=0可知点M为最优解y=2xy10L010oBAMx+y=102x+y=02x-y=422Ly =2
2x-y = 4
解得M(3,2)所以zmin=2×3+2+50=58 某货运公司拟用集装箱托运甲、乙两种货物,一个大集装箱能够装所托运货物的总体积不能超过24立方米,总重量不能低于650千克。甲乙两种货物每袋体积、质量和可获得的利益,列表如下: 例2问:在一个大集装箱内这两种货物各装多少袋(不一定都是整袋)时,可获得最大利润?货物调动解:设托运甲种货物x袋,乙种货物y袋,获得利润z百元,则依题意,则Z=20x+10y,且x,y满足条件5x+4y≤ 24
2x+5y≥ 13
x≥ 40 , y≥0 得点M(4,1).
因此当y等于x=4,y=1,z取得最大值,此时,
Zmax = 20×4+10×1=90
解2x+5y=135x+4y=24平移2x+y=0可知点M为最优解xy66oM5x+4y=2433L2x+5y=13L02x+y=0 A,B两个居民小区的居委会组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动,两个小区都有同学参加。已知A区的每位同学往返车费是3元,每人可为5位老人服务;B区的每位同学往返车费是3元,每人可为3位老人服务,如果要求B区参加的同学比A区同学多,且去敬老院的往返车费不超过37元。怎样安排A、B两区的同学,才能使受到服务的老人最多?受到服务的老人最多是多少?例3社区服务解:设A,B两区参与活动的人数分别为x , y ,
受到服务的老人的人数为z则 z=5x+3y,
y-x≥1
3x+5≤37
x≥1
x, y∈Nx-y=﹣1
3x+5y=37 得点M(4,5).
因此,当x=4,y=5时,z取得最大值,并且
Zmax=5×4+3×5=37.
解平移5x+3y=0知A为最优解xy77oAMx-y+1=015x+3y=0L0L. . .
. . . . .
. . . 本节待学习内容3.整点最优解得求解方法1.灵活多变的目标函数2.线性规划知识与其它知识的交汇若x,y满足x-y+2≥0x+y-4≥02x- y-5≤0① z = 的取值范围求例(一)灵活多变的目标函数②z = x2+y2-10y+25的最小值
Z=ax+by型
纵截距:3.Z=
(x,y)与(-d,-c)连线的斜率型型
∵ 1≤f(-1) ≤2,
2≤ f(1)≤4
例3 f(x)=ax2+bx,1≤f(-1) ≤2, 2≤ f(1)≤4,
求:f(-2)的取值范围。(二)线性规划与其它知识的交汇解:又f(-2)=4a-2b由线性规划知识可求得f(-2)的取值范围是(5,10)练习
等差数列﹛an﹜,-1≤a3≤1, 0≤a6≤3,求s9的取值范围。解:由题意可得1≤a1+2d≤1
0≤a1+5d≤3又S9=9a1+36d所以由线性规划知识可求得s9的取值范围是【-3,21】与其它知识的交汇转化思想线性规划模型方法1:(三)整点最优解得求解方法例1 某公司招收男职员x名,女职员y名,
x,y满足
求 z=10x+10y的最大值。5x-11y≥ -22
2x+3y≥ 9
2x≤ 11B ( 5,4 )方法2:例2 x,y满足不等式
2x-y-3≥ 0
2x+3y-6≤ 0
3x-5y-15≤ 0
求z=x-y(x,y为整数)的最大,最小值方法3:。。。。。x,y满足4x+3y-20≤20x-3y≤0x∈Ny∈N求S=7x+5y的最大值练习有一户房子室内面积共180平方米,想要拆分成两类房间作为旅游客房,大房间每间面积为18平方米,可住5名游客,每名游客每天住宿费40 元,小房间面积15平方米,每间可住游客3名,每名游客每天住宿费50元,装修大房间每间1000元,装修小房间每间用600元,如果只有8000元可以装修,且游客能住满房间,问应该拆分大小房间各多少间,才能获得最大利益?xyoM5x+3y=406x+5y=60课后思考题我还有新办法!小结:3.整点最优解得求解方法1.灵活多变的目标函数2.线性规划知识与其它知识的交汇oA(3,1)x+y-4=02x-y-5=0x-y+2=0再见
