2.2.2 等差数列的前n项和 课件(21张PPT)
文档属性
| 名称 | 2.2.2 等差数列的前n项和 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 365.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 09:57:50 | ||
图片预览








文档简介
课件21张PPT。
第二章数列
2.2.2等差数列的前n项和
人教版数学B版必修5知识回顾
问题探索
概念形成
例题演示
课堂演练
课堂小结
课后作业
知识回顾1.等差数列的定义2.等差数列的通项公式
3.等差数列的性质,如果m+n=p+q,则an=a1+(n-1)d am+an =ap+aq
问题1:堆放着一堆钢管,第一层4根,下面每一层比上一层多放一根,共堆放 7层,这堆钢管共有多少根?
4,5,6,7,8,9,10你能快速求出这堆钢管共有多少根吗?下面再来看看:4+5+6+7+8+9+10的算法设S7=4+5+6+7+8+9+10 倒序S7=10+9+8+7+6+5+4多少个14 ?7个14 这个问题可以看成是求等差数列
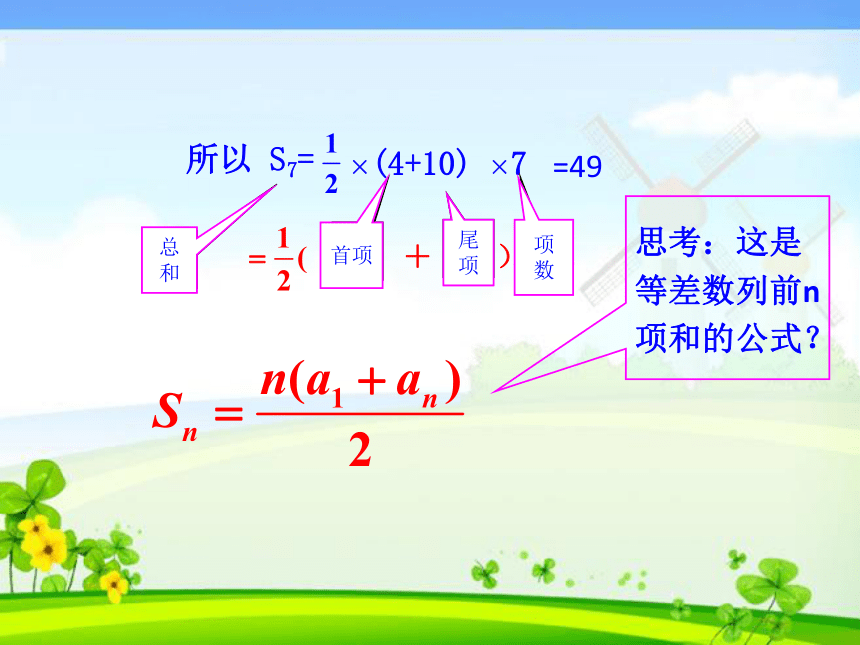
4,5,6,7,8,9,10的和所以 S7=×(4+10) ×7??首项尾项?总
和?项数思考:这是等差数列前n项和的公式?=49
①把项的次序反过来,Sn又可表示成:
②把①、②两边分别相加,得:设等差数列{an}前n项的和为Sn,由前面的问题的算法来探索下等差数列前n项和公式:概念形成由此得到等差数列 {an}的前n项和公式理解:
等差数列前n项的和等于首末项的和与项数乘积的一半上面的公式又可以写成 解题时需根据已知条件决定选用合适的公式例1:在等差数列{an}中, (1)a1=4,d=2,an=16,求Sn
(2)a3= -2,a8=12,求S10例题演示练习1:(1)2+4+6+8+ ······· 2n=?
( 2 ) 4+6+8+ ······· (2n-2)=?
例2 已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定其前n项和的公式吗? 想一想在等差数列 {an} 中,如果已知五个元素 a1, an, n, d, Sn 中的任意三个, 请问: 能否求出其余两个量 ?结论:知 三 求 二链接高考结论(2015课标全国Ⅱ卷)设Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5等于( )
A.5 B.7 C.9 D.11例3 等差数列{an}中,a1=25,S17=S9,求Sn的最大值?分析:本题可用二次函数求最值或由通项公式求n,使an≥0,an+1<0或利用等差数列的性质求出大于或等于零的项.解:方法一:由S17=S9,得方法二:先求出d=-2(同方法一)∵a1=25>0,∴当n=13时,Sn取得最大值169.
方法三:先求出d=-2(同方法一).
由S17=S9,得a10+a11+…+a17=0,
而a10+a17=a11+a16=a12+a15=a13+a14,
故a13+a14=0.
∵d=-2<0,a1>0,∴a13>0,a14<0.
故当n=13时,Sn取得最大值169.1.凸 n 边形各内角成等差数列,公差为 10o,最小内角为 100o,则n等于( )
(A)7 (B)8 (C)9 (D)8或 9由题意,得 :解得 n=8 或 9,但 n=9时, an=100 o+ (n-1) 10 o <180 o, n<9,a9=180 o,不合题意,故选(B)随堂演练2.等差数列{an}中, d=4, an=18, Sn=48,求a1的值?3.等差数列 -10,-6,-2,2,…前多少项的和是54? 解: 设题中的等差数列为{an},
则 a1= -10
d= -6-(-10)=4.
设 Sn= 54,得
???? 即 n2-6n-27=0
??????? 得 n1=9, n2=-3(舍去)。
?????? 因此等差数列 -10,-6,-2,2······· 前9项和是54。1.等差数列前n项和Sn公式的推导:
2.等差数列前n项和Sn公式的记忆与应用;说明:(1)正确合理的选择公式.
(2)注意与通项公式相结合.课堂小结倒序相加法课后作业1.教材P41-练习A1,2,3
练习B3,4
2.教材P40-思考讨论
第二章数列
2.2.2等差数列的前n项和
人教版数学B版必修5知识回顾
问题探索
概念形成
例题演示
课堂演练
课堂小结
课后作业
知识回顾1.等差数列的定义2.等差数列的通项公式
3.等差数列的性质,如果m+n=p+q,则an=a1+(n-1)d am+an =ap+aq
问题1:堆放着一堆钢管,第一层4根,下面每一层比上一层多放一根,共堆放 7层,这堆钢管共有多少根?
4,5,6,7,8,9,10你能快速求出这堆钢管共有多少根吗?下面再来看看:4+5+6+7+8+9+10的算法设S7=4+5+6+7+8+9+10 倒序S7=10+9+8+7+6+5+4多少个14 ?7个14 这个问题可以看成是求等差数列
4,5,6,7,8,9,10的和所以 S7=×(4+10) ×7??首项尾项?总
和?项数思考:这是等差数列前n项和的公式?=49
①把项的次序反过来,Sn又可表示成:
②把①、②两边分别相加,得:设等差数列{an}前n项的和为Sn,由前面的问题的算法来探索下等差数列前n项和公式:概念形成由此得到等差数列 {an}的前n项和公式理解:
等差数列前n项的和等于首末项的和与项数乘积的一半上面的公式又可以写成 解题时需根据已知条件决定选用合适的公式例1:在等差数列{an}中, (1)a1=4,d=2,an=16,求Sn
(2)a3= -2,a8=12,求S10例题演示练习1:(1)2+4+6+8+ ······· 2n=?
( 2 ) 4+6+8+ ······· (2n-2)=?
例2 已知一个等差数列的前10项的和是310,前20项的和是1220,由此可以确定其前n项和的公式吗? 想一想在等差数列 {an} 中,如果已知五个元素 a1, an, n, d, Sn 中的任意三个, 请问: 能否求出其余两个量 ?结论:知 三 求 二链接高考结论(2015课标全国Ⅱ卷)设Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5等于( )
A.5 B.7 C.9 D.11例3 等差数列{an}中,a1=25,S17=S9,求Sn的最大值?分析:本题可用二次函数求最值或由通项公式求n,使an≥0,an+1<0或利用等差数列的性质求出大于或等于零的项.解:方法一:由S17=S9,得方法二:先求出d=-2(同方法一)∵a1=25>0,∴当n=13时,Sn取得最大值169.
方法三:先求出d=-2(同方法一).
由S17=S9,得a10+a11+…+a17=0,
而a10+a17=a11+a16=a12+a15=a13+a14,
故a13+a14=0.
∵d=-2<0,a1>0,∴a13>0,a14<0.
故当n=13时,Sn取得最大值169.1.凸 n 边形各内角成等差数列,公差为 10o,最小内角为 100o,则n等于( )
(A)7 (B)8 (C)9 (D)8或 9由题意,得 :解得 n=8 或 9,但 n=9时, an=100 o+ (n-1) 10 o <180 o, n<9,a9=180 o,不合题意,故选(B)随堂演练2.等差数列{an}中, d=4, an=18, Sn=48,求a1的值?3.等差数列 -10,-6,-2,2,…前多少项的和是54? 解: 设题中的等差数列为{an},
则 a1= -10
d= -6-(-10)=4.
设 Sn= 54,得
???? 即 n2-6n-27=0
??????? 得 n1=9, n2=-3(舍去)。
?????? 因此等差数列 -10,-6,-2,2······· 前9项和是54。1.等差数列前n项和Sn公式的推导:
2.等差数列前n项和Sn公式的记忆与应用;说明:(1)正确合理的选择公式.
(2)注意与通项公式相结合.课堂小结倒序相加法课后作业1.教材P41-练习A1,2,3
练习B3,4
2.教材P40-思考讨论
