2.1.1 椭圆及其标准方程 课件(20张PPT)
文档属性
| 名称 | 2.1.1 椭圆及其标准方程 课件(20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 806.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 10:03:29 | ||
图片预览






文档简介
课件20张PPT。 北京时间2007年10月26日 05:31 中国首颗探月卫星“嫦娥一号”,在西昌卫星发射中心发射升空。
课题:椭圆及其标准方程(一) 画椭圆椭圆的定义:平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆小结:满足几个条件的动点的轨迹叫做椭圆?
[1]平面上----这是大前提
[2]动点 M 到两个定点 F1、F2 的距离之和
是常数 2a
[3]常数 2a 要大于焦距 2c两个定点叫做椭圆的焦点
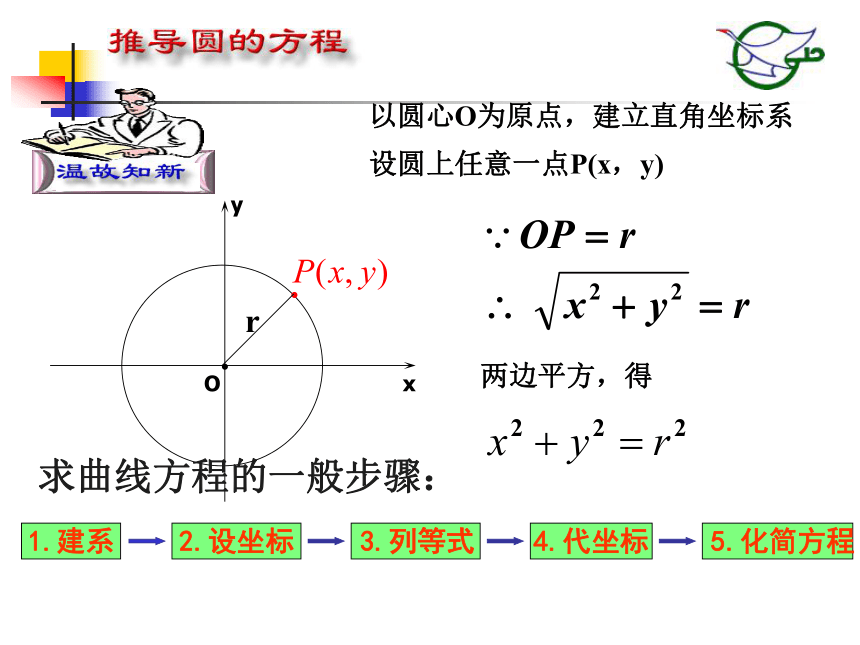
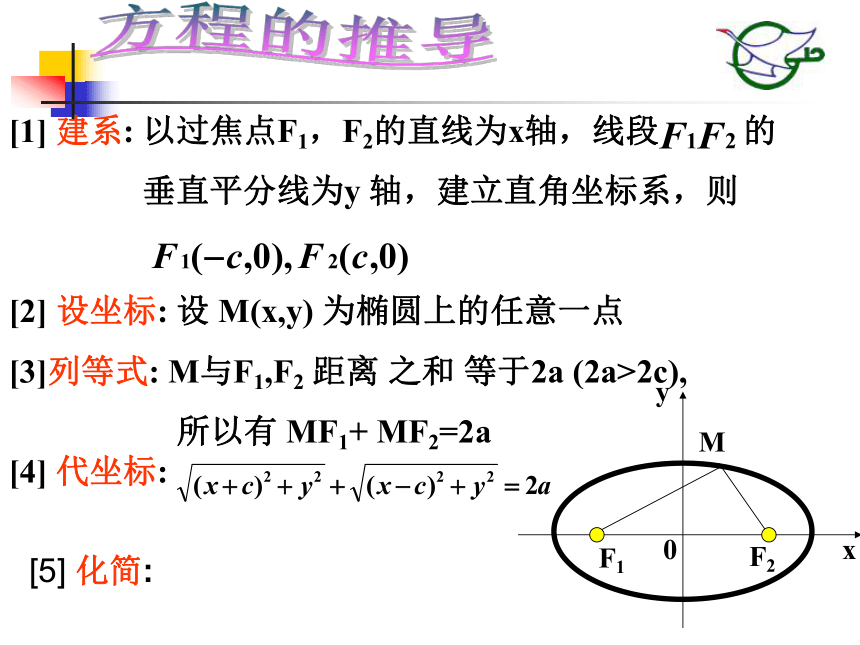
两焦点间的距离叫做椭圆的焦距2c思考:常数等于和小于|F1F2|分别表示什么图形? ——仙女座星系星系中的椭圆Or设圆上任意一点P(x,y) 以圆心O为原点,建立直角坐标系 两边平方,得 1.建系2.设坐标3.列等式4.代坐标求曲线方程的一般步骤: 5.化简方程[1] 建系: 以过焦点F1,F2的直线为x轴,线段 的
垂直平分线为y 轴,建立直角坐标系,则
[2] 设坐标: 设 M(x,y) 为椭圆上的任意一点
[3]列等式: M与F1,F2 距离 之和 等于2a (2a>2c),
所以有 MF1+ MF2=2a
[4] 代坐标:方程的推导[5] 化简:化标准三个数成等差数列的表示方法“x-d,x,x+d”
化标准联想图形返回椭圆的标准方程F1(0 ,-c)、F2(0, c)F1(-c,0)、F2(c,0)F1F2如何根据标准方程判断焦点在哪个坐标轴上? 两种形式的标准方程的比较:与(1)(2)在椭圆 中, a=___,b=___, 焦点位于____轴上,焦点坐标是__________. 32x在椭圆 中,a=___, b=___, 焦点位于____轴上,焦点坐标是__________. y4填空:、 .解:例2 :将圆 = 4上的点的横坐标保持不变,
纵坐标变为原来的一半,求所的曲线的方程,
并说明它是什么曲线?1)将圆按照某个方向均匀地压缩(拉长),可以得到椭圆。
2)利用中间变量求点的轨迹方程
的方法是解析几何中常用的方法;
分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹归纳、小结:a2=b2+c2
1.基础题:课本42页习题2.1 第2题、第4题
2.思考题:课后作业: 动圆与定圆
相内切且过定圆内的一个定点A(0,-2).
求动圆圆心P的轨迹方程.
课题:椭圆及其标准方程(一) 画椭圆椭圆的定义:平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆小结:满足几个条件的动点的轨迹叫做椭圆?
[1]平面上----这是大前提
[2]动点 M 到两个定点 F1、F2 的距离之和
是常数 2a
[3]常数 2a 要大于焦距 2c两个定点叫做椭圆的焦点
两焦点间的距离叫做椭圆的焦距2c思考:常数等于和小于|F1F2|分别表示什么图形? ——仙女座星系星系中的椭圆Or设圆上任意一点P(x,y) 以圆心O为原点,建立直角坐标系 两边平方,得 1.建系2.设坐标3.列等式4.代坐标求曲线方程的一般步骤: 5.化简方程[1] 建系: 以过焦点F1,F2的直线为x轴,线段 的
垂直平分线为y 轴,建立直角坐标系,则
[2] 设坐标: 设 M(x,y) 为椭圆上的任意一点
[3]列等式: M与F1,F2 距离 之和 等于2a (2a>2c),
所以有 MF1+ MF2=2a
[4] 代坐标:方程的推导[5] 化简:化标准三个数成等差数列的表示方法“x-d,x,x+d”
化标准联想图形返回椭圆的标准方程F1(0 ,-c)、F2(0, c)F1(-c,0)、F2(c,0)F1F2如何根据标准方程判断焦点在哪个坐标轴上? 两种形式的标准方程的比较:与(1)(2)在椭圆 中, a=___,b=___, 焦点位于____轴上,焦点坐标是__________. 32x在椭圆 中,a=___, b=___, 焦点位于____轴上,焦点坐标是__________. y4填空:、 .解:例2 :将圆 = 4上的点的横坐标保持不变,
纵坐标变为原来的一半,求所的曲线的方程,
并说明它是什么曲线?1)将圆按照某个方向均匀地压缩(拉长),可以得到椭圆。
2)利用中间变量求点的轨迹方程
的方法是解析几何中常用的方法;
分母哪个大,焦点就在哪个轴上平面内到两个定点F1,F2的距离的和等
于常数(大于F1F2)的点的轨迹归纳、小结:a2=b2+c2
1.基础题:课本42页习题2.1 第2题、第4题
2.思考题:课后作业: 动圆与定圆
相内切且过定圆内的一个定点A(0,-2).
求动圆圆心P的轨迹方程.
