2.1.1 椭圆及其标准方程 课件(24张PPT)
文档属性
| 名称 | 2.1.1 椭圆及其标准方程 课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 10:08:21 | ||
图片预览







文档简介
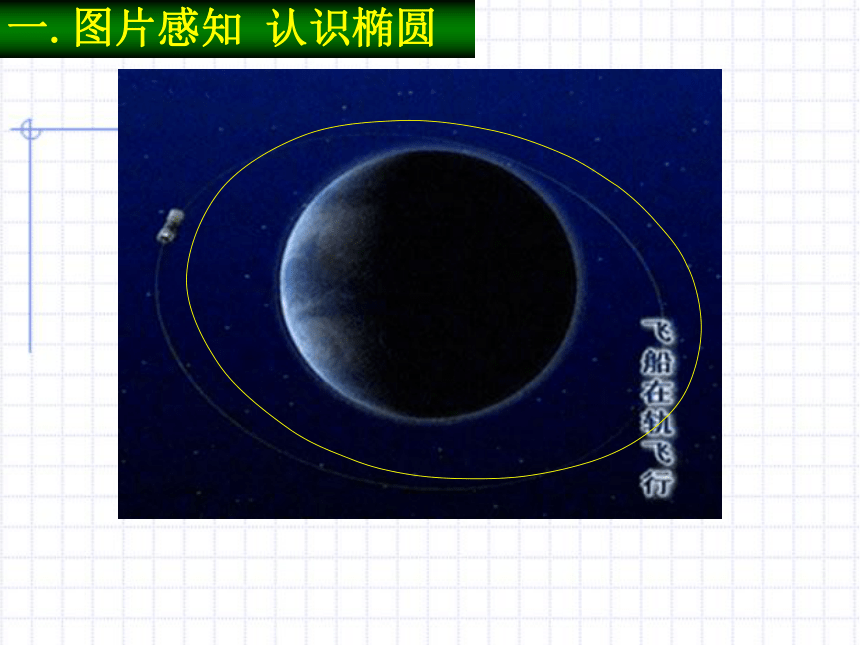
课件24张PPT。椭圆及其标准方程相 框一.图片感知 认识椭圆一.图片感知 认识椭圆国家大剧院一.图片感知 认识椭圆鸟巢被誉为“第四代体育馆”的伟大建筑作品一.图片感知 认识椭圆一.图片感知 认识椭圆实验一:
1、取一条一定长的细绳,把细绳的两端点合在一起用图钉固定在板上;
2、用铅笔尖(M)把细绳拉紧,在板上 慢慢移动,观察画出的图形是什么?
画圆
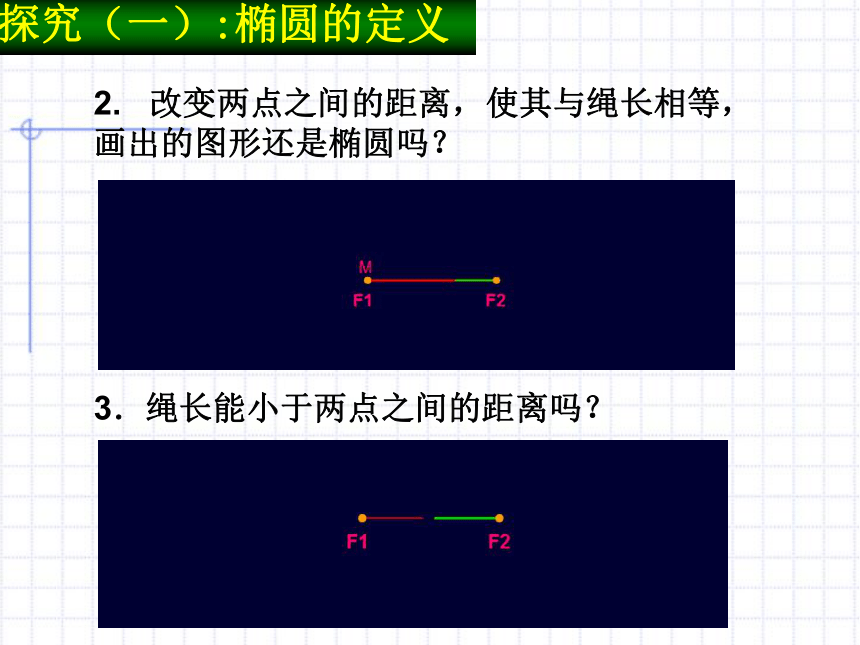
二.类比探究 形成概念请同学们小组合作,完成下列图形实验二:
(1)把细绳的两个端点分开,用图钉固定在板上的F1F2两点;
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看画出的图形。画椭圆二.类比探究 形成概念请同学们小组合作,完成下列图形2. 改变两点之间的距离,使其与绳长相等,画出的图形还是椭圆吗?3.绳长能小于两点之间的距离吗? 探究(一):椭圆的定义感悟: (3)若|MF1|+|MF2|<|F1F2|,动点M的轨迹(2)若|MF1|+|MF2|=|F1F2|,动点M的轨迹为探究(一):椭圆的定义椭圆线段F1F2不存在(1)若|MF1|+|MF2|>|F1F2|,动点M的轨迹为平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。这两个定点叫做椭圆的两焦点间的距离叫做椭圆的(2a>|F1F2|=2c)椭圆定义的
符号表述:椭圆定义的文字表述:探究(一):椭圆的定义焦点。焦距(一般用2c表示)。(1)必须在平面内;(2)两个定点---两点间距离确定(2c);(3)定长---轨迹上任意点到两定点距离和确定(2a).(4)|MF1|+|MF2|>|F1F2|(2a>2c>0)一点要注意哦1、定义中需要注意:探究(一):椭圆的定义建立平面直角坐标系通常遵循的原则:“对称”、“简洁”小组探讨建立平面直角坐标系的方案并求出椭圆的标准方程探究(二):椭圆的标准方程解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一点,椭
圆的焦距2c(c>0),M与F1和F2的距
离的和等于正常数2a (2a>2c) ,则
F1、F2的坐标分别 是(-c,0)、(c,0) .由椭圆的定义,椭圆就是集合:代入坐标(问题:下面怎样化简?)探究(二):椭圆的标准方程P={M||MF1|+|MF2|=2a}由椭圆定义可知两边再平方,得移项,再平方它表示:
① 椭圆的焦点在x轴
② 焦点坐标为F1(-c,0)、F2(c,0)
③ c2= a2 - b2 思考:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢探究(二):椭圆的标准方程探究(二):椭圆的标准方程它表示:① 椭圆的焦点在y轴
② 焦点坐标是F1(0,-c)、 F2(0,c)③ c2= a2 - b2 探究(二):椭圆的标准方程所谓椭圆的标准方程,一定是焦点在坐标轴上,且两焦点的中点为坐标原点。思考1:在图形中,a,b,c分别代表哪段的长度?探究(二):椭圆的标准方程思考2:在椭圆中a,b,c的大小关系(1)c2= a2 - b2
(2)a>b,a>c(3)b与c的大小关系不确定练习.用定义判断下列动点M的轨迹是否为椭圆。(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹。(2)到F1(-2,0)、F2(2,0)的距离之和为4的点的轨迹。(3)到F1(-2,0)、F2(2,0)的距离之和为3的点的轨迹。解 (1)因|MF1|+|MF2|=6>|F1F2|=4,故点M的轨迹为椭圆。(2)因|MF1|+|MF2|=4=|F1F2|=4,故点M的轨迹不是椭圆(是线段F1F2)。三.夯实基础 灵活运用(3)因|MF1|+|MF2|=3<|F1F2|=4,故点M的轨迹不存在答:在 X 轴。(-3,0)和(3,0)答:在 y 轴。(0,-5)和(0,5)例1:判定下列椭圆的标准方程在哪个轴上,并写出焦点坐标。 例题精析三.夯实基础 灵活运用请举手回答判断椭圆标准方程的焦点在哪条轴上的准则:
焦点在分母大的那个轴上。例2、填空:自由发言
已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则△F2CD的周长为________543(3,0)、(-3,0)620例3.椭圆的两个焦点的坐标分别是(-4,0),(4,0),
椭圆上一点M到两焦点距离之和等于10,求椭圆的标准方程。
迅速在练习本上写出过程,和答案对照讲评例题.
解: ∵椭圆的焦点在x轴上
∴设它的标准方程为:
∵ 2a=10, 2c=8
∴ a=5, c=4
∴ b2=a2-c2=52-42=9
∴所求椭圆的标准方程为
1、椭圆的定义(强调2a>|F1F2|=2c)和椭圆的标准方程 2、椭圆的标准方程有两种,注意区分 4、求椭圆标准方程的步骤 小结3、根据椭圆标准方程判断焦点位置的方法
1、取一条一定长的细绳,把细绳的两端点合在一起用图钉固定在板上;
2、用铅笔尖(M)把细绳拉紧,在板上 慢慢移动,观察画出的图形是什么?
画圆
二.类比探究 形成概念请同学们小组合作,完成下列图形实验二:
(1)把细绳的两个端点分开,用图钉固定在板上的F1F2两点;
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看画出的图形。画椭圆二.类比探究 形成概念请同学们小组合作,完成下列图形2. 改变两点之间的距离,使其与绳长相等,画出的图形还是椭圆吗?3.绳长能小于两点之间的距离吗? 探究(一):椭圆的定义感悟: (3)若|MF1|+|MF2|<|F1F2|,动点M的轨迹(2)若|MF1|+|MF2|=|F1F2|,动点M的轨迹为探究(一):椭圆的定义椭圆线段F1F2不存在(1)若|MF1|+|MF2|>|F1F2|,动点M的轨迹为平面内与两个定点F1、F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆。这两个定点叫做椭圆的两焦点间的距离叫做椭圆的(2a>|F1F2|=2c)椭圆定义的
符号表述:椭圆定义的文字表述:探究(一):椭圆的定义焦点。焦距(一般用2c表示)。(1)必须在平面内;(2)两个定点---两点间距离确定(2c);(3)定长---轨迹上任意点到两定点距离和确定(2a).(4)|MF1|+|MF2|>|F1F2|(2a>2c>0)一点要注意哦1、定义中需要注意:探究(一):椭圆的定义建立平面直角坐标系通常遵循的原则:“对称”、“简洁”小组探讨建立平面直角坐标系的方案并求出椭圆的标准方程探究(二):椭圆的标准方程解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一点,椭
圆的焦距2c(c>0),M与F1和F2的距
离的和等于正常数2a (2a>2c) ,则
F1、F2的坐标分别 是(-c,0)、(c,0) .由椭圆的定义,椭圆就是集合:代入坐标(问题:下面怎样化简?)探究(二):椭圆的标准方程P={M||MF1|+|MF2|=2a}由椭圆定义可知两边再平方,得移项,再平方它表示:
① 椭圆的焦点在x轴
② 焦点坐标为F1(-c,0)、F2(c,0)
③ c2= a2 - b2 思考:当椭圆的焦点在y轴上时,它的标准方程是怎样的呢探究(二):椭圆的标准方程探究(二):椭圆的标准方程它表示:① 椭圆的焦点在y轴
② 焦点坐标是F1(0,-c)、 F2(0,c)③ c2= a2 - b2 探究(二):椭圆的标准方程所谓椭圆的标准方程,一定是焦点在坐标轴上,且两焦点的中点为坐标原点。思考1:在图形中,a,b,c分别代表哪段的长度?探究(二):椭圆的标准方程思考2:在椭圆中a,b,c的大小关系(1)c2= a2 - b2
(2)a>b,a>c(3)b与c的大小关系不确定练习.用定义判断下列动点M的轨迹是否为椭圆。(1)到F1(-2,0)、F2(2,0)的距离之和为6的点的轨迹。(2)到F1(-2,0)、F2(2,0)的距离之和为4的点的轨迹。(3)到F1(-2,0)、F2(2,0)的距离之和为3的点的轨迹。解 (1)因|MF1|+|MF2|=6>|F1F2|=4,故点M的轨迹为椭圆。(2)因|MF1|+|MF2|=4=|F1F2|=4,故点M的轨迹不是椭圆(是线段F1F2)。三.夯实基础 灵活运用(3)因|MF1|+|MF2|=3<|F1F2|=4,故点M的轨迹不存在答:在 X 轴。(-3,0)和(3,0)答:在 y 轴。(0,-5)和(0,5)例1:判定下列椭圆的标准方程在哪个轴上,并写出焦点坐标。 例题精析三.夯实基础 灵活运用请举手回答判断椭圆标准方程的焦点在哪条轴上的准则:
焦点在分母大的那个轴上。例2、填空:自由发言
已知椭圆的方程为: ,则a=_____,b=_______,c=_______,焦点坐标为:____________焦距等于______;若CD为过左焦点F1的弦,则△F2CD的周长为________543(3,0)、(-3,0)620例3.椭圆的两个焦点的坐标分别是(-4,0),(4,0),
椭圆上一点M到两焦点距离之和等于10,求椭圆的标准方程。
迅速在练习本上写出过程,和答案对照讲评例题.
解: ∵椭圆的焦点在x轴上
∴设它的标准方程为:
∵ 2a=10, 2c=8
∴ a=5, c=4
∴ b2=a2-c2=52-42=9
∴所求椭圆的标准方程为
1、椭圆的定义(强调2a>|F1F2|=2c)和椭圆的标准方程 2、椭圆的标准方程有两种,注意区分 4、求椭圆标准方程的步骤 小结3、根据椭圆标准方程判断焦点位置的方法
