2.1.2 椭圆的几何性质 课件(19张PPT)
文档属性
| 名称 | 2.1.2 椭圆的几何性质 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 94.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 00:00:00 | ||
图片预览





文档简介
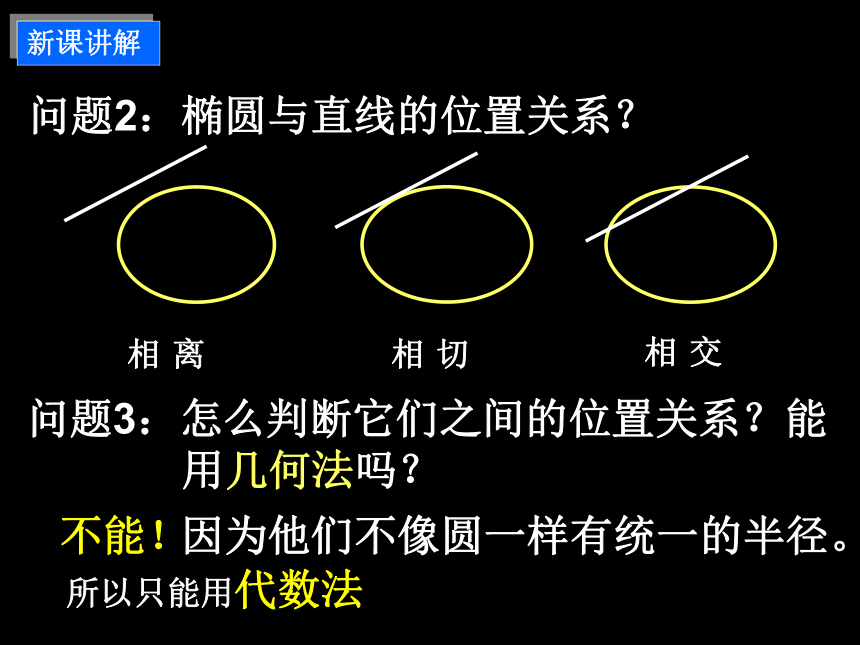
课件19张PPT。xy直线与椭圆的位置关系O点与椭圆的位置关系及判断1.点在椭圆外2.点在椭圆上3.点在椭圆内点P(x0,y0)与椭圆复习巩固 怎么判断它们之间的位置关系?问题1:直线与圆的位置关系有哪几种?d>r?>0?<0?=0几何法:代数法:复习巩固 dddd=rd 用几何法吗?问题2:椭圆与直线的位置关系?不能!所以只能用代数法因为他们不像圆一样有统一的半径。新课讲解 相 交相 切相 离例1:已知直线 与椭圆x2+4y2=2 ,
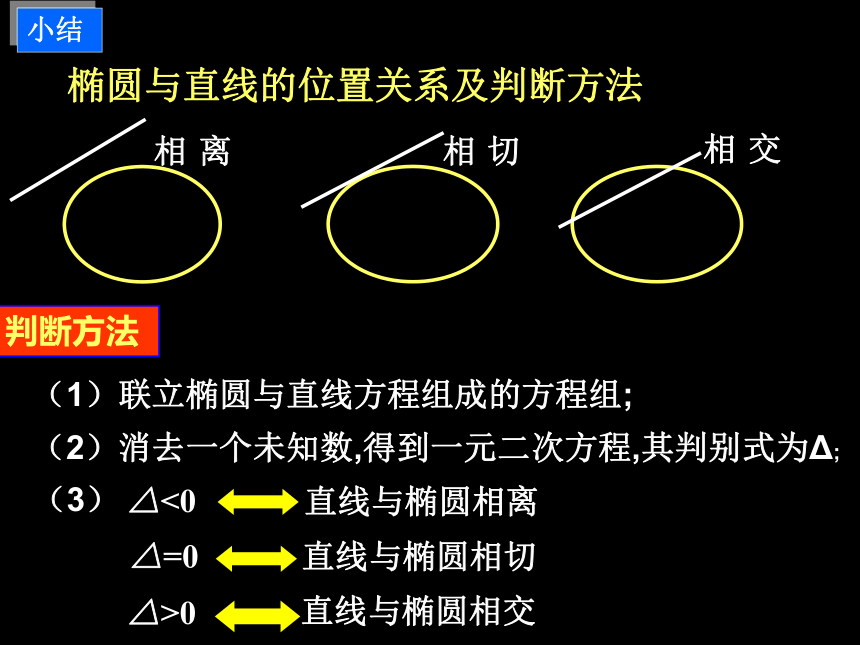
判断它们的位置关系。解:联立方程组消去y所以方程(1)有两个实数根,则原方程组有两组解, 即直线与椭圆相交。新课讲解(1) 椭圆与直线的位置关系及判断方法判断方法(1)联立椭圆与直线方程组成的方程组;(2)消去一个未知数,得到一元二次方程,其判别式为Δ;
(3)小结 相 交相 切相 离 k为何值时,直线y=kx+2和曲线2x2+3y2=6相交? 相切? 相离?小试牛刀 例2、 已知椭圆 和直线l:
4x-5y+40=0,试推断椭圆上是否存在一点,它到直线l的距离最小?最小距离是多少?方法一:切线法方法二:三角换元法mm例3:斜率为1的直线l过椭圆
的右焦点F2,交椭圆于A,B两点,求弦AB
之长.法1:解方程组得A、B的坐标再求|AB|法2:利用韦达定理与弦长公式求.设而不求1、直线与圆相交的弦长A(x1,y1)直线与二次曲线相交弦长的求法dr2、直线与其它二次曲线相交的弦长(1)联立方程组;(2)消去一个未知数;(3)利用弦长公式:|AB| =其中k 表示弦的斜率,x1、x2、y1、y2表示弦的
端点坐标,一般由韦达定理求得 x1+ x2 与 y1+ y2通法B(x2,y2) = 设而不求小结 方法1:求出A、B坐标,利用两点间距离公式;方法2:A(x1,y1)B(x2,y2)1、求椭圆 被过右焦点且垂
直于x轴的直线所截得的弦长。 小试牛刀 通 径相 交例题讲解 A(x2 , y2)M(x1 , y1)B例题讲解 解:依题意,所求直线斜率存在,设它的方程为y-1=k(x-2)把它代入椭圆方程并整理得:设直线与椭圆的交点为:A (x1 , y1)、B (x2 , y2)于是又M为AB的中点A(x2 , y2)Mxyo(x1 , y1)B故所求直线的方程为x+2y-4=0小结 弦中点、弦斜率问题的两种处理方法: (2)点差法:设弦的两端点坐标,代入
曲线方程相减后分解因式,便可与
弦所在直线的斜率及弦的中点联系
起来。 (1)联立方程组,消去一个未知数,利
用韦达定理解决; 变式 :已知椭圆 斜率为1
的直线l交椭圆于A,B,求弦AB的中点M的轨迹方程.小试牛刀 1、如果椭圆被 的弦被(4,2)平分,那
么这弦所在直线方程为( )
A、x-2y=0 B、x+2y- 4=0 C、2x+3y-12=0 D、x+2y-8=0
2、y=kx+1与椭圆 恰有公共点,则m的范围( )
A、(0,1) B、(0,5 )
C、[ 1,5)∪(5,+ ∞ ) D、(1,+ ∞ )
3、过椭圆 x2+2y2=4 的左焦点作倾斜角为300的直线,
则弦长 |AB|= _______ , 通径长是 _______ DC课堂练习 3、弦中点问题的两种处理方法:
(1)联立方程组,消去一个未知数,利用韦达定理;
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率。 1、直线与椭圆的三种位置关系及等价条件;2、弦长的计算方法:
(1)垂径定理:|AB|= (只适用于圆)
(2)弦长公式:
|AB|=
= (适用于任何二次曲线) 课堂小结 课后作业 1、已知直线2x-3y+6=0,焦点在y轴上
的椭圆x2+my2=m(m>0),在直线与椭圆
的关系如下时分别求m的取值范围: ⑴.相交;⑵.相切;⑶.相离.2、椭圆 与斜率为1的
直线l交于A,B两点,F1是左焦点,
求⊿ABF1的面积的最大值. 3、已知椭圆x2+4y2=16,过椭圆的右焦
点F2的直线l交椭圆于A,B,求弦
AB的中点M的轨迹方程.
判断它们的位置关系。解:联立方程组消去y所以方程(1)有两个实数根,则原方程组有两组解, 即直线与椭圆相交。新课讲解(1) 椭圆与直线的位置关系及判断方法判断方法(1)联立椭圆与直线方程组成的方程组;(2)消去一个未知数,得到一元二次方程,其判别式为Δ;
(3)小结 相 交相 切相 离 k为何值时,直线y=kx+2和曲线2x2+3y2=6相交? 相切? 相离?小试牛刀 例2、 已知椭圆 和直线l:
4x-5y+40=0,试推断椭圆上是否存在一点,它到直线l的距离最小?最小距离是多少?方法一:切线法方法二:三角换元法mm例3:斜率为1的直线l过椭圆
的右焦点F2,交椭圆于A,B两点,求弦AB
之长.法1:解方程组得A、B的坐标再求|AB|法2:利用韦达定理与弦长公式求.设而不求1、直线与圆相交的弦长A(x1,y1)直线与二次曲线相交弦长的求法dr2、直线与其它二次曲线相交的弦长(1)联立方程组;(2)消去一个未知数;(3)利用弦长公式:|AB| =其中k 表示弦的斜率,x1、x2、y1、y2表示弦的
端点坐标,一般由韦达定理求得 x1+ x2 与 y1+ y2通法B(x2,y2) = 设而不求小结 方法1:求出A、B坐标,利用两点间距离公式;方法2:A(x1,y1)B(x2,y2)1、求椭圆 被过右焦点且垂
直于x轴的直线所截得的弦长。 小试牛刀 通 径相 交例题讲解 A(x2 , y2)M(x1 , y1)B例题讲解 解:依题意,所求直线斜率存在,设它的方程为y-1=k(x-2)把它代入椭圆方程并整理得:设直线与椭圆的交点为:A (x1 , y1)、B (x2 , y2)于是又M为AB的中点A(x2 , y2)Mxyo(x1 , y1)B故所求直线的方程为x+2y-4=0小结 弦中点、弦斜率问题的两种处理方法: (2)点差法:设弦的两端点坐标,代入
曲线方程相减后分解因式,便可与
弦所在直线的斜率及弦的中点联系
起来。 (1)联立方程组,消去一个未知数,利
用韦达定理解决; 变式 :已知椭圆 斜率为1
的直线l交椭圆于A,B,求弦AB的中点M的轨迹方程.小试牛刀 1、如果椭圆被 的弦被(4,2)平分,那
么这弦所在直线方程为( )
A、x-2y=0 B、x+2y- 4=0 C、2x+3y-12=0 D、x+2y-8=0
2、y=kx+1与椭圆 恰有公共点,则m的范围( )
A、(0,1) B、(0,5 )
C、[ 1,5)∪(5,+ ∞ ) D、(1,+ ∞ )
3、过椭圆 x2+2y2=4 的左焦点作倾斜角为300的直线,
则弦长 |AB|= _______ , 通径长是 _______ DC课堂练习 3、弦中点问题的两种处理方法:
(1)联立方程组,消去一个未知数,利用韦达定理;
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率。 1、直线与椭圆的三种位置关系及等价条件;2、弦长的计算方法:
(1)垂径定理:|AB|= (只适用于圆)
(2)弦长公式:
|AB|=
= (适用于任何二次曲线) 课堂小结 课后作业 1、已知直线2x-3y+6=0,焦点在y轴上
的椭圆x2+my2=m(m>0),在直线与椭圆
的关系如下时分别求m的取值范围: ⑴.相交;⑵.相切;⑶.相离.2、椭圆 与斜率为1的
直线l交于A,B两点,F1是左焦点,
求⊿ABF1的面积的最大值. 3、已知椭圆x2+4y2=16,过椭圆的右焦
点F2的直线l交椭圆于A,B,求弦
AB的中点M的轨迹方程.
