2.2.2 双曲线的几何性质课件(24张PPT)
文档属性
| 名称 | 2.2.2 双曲线的几何性质课件(24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 00:00:00 | ||
图片预览







文档简介
课件24张PPT。2.3.1抛物线及其标准方程抛物线及其标准方程生活中的抛物线美丽的赵州桥生活中的抛物线北京2008奥林匹克体育馆生活中的抛物线上海卢浦大桥抛球运动展示课前实践作业小实验:
准备一张作业纸,竖直放置,在纸的下边靠上大约3厘米且左右居中的位置画上一点F。把纸的下边缘上的某点(比如B)翻折与点F重合。把纸压平,得到一条折痕。取不同的点B,可以得到一系列的折痕。取遍底边上的所有点,就得到一系列连续变化的折痕,那么,与所有这些折痕都相切的曲线是什么?
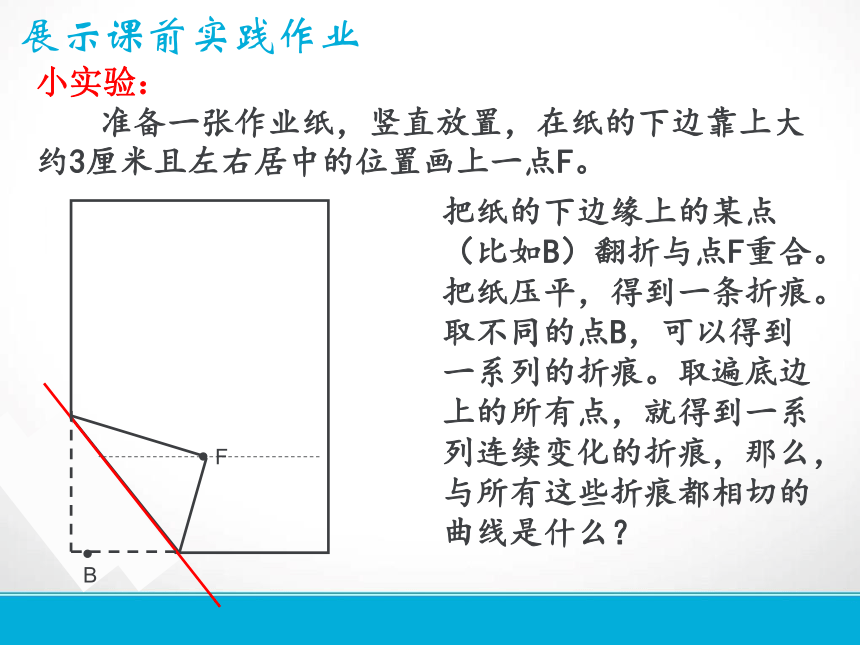
展示课前实践作业小实验:
准备一张作业纸,竖直放置,在纸的下边靠上大约3厘米且左右居中的位置画上一点F。把纸的下边缘上的某点(比如B)翻折与点F重合。把纸压平,得到一条折痕。取不同的点B,可以得到一系列的折痕。取遍底边上的所有点,就得到一系列连续变化的折痕,那么,与所有这些折痕都相切的曲线是什么?
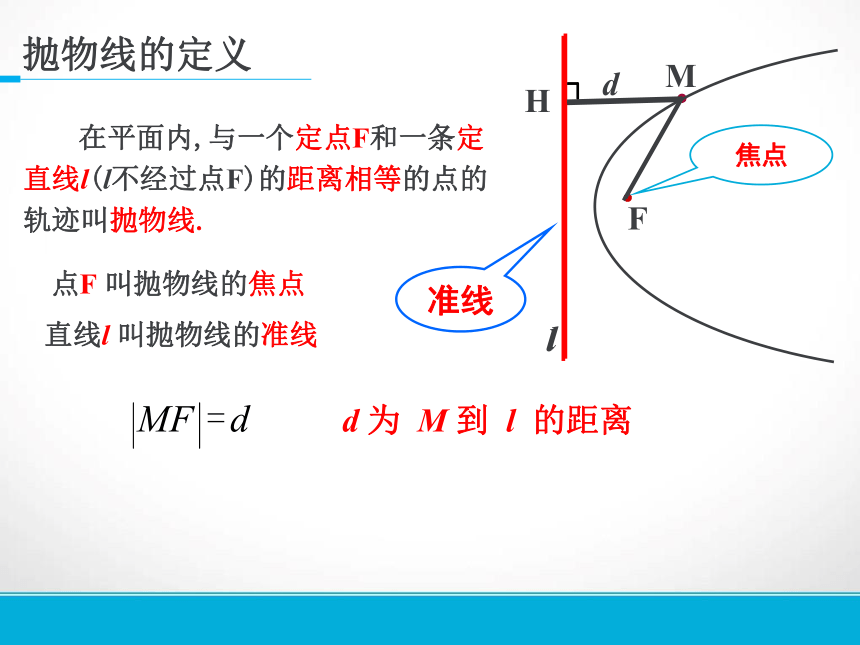
抛物线的定义 在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F 叫抛物线的焦点d 为 M 到 l 的距离准线dHl直线l 叫抛物线的准线
焦点展示课前实践作业小实验:
准备一张作业纸,竖直放置,在纸的下边靠上大约3厘米且左右居中的位置画上一点F。把纸的下边缘上的某点(比如B)翻折与点F重合。把纸压平,得到一条折痕。取不同的点B,可以得到一系列的折痕。取遍底边上的所有点,就得到一系列连续变化的折痕,那么,与所有这些折痕都相切的曲线是什么?
直角三角板方法 在点F与纸下底边之间画一条平行于底边的直线a,让它到点F和到底边的距离相等,取来一块直角三角板,让直角项点A位于直线a上。让一条直角边过点F。然后,沿另一条直角边画线b。改变A在a上的位置,做同样的事情。那么,直线b的轨迹就会包含一个抛物线。抛物线的定义 在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F 叫抛物线的焦点d 为 M 到 l 的距离准线dHl直线l 叫抛物线的准线
焦点思考1:1. 若l经过点F,动点M的轨迹是什么?2.比较椭圆、双曲线标准方程的建立过程,你认为如 何选择坐标系,建立的抛物线的方程才能更简单?课堂探究.xyKFl.xyKFl.xyKFlO如何求写抛物线方程呢?
课堂探究思考2:.建系一:
以KF所在直线为x轴,以K为原点建立直角坐标系,则F(p,0)设动点M(x,y),
由定义得动点M限制条件:化简得:d将M(x,y)代入得:不同建系下的方程比较抛物线的标准方程y2 = 2px(p>0)其中p 为正常数,它的几何意义是: 焦 点 到 准 线 的 距 离方程 y2 = 2px(p>0)
表示焦点在x轴正半轴上的抛物线.抛物线的标准方程如何确定抛物线焦点位置及开口方向?图形标准方程焦点坐标准线方程巩固加深1、求抛物线的焦点或准线时,
一定要先把方程化为标准方程;2、不确定开口方向,
一定要分情况讨论。课堂小结 抛物线的标准方程y2=2px (p>0)p: 焦点到准线的距离.顶点: 原点 (0, 0)焦点:准线:课后作业1.作业十七:
必做题1-7 选做题8-122.自主预习下节内容 圆锥曲线统一定义的背景和应用 3.兴趣阅读:谢谢大家!探照灯、汽车前灯的反光曲面,手电筒的反光镜面、太阳灶的镜面都是抛物镜面。抛物镜面:抛物线绕其对称轴旋转而成的曲面。灯泡放在抛物线的焦点位置上,通过镜面反射就变
成了平行光束,这就是探照灯、汽车前灯、手电筒的
设计原理。平行光线射到抛物镜面上,经镜面反射后,反射光线都
经过抛物线的焦点,这就是太阳灶能把光能转化为热能
的理论依据。例2:探照灯反射镜的轴截面是抛物线的一部分,光源
位于抛物线的焦点处。已知灯口圆的直径为60cm,灯深
40cm,求抛物线的标准方程和焦点位置。x(40,30)解:设抛物线的标准方程为:y2=2px由条件可得A (40,30),代入方程得:302=2p·40解之: p=故所求抛物线的标准方程为: y2= x,焦点为( ,0)
准备一张作业纸,竖直放置,在纸的下边靠上大约3厘米且左右居中的位置画上一点F。把纸的下边缘上的某点(比如B)翻折与点F重合。把纸压平,得到一条折痕。取不同的点B,可以得到一系列的折痕。取遍底边上的所有点,就得到一系列连续变化的折痕,那么,与所有这些折痕都相切的曲线是什么?
展示课前实践作业小实验:
准备一张作业纸,竖直放置,在纸的下边靠上大约3厘米且左右居中的位置画上一点F。把纸的下边缘上的某点(比如B)翻折与点F重合。把纸压平,得到一条折痕。取不同的点B,可以得到一系列的折痕。取遍底边上的所有点,就得到一系列连续变化的折痕,那么,与所有这些折痕都相切的曲线是什么?
抛物线的定义 在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F 叫抛物线的焦点d 为 M 到 l 的距离准线dHl直线l 叫抛物线的准线
焦点展示课前实践作业小实验:
准备一张作业纸,竖直放置,在纸的下边靠上大约3厘米且左右居中的位置画上一点F。把纸的下边缘上的某点(比如B)翻折与点F重合。把纸压平,得到一条折痕。取不同的点B,可以得到一系列的折痕。取遍底边上的所有点,就得到一系列连续变化的折痕,那么,与所有这些折痕都相切的曲线是什么?
直角三角板方法 在点F与纸下底边之间画一条平行于底边的直线a,让它到点F和到底边的距离相等,取来一块直角三角板,让直角项点A位于直线a上。让一条直角边过点F。然后,沿另一条直角边画线b。改变A在a上的位置,做同样的事情。那么,直线b的轨迹就会包含一个抛物线。抛物线的定义 在平面内,与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫抛物线.点F 叫抛物线的焦点d 为 M 到 l 的距离准线dHl直线l 叫抛物线的准线
焦点思考1:1. 若l经过点F,动点M的轨迹是什么?2.比较椭圆、双曲线标准方程的建立过程,你认为如 何选择坐标系,建立的抛物线的方程才能更简单?课堂探究.xyKFl.xyKFl.xyKFlO如何求写抛物线方程呢?
课堂探究思考2:.建系一:
以KF所在直线为x轴,以K为原点建立直角坐标系,则F(p,0)设动点M(x,y),
由定义得动点M限制条件:化简得:d将M(x,y)代入得:不同建系下的方程比较抛物线的标准方程y2 = 2px(p>0)其中p 为正常数,它的几何意义是: 焦 点 到 准 线 的 距 离方程 y2 = 2px(p>0)
表示焦点在x轴正半轴上的抛物线.抛物线的标准方程如何确定抛物线焦点位置及开口方向?图形标准方程焦点坐标准线方程巩固加深1、求抛物线的焦点或准线时,
一定要先把方程化为标准方程;2、不确定开口方向,
一定要分情况讨论。课堂小结 抛物线的标准方程y2=2px (p>0)p: 焦点到准线的距离.顶点: 原点 (0, 0)焦点:准线:课后作业1.作业十七:
必做题1-7 选做题8-122.自主预习下节内容 圆锥曲线统一定义的背景和应用 3.兴趣阅读:谢谢大家!探照灯、汽车前灯的反光曲面,手电筒的反光镜面、太阳灶的镜面都是抛物镜面。抛物镜面:抛物线绕其对称轴旋转而成的曲面。灯泡放在抛物线的焦点位置上,通过镜面反射就变
成了平行光束,这就是探照灯、汽车前灯、手电筒的
设计原理。平行光线射到抛物镜面上,经镜面反射后,反射光线都
经过抛物线的焦点,这就是太阳灶能把光能转化为热能
的理论依据。例2:探照灯反射镜的轴截面是抛物线的一部分,光源
位于抛物线的焦点处。已知灯口圆的直径为60cm,灯深
40cm,求抛物线的标准方程和焦点位置。x(40,30)解:设抛物线的标准方程为:y2=2px由条件可得A (40,30),代入方程得:302=2p·40解之: p=故所求抛物线的标准方程为: y2= x,焦点为( ,0)
