1.3.2 命题的四种形式 课件(19张PPT)
文档属性
| 名称 | 1.3.2 命题的四种形式 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 128.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 00:00:00 | ||
图片预览





文档简介
课件19张PPT。1.3.2
四种命题教学目标
1.了解命题的逆命题、否命题与逆否命题;会分析四种命题之间的相互关系;
2.会利用互为逆否命题的两个命题之间的关系判别命题的真假.
重点
四种命题的相互关系.
难点
由原命题准确写出另外三种命题,判断真假。
若一个整数的末位是0,则它可以被5整除。若一条直线到圆心的距离不等于半径,则它不是圆的切线。练习 把下列命题改写成“若P则q”的形式 (1)末位是0的整数,可以被5整除; (2)到圆心的距离不等于半径的直线不是圆的切线;回顾:“若p,则q”的形式命题,通常把这种命题中的p叫做命题的条件,q叫做结论(1)如果两个三角形全等,那么它们的面积相等.
(2)如果两个三角形的面积相等,那么它们全等.
(3)如果两个三角形不全等,那么它们的面积不相等.
(4)如果两个三角形的面积不相等,那么它们不全等.
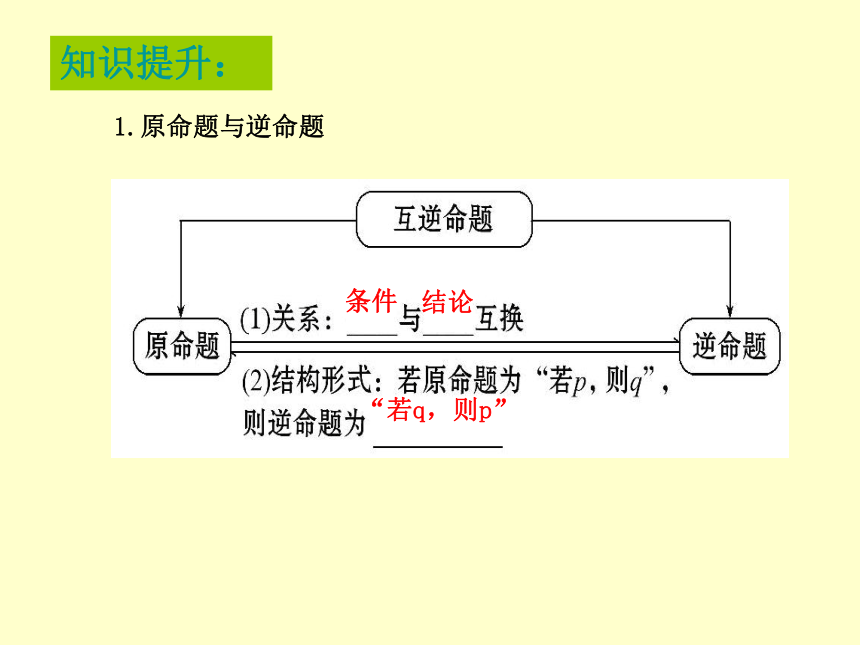
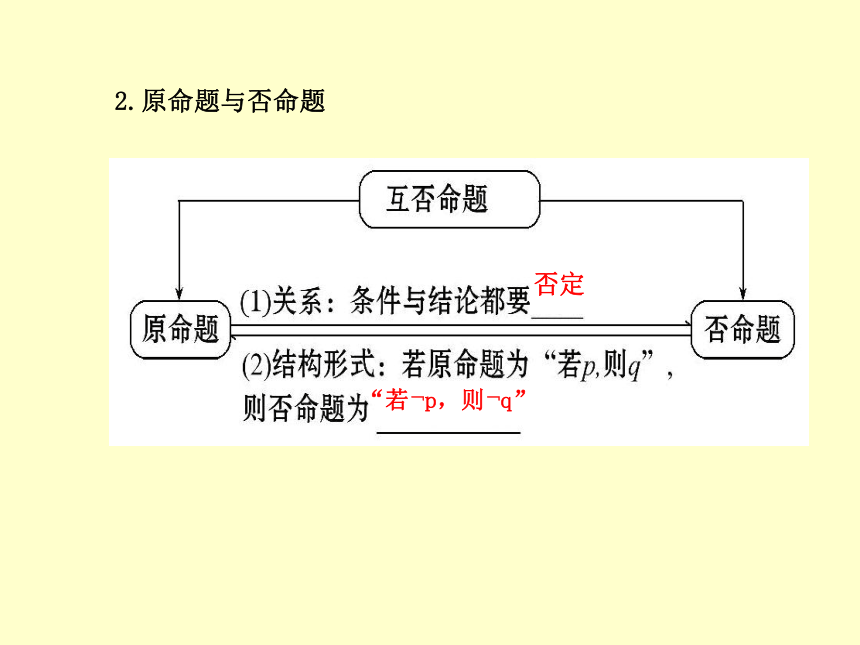
如果第一个命题的条件和结论是第二个命题的条件和结论的否定,那么这两个命题叫做互否命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的否命题。 如果第一个命题的条件和结论分别是第二个命题的结论的否定和条件的否定,那么这两个命题叫做互为逆否命题。如果把其中一个命题叫做原命题那么另一个叫做原命题的逆否命题 如果第一个命题的条件(或题设)是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫互逆命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的逆命题。授新:四种命题定义1、互逆命题:2、互否命题: 3、互为逆否命题:1.原命题与逆命题条件结论“若q,则p”知识提升:2.原命题与否命题否定“若﹁p,则﹁q”3.原命题与逆否命题“若﹁q,则﹁p”否定互换如果p,则q如果q,则p互逆如果非p,则非q如果非q,则非p互否互否互逆例题:分别写出下列各命题的逆命题、否命题和逆否命题:并判断真假 (1)正方形的四边相等。 逆命题:如果一个四边形四边相等,那么它是正方形。否命题:如果一个四边形不是正方形,那么它的四条边不相等。逆否命题:如果一个四边形四边不相等,那么它不是正方形。原命题: 如果一个四边形是正方形,那么它的四条边相等。 (2)若X=1或X=2,
则X2-3X+2=0。 逆命题:
若X2-3X+2=0, 则X=1或X=2 。否命题:
若X?1且X?2,
则X2-3X+2 ?0。逆否命题:
若X2-3X+2 ? 0,
则X?1且X? 2 。1:要写出一个命题的另外三个命题关键是分清命题的题设和结论(即把原命题写成“若P则q”的形式)2:(1)“或”的否定为“且”,
(2)“且”的否定为“或”,
(3)“都”的否定为“不都”。提升结论:1.判一判(正确的打“√”,错误的打“×”)
(1)有的命题没有逆命题.( )
(2)“对顶角相等”的否命题为“对顶角不相等”.( )
(3)原命题的否命题的逆命题就是原命题的逆否命题.( )巩固练习【解析】(1)错误.任何命题都是由条件和结论构成的,所以任何命题都有逆命题.
(2)错误.“对顶角相等”的否命题为“不是对顶角的两个角不相等”.
(3)正确.原命题“若p,则q”的否命题为“若﹁p,则﹁q”,这个命题的逆命题为“若﹁q,则﹁p”,这就是原命题的逆否命题.
答案:(1)× (2)× (3)√2.做一做(请把正确的答案写在横线上)
(1)若a=0,则ab=0的逆命题是 .
(2)若命题r的否命题为“若﹁p,则q”,那么原命题r为________.
(3)若a=b,则|a|=|b|的逆否命题是 .【解析】(1)逆命题只需把原命题的条件与结论互换即可,即逆命题为若ab=0,则a=0.
答案:若ab=0,则a=0
(2)因为原命题与否命题为互否命题,所以只需求“若﹁p,则q”的否命题即可,其否命题为“若p,则﹁q”.
答案:“若p,则﹁q”
(3)逆否命题既需要把原命题的条件与结论否定,又需要互换,故已知命题的逆否命题是:若|a|≠|b|,则a≠b.
答案:若|a|≠|b|,则a≠b3、填空:
(1)命题“末位于0的整数,可以被5整除”的逆命题是:(2)命题“线段的垂直平分线上的点与这 条线段两端点的距离相等”的否命题是: (3)命题“对顶角相等”的逆否命题是:若一个整数可以被5整除,则它的末位是0。 若一个点不在线段的垂直平分线上,则它到这条线段两端点的距离不相等。若两个角不相等,则它们不是对顶角。4.写出下列各命题的逆命题,否命题,逆否命题,并判断其真假
(1)如果x≧5,那么x≧2
(2)如果一个函数是偶函数,则它的图像关于y轴成轴对称图形。
提升原命题的真假和它的否命题,逆命题,逆否命
题之间的真假分别有什么关系?原命题与它的逆命题,原命题和它的否命题之间的真假是不定的,而原命题和它的逆否命题之间在真假上始终保持一致的:同真或同假。
即:互为逆否的两个命题等价
互逆或互否的两个命题不等价小结:
四种命题的转换方法
(1)交换原命题的条件和结论,所得命题是原命题的逆命题.
(2)同时否定原命题的条件和结论,所得命题是原命题的否命题.
(3)交换原命题的条件和结论,并且同时否定,所得命题是原命题的逆否命题.
根据学习本节的知识提高自己的解决问题的能力。
作业:
习题1-3A 2、3、5
四种命题教学目标
1.了解命题的逆命题、否命题与逆否命题;会分析四种命题之间的相互关系;
2.会利用互为逆否命题的两个命题之间的关系判别命题的真假.
重点
四种命题的相互关系.
难点
由原命题准确写出另外三种命题,判断真假。
若一个整数的末位是0,则它可以被5整除。若一条直线到圆心的距离不等于半径,则它不是圆的切线。练习 把下列命题改写成“若P则q”的形式 (1)末位是0的整数,可以被5整除; (2)到圆心的距离不等于半径的直线不是圆的切线;回顾:“若p,则q”的形式命题,通常把这种命题中的p叫做命题的条件,q叫做结论(1)如果两个三角形全等,那么它们的面积相等.
(2)如果两个三角形的面积相等,那么它们全等.
(3)如果两个三角形不全等,那么它们的面积不相等.
(4)如果两个三角形的面积不相等,那么它们不全等.
如果第一个命题的条件和结论是第二个命题的条件和结论的否定,那么这两个命题叫做互否命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的否命题。 如果第一个命题的条件和结论分别是第二个命题的结论的否定和条件的否定,那么这两个命题叫做互为逆否命题。如果把其中一个命题叫做原命题那么另一个叫做原命题的逆否命题 如果第一个命题的条件(或题设)是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫互逆命题。如果把其中一个命题叫做原命题,那么另一个叫做原命题的逆命题。授新:四种命题定义1、互逆命题:2、互否命题: 3、互为逆否命题:1.原命题与逆命题条件结论“若q,则p”知识提升:2.原命题与否命题否定“若﹁p,则﹁q”3.原命题与逆否命题“若﹁q,则﹁p”否定互换如果p,则q如果q,则p互逆如果非p,则非q如果非q,则非p互否互否互逆例题:分别写出下列各命题的逆命题、否命题和逆否命题:并判断真假 (1)正方形的四边相等。 逆命题:如果一个四边形四边相等,那么它是正方形。否命题:如果一个四边形不是正方形,那么它的四条边不相等。逆否命题:如果一个四边形四边不相等,那么它不是正方形。原命题: 如果一个四边形是正方形,那么它的四条边相等。 (2)若X=1或X=2,
则X2-3X+2=0。 逆命题:
若X2-3X+2=0, 则X=1或X=2 。否命题:
若X?1且X?2,
则X2-3X+2 ?0。逆否命题:
若X2-3X+2 ? 0,
则X?1且X? 2 。1:要写出一个命题的另外三个命题关键是分清命题的题设和结论(即把原命题写成“若P则q”的形式)2:(1)“或”的否定为“且”,
(2)“且”的否定为“或”,
(3)“都”的否定为“不都”。提升结论:1.判一判(正确的打“√”,错误的打“×”)
(1)有的命题没有逆命题.( )
(2)“对顶角相等”的否命题为“对顶角不相等”.( )
(3)原命题的否命题的逆命题就是原命题的逆否命题.( )巩固练习【解析】(1)错误.任何命题都是由条件和结论构成的,所以任何命题都有逆命题.
(2)错误.“对顶角相等”的否命题为“不是对顶角的两个角不相等”.
(3)正确.原命题“若p,则q”的否命题为“若﹁p,则﹁q”,这个命题的逆命题为“若﹁q,则﹁p”,这就是原命题的逆否命题.
答案:(1)× (2)× (3)√2.做一做(请把正确的答案写在横线上)
(1)若a=0,则ab=0的逆命题是 .
(2)若命题r的否命题为“若﹁p,则q”,那么原命题r为________.
(3)若a=b,则|a|=|b|的逆否命题是 .【解析】(1)逆命题只需把原命题的条件与结论互换即可,即逆命题为若ab=0,则a=0.
答案:若ab=0,则a=0
(2)因为原命题与否命题为互否命题,所以只需求“若﹁p,则q”的否命题即可,其否命题为“若p,则﹁q”.
答案:“若p,则﹁q”
(3)逆否命题既需要把原命题的条件与结论否定,又需要互换,故已知命题的逆否命题是:若|a|≠|b|,则a≠b.
答案:若|a|≠|b|,则a≠b3、填空:
(1)命题“末位于0的整数,可以被5整除”的逆命题是:(2)命题“线段的垂直平分线上的点与这 条线段两端点的距离相等”的否命题是: (3)命题“对顶角相等”的逆否命题是:若一个整数可以被5整除,则它的末位是0。 若一个点不在线段的垂直平分线上,则它到这条线段两端点的距离不相等。若两个角不相等,则它们不是对顶角。4.写出下列各命题的逆命题,否命题,逆否命题,并判断其真假
(1)如果x≧5,那么x≧2
(2)如果一个函数是偶函数,则它的图像关于y轴成轴对称图形。
提升原命题的真假和它的否命题,逆命题,逆否命
题之间的真假分别有什么关系?原命题与它的逆命题,原命题和它的否命题之间的真假是不定的,而原命题和它的逆否命题之间在真假上始终保持一致的:同真或同假。
即:互为逆否的两个命题等价
互逆或互否的两个命题不等价小结:
四种命题的转换方法
(1)交换原命题的条件和结论,所得命题是原命题的逆命题.
(2)同时否定原命题的条件和结论,所得命题是原命题的否命题.
(3)交换原命题的条件和结论,并且同时否定,所得命题是原命题的逆否命题.
根据学习本节的知识提高自己的解决问题的能力。
作业:
习题1-3A 2、3、5
