圆锥面与圆锥曲线 课件(23张PPT)
文档属性
| 名称 | 圆锥面与圆锥曲线 课件(23张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 11.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 00:00:00 | ||
图片预览







文档简介
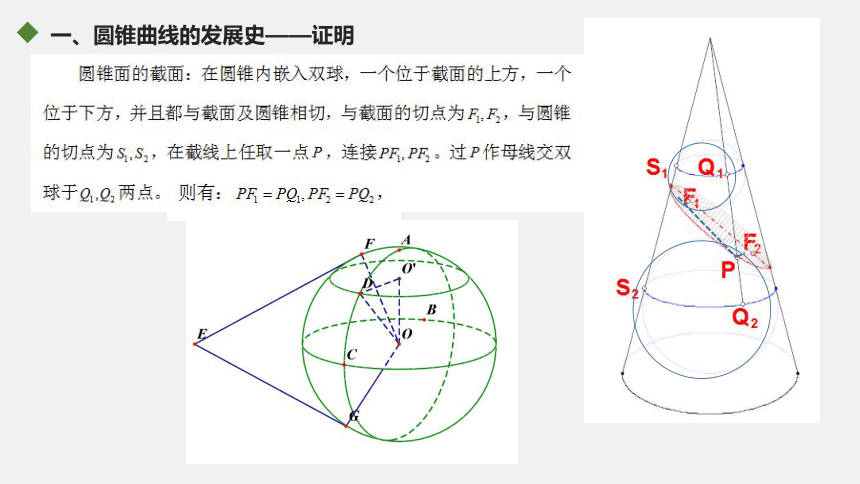
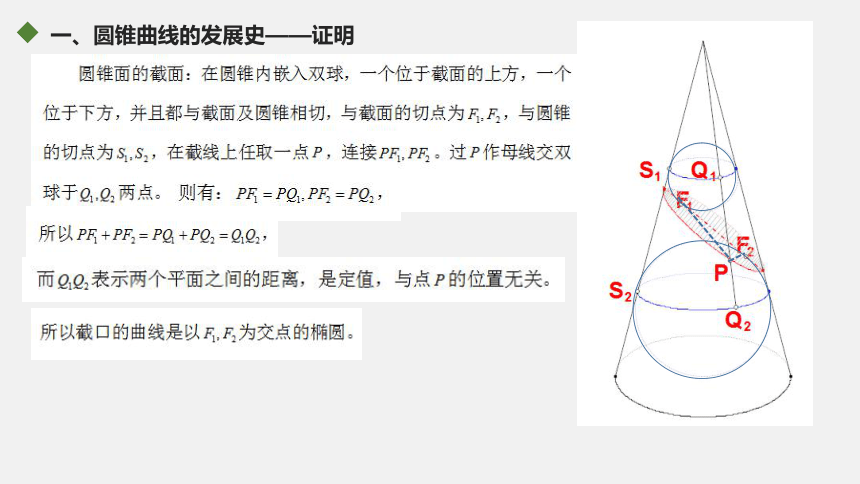
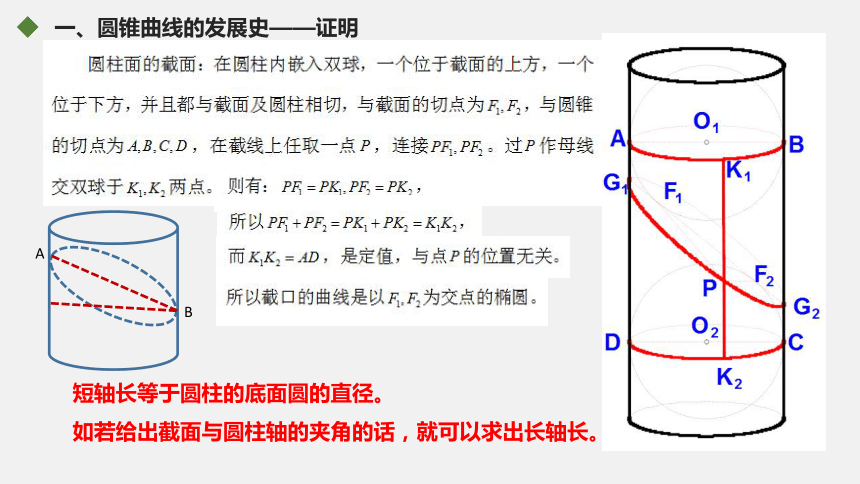
课件33张PPT。圆锥面与圆锥曲线2018应用:目 录1圆锥曲线的发展史2二元二次方程与圆锥曲线3圆锥曲线的光学性质圆锥曲线发展史——预习检测——历史人物最先发现圆锥曲线的数学家是古希腊的( )揭示出行星按椭圆轨道环绕太阳运行的天文学家是( )得出物体斜抛运动的轨道是抛物线的物理学家是( )创立解析几何的法国数学家是( )《圆锥曲线论》的作者是( )A.开普勒 B.阿波罗尼奥斯 C.伽利略 D.笛卡尔 E.梅内赫莫斯 F.欧几里得 G.阿基米德 E CA DB一、圆锥曲线的发展史——梅内赫莫斯梅内赫莫斯古希腊三大作图问题一、圆锥曲线的发展史 梅内赫莫斯欧几里得阿基米德阿波罗尼奥斯《圆锥曲线论》动画演示一、圆锥曲线的发展史——阿波罗尼奥斯lmA一、圆锥曲线的发展史——动画演示一、圆锥曲线的发展史——证明一、圆锥曲线的发展史——证明一、圆锥曲线的发展史——证明短轴长等于圆柱的底面圆的直径。
如若给出截面与圆柱轴的夹角的话,就可以求出长轴长。AB一、圆锥曲线的发展史——证明——练习:CD 阿波罗尼奥斯二、二元二次方程与圆锥曲线 开普勒
揭示出行星按椭圆轨道运行 伽利略
物体斜抛运动的轨道是抛物线 笛卡尔
创立解析几何 欧拉
《无穷小分析引论》 坐标研究时代
二元二次方程b控制图形是否旋转(d,e)图形中心的位置a=c可能为圆a,c不等可能为椭圆,双曲线等二、二元二次方程与圆锥曲线二、二元二次方程与圆锥曲线经过适当的坐标变换,可以化为以下标准形式之一:二、二元二次方程与圆锥曲线经过适当的坐标变换,可以化为以下标准形式之一:1234K取何值时,方程的曲线是抛物线?二、二元二次方程与圆锥曲线-例题分析:K取何值时,方程的曲线是椭圆?K取何值时,方程的曲线是圆?K取何值时,方程的曲线是双曲线?演示结论应用证明三、圆锥曲线的光学性质——抛物线结论:三、圆锥曲线的光学性质——抛物线通过演示,可以看到,当灯泡位置处在抛物线焦点位置时,反射光线平行于抛物线的轴。根据光线的可逆性可知,平行于抛物线的轴的光线照射到抛物线上,经反射后都通过焦点。.三、圆锥曲线的光学性质——抛物线应用平行的照射出去反射后,经过焦点三、圆锥曲线的光学性质——抛物线证明演示结论应用三、圆锥曲线的光学性质——椭圆结论:三、圆锥曲线的光学性质——椭圆从椭圆的一个焦点处发出的光,
经过椭圆反射后,
反射光线通过椭圆的另一个焦点。三、圆锥曲线的光学性质——椭圆应用:平行的照射出去激光消痣与体外碎石技术三、圆锥曲线的光学性质——椭圆应用平行的照射出去演示结论应用双曲线三、圆锥曲线的光学性质——双曲线结论:三、圆锥曲线的光学性质——双曲线从双曲线的一个焦点处发出的光线照射到
双曲线上,反射光线是散开,但是,
反射光线的反向延长线交于另一个焦点上。
光线就好像从另一个焦点射出的一样。反射式天文望远镜三、圆锥曲线的光学性质——双曲线应用转角镜 后视镜三、圆锥曲线的光学性质—例题:作业: 1将圆锥曲线的光学性质进行组合,尝试设计一些作品?2可以用光学性质解决一些高考试题吗?收获: 思维导图
如若给出截面与圆柱轴的夹角的话,就可以求出长轴长。AB一、圆锥曲线的发展史——证明——练习:CD 阿波罗尼奥斯二、二元二次方程与圆锥曲线 开普勒
揭示出行星按椭圆轨道运行 伽利略
物体斜抛运动的轨道是抛物线 笛卡尔
创立解析几何 欧拉
《无穷小分析引论》 坐标研究时代
二元二次方程b控制图形是否旋转(d,e)图形中心的位置a=c可能为圆a,c不等可能为椭圆,双曲线等二、二元二次方程与圆锥曲线二、二元二次方程与圆锥曲线经过适当的坐标变换,可以化为以下标准形式之一:二、二元二次方程与圆锥曲线经过适当的坐标变换,可以化为以下标准形式之一:1234K取何值时,方程的曲线是抛物线?二、二元二次方程与圆锥曲线-例题分析:K取何值时,方程的曲线是椭圆?K取何值时,方程的曲线是圆?K取何值时,方程的曲线是双曲线?演示结论应用证明三、圆锥曲线的光学性质——抛物线结论:三、圆锥曲线的光学性质——抛物线通过演示,可以看到,当灯泡位置处在抛物线焦点位置时,反射光线平行于抛物线的轴。根据光线的可逆性可知,平行于抛物线的轴的光线照射到抛物线上,经反射后都通过焦点。.三、圆锥曲线的光学性质——抛物线应用平行的照射出去反射后,经过焦点三、圆锥曲线的光学性质——抛物线证明演示结论应用三、圆锥曲线的光学性质——椭圆结论:三、圆锥曲线的光学性质——椭圆从椭圆的一个焦点处发出的光,
经过椭圆反射后,
反射光线通过椭圆的另一个焦点。三、圆锥曲线的光学性质——椭圆应用:平行的照射出去激光消痣与体外碎石技术三、圆锥曲线的光学性质——椭圆应用平行的照射出去演示结论应用双曲线三、圆锥曲线的光学性质——双曲线结论:三、圆锥曲线的光学性质——双曲线从双曲线的一个焦点处发出的光线照射到
双曲线上,反射光线是散开,但是,
反射光线的反向延长线交于另一个焦点上。
光线就好像从另一个焦点射出的一样。反射式天文望远镜三、圆锥曲线的光学性质——双曲线应用转角镜 后视镜三、圆锥曲线的光学性质—例题:作业: 1将圆锥曲线的光学性质进行组合,尝试设计一些作品?2可以用光学性质解决一些高考试题吗?收获: 思维导图
