3.3.2 利用导数研究函数的极值 课件(32张PPT)
文档属性
| 名称 | 3.3.2 利用导数研究函数的极值 课件(32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 600.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 00:00:00 | ||
图片预览










文档简介
课件32张PPT。导数与函数的极值和最值基础知识梳理1.函数的极值
(1)函数的极值的概念:
函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;而且在点x=a附近的左侧 ,右侧 ,则点a叫做函数y=f(x)的 ,f(a)叫做函数y=f(x)的 .f′(x)<0f′(x)>0极小值点极小值基础知识梳理 函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;而且在点x=b附近的左侧 ,
右侧 ,则点b叫做函数y=f(x)的 ,f(b)叫做函数y=f(x)的 .极小值点、极大值点统称为 ,极大值和极小值统称为 .f′(x)>0f′(x)<0极大值点极大值极值点极值基础知识梳理(2)求函数极值的步骤:
① ;
② ;
③检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取 ,如果左负右正,那么f(x)在这个根处取 .求导数f′(x)求方程f′(x)=0的根极大值极小值基础知识梳理方程f′(x)=0的根就是函数y=f(x)的极值点是否正确?
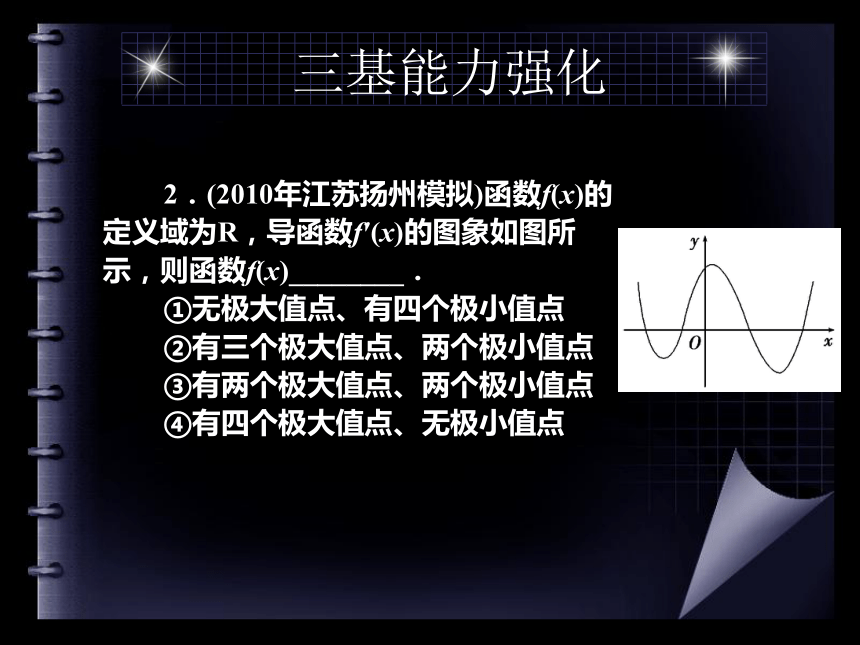
【思考·提示】 不正确,方程f′(x)=0的根未必都是极值点.如函数f(x)=x3思考?三基能力强化1.函数f(x)=2x3-3x2+a的极大值是6,求a的值三基能力强化2.(2010年江苏扬州模拟)函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)________.
①无极大值点、有四个极小值点
②有三个极大值点、两个极小值点
③有两个极大值点、两个极小值点
④有四个极大值点、无极小值点三基能力强化解析:设f′(x)与x轴的4个交点,从左至右依次为x1、x2、x3、x4.
当x0,f(x)为增函数,
当x1则x=x1为极大值点,
同理,x=x3为极大值点,
x=x2,x=x4为极小值点.
答案:③三基能力强化3.已知f(x)=ax3+bx2+x(a,b∈R且ab≠0)的图象如图所示,且|x1|>|x2|,则有a,b的正负情况是________.答案:a<0,b<0三基能力强化4.函数f(x)=x3+3ax2+3[(a+2)x+1]既有极大值又有极小值,则a的取值范围是________.
解析:f′(x)=3x2+6ax+3(a+2),令3x2+6ax+3(a+2)=0,即x2+2ax+a+2=0.因为函数f(x)有极大值和极小值,所以方程x2+2ax+a+2=0有两个不相等的实根,即Δ=4a2-4a-8>0,解得a>2或a<-1.
答案:a>2或a<-1课堂互动讲练极值是一个局部概念,极值的大小关系是不确定的,即极大值不一定比极小值大,极小值也不一定比极大值小.极值在区间端点处不存在.课堂互动讲练(2009年高考北京卷)设函数f(x)=x3-3ax+b(a≠0).
(1)若曲线y=f(x)在点(2,f(2))处与直线y=8相切,求a,b的值;
(2)求函数f(x)的单调区间与极值点.【思路点拨】 (1)由f′(2)=0,f(2)=8求a,b;(2)求f′(x),讨论单调性.课堂互动讲练【解】 (1)f′(x)=3x2-3a.
因为曲线y=f(x)在点(2,f(2))处与直线y=8相切,
所以
解得a=4,b=24.(2)f′(x)=3(x2-a)(a≠0).
当a<0时,f′(x)>0,函数f(x)在(-∞, +∞)上单调递增;此时函数f(x)没有极值点.课堂互动讲练课堂互动讲练【点评】 求函数的极值,与研究函数的单调性的过程是一致的,为使思路清晰,可以严格按照求极值的步骤来推理,最好以列表格的形式来体现,对含参数的问题,要注意引起讨论的原因再分类讨论.
极值问题有一类逆向思维的题,即已知函数极值求参数的值,此类题目要充分利用f′(x0)=0这个条件,其次也要注意单调性对极值的限制.课堂互动讲练1.(2009年高考四川卷)已知函数f(x)=x3+2bx2+cx-2的图象在与x轴交点处的切线方程是y=5x-10.
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+ mx,若g(x)的极值存在,求实数m的取值范围以及函数g(x)取得极值时对应的自变量x的值. 跟踪训练课堂互动讲练解:(1)由已知,得切点为(2,0),
故有f(2)=0,即4b+c+3=0.①
f′(x)=3x2+4bx+c,由已知,得
f′(2)=12+8b+c=5.
得8b+c+7=0.②
联立①、②,解得c=1,b=-1,
于是函数解析式为f(x)=x3-2x2+x-2. 跟踪训练课堂互动讲练 跟踪训练课堂互动讲练 跟踪训练课堂互动讲练 跟踪训练课堂互动讲练2、 已知f(x)= ax3+bx2+cx (a≠0)在x=±1时取得极值,且f(1)=-1,
(1)试求常数a、b、c的值;
(2)试判断x=±1时函数取得极小值还是极大值,并说明理由.
?
互动探究a=0.5,b=0,c=-1,5;x=-1是极大值点,x=1是极小值点课堂互动讲练本类题主要是指函数方程根的个数或两函数图象交点个数问题,常用构造函数的方法,转化为研究函数极值及图象的相关问题.课堂互动讲练(2009年高考陕西卷)已知函数f(x)=x3-3ax-1,a≠0.
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,求m的取值范围.课堂互动讲练【思路点拨】 (1)求f′(x),讨论a;(2)由f′(-1)=0,求出a,求f(x)的极值,观察图象,求m的范围.【解】 (1)f′(x)=3x2-3a=3(x2-a),
当a<0时,对x∈R,有f′(x)>0,
∴当a<0时,f(x)的单调增区间为(-∞,+∞).课堂互动讲练课堂互动讲练(2)∵f(x)在x=-1处取得极值,
∴f′(-1)=3×(-1)2-3a=0,∴a=1.
∴f(x)=x3-3x-1,f′(x)=3x2-3,
由f′(x)=0解得x1=-1,x2=1.
由(1)中f(x)的单调性可知,f(x)在x=-1处取得极大值f(-1)=1,在x=1处取得极小值f(1)=-3.
∵直线y=m与函数y=f(x)的图象有三个不同的交点,
又f(-3)=-19<-3,f(3)=17>1,结合f(x)的单调性可知,m的取值范围是(-3,1).课堂互动讲练【点评】 用求导的方法确定方程根的个数,是一种很有效的方法.它首先通过求导,明确函数的单调性以及函数的极值,然后粗略地画出函数的图象,根据函数的变化情况,运用数形结合的思想来确定函数图象与x轴的交点个数.课堂互动讲练3.例2条件不变,若函数f(x)与x轴有三个不同的交点,求a的取值范围.(只写出限制条件不必计算出结果) 互动探究规律方法总结1.可导函数的极值
(1)极值是一个局部性概念,一个函数在其定义域内可以有许多个极大值和极小值,在某一点的极小值也可能大于另一点的极大值,也就是说极大值与极小值没有必然的大小关系.
(2)若f(x)在(a,b)内有极值,那么f(x)在(a,b)内绝不是单调函数,即在某区间上单调递增或减的函数没有极值.规律方法总结2.函数的最大值和最小值是一个整体性概念,最大值必须是整个区间上所有函数值中的最大值,最小值必须是整个区间上所有函数值中的最小值.规律方法总结3.函数的最大值、最小值是比较整个定义区间的函数值得出来的,函数的极值是比较极值点附近的函数值得出来的.函数的极值可以有多有少,但最值只有一个;极值只能在区间内取得,最值则可以在端点处取得;有极值的未必有最值,有最值的未必有极值;极值可能成为最值,最值只要不在端点必定是极值.再见
(1)函数的极值的概念:
函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;而且在点x=a附近的左侧 ,右侧 ,则点a叫做函数y=f(x)的 ,f(a)叫做函数y=f(x)的 .f′(x)<0f′(x)>0极小值点极小值基础知识梳理 函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;而且在点x=b附近的左侧 ,
右侧 ,则点b叫做函数y=f(x)的 ,f(b)叫做函数y=f(x)的 .极小值点、极大值点统称为 ,极大值和极小值统称为 .f′(x)>0f′(x)<0极大值点极大值极值点极值基础知识梳理(2)求函数极值的步骤:
① ;
② ;
③检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取 ,如果左负右正,那么f(x)在这个根处取 .求导数f′(x)求方程f′(x)=0的根极大值极小值基础知识梳理方程f′(x)=0的根就是函数y=f(x)的极值点是否正确?
【思考·提示】 不正确,方程f′(x)=0的根未必都是极值点.如函数f(x)=x3思考?三基能力强化1.函数f(x)=2x3-3x2+a的极大值是6,求a的值三基能力强化2.(2010年江苏扬州模拟)函数f(x)的定义域为R,导函数f′(x)的图象如图所示,则函数f(x)________.
①无极大值点、有四个极小值点
②有三个极大值点、两个极小值点
③有两个极大值点、两个极小值点
④有四个极大值点、无极小值点三基能力强化解析:设f′(x)与x轴的4个交点,从左至右依次为x1、x2、x3、x4.
当x
当x1
同理,x=x3为极大值点,
x=x2,x=x4为极小值点.
答案:③三基能力强化3.已知f(x)=ax3+bx2+x(a,b∈R且ab≠0)的图象如图所示,且|x1|>|x2|,则有a,b的正负情况是________.答案:a<0,b<0三基能力强化4.函数f(x)=x3+3ax2+3[(a+2)x+1]既有极大值又有极小值,则a的取值范围是________.
解析:f′(x)=3x2+6ax+3(a+2),令3x2+6ax+3(a+2)=0,即x2+2ax+a+2=0.因为函数f(x)有极大值和极小值,所以方程x2+2ax+a+2=0有两个不相等的实根,即Δ=4a2-4a-8>0,解得a>2或a<-1.
答案:a>2或a<-1课堂互动讲练极值是一个局部概念,极值的大小关系是不确定的,即极大值不一定比极小值大,极小值也不一定比极大值小.极值在区间端点处不存在.课堂互动讲练(2009年高考北京卷)设函数f(x)=x3-3ax+b(a≠0).
(1)若曲线y=f(x)在点(2,f(2))处与直线y=8相切,求a,b的值;
(2)求函数f(x)的单调区间与极值点.【思路点拨】 (1)由f′(2)=0,f(2)=8求a,b;(2)求f′(x),讨论单调性.课堂互动讲练【解】 (1)f′(x)=3x2-3a.
因为曲线y=f(x)在点(2,f(2))处与直线y=8相切,
所以
解得a=4,b=24.(2)f′(x)=3(x2-a)(a≠0).
当a<0时,f′(x)>0,函数f(x)在(-∞, +∞)上单调递增;此时函数f(x)没有极值点.课堂互动讲练课堂互动讲练【点评】 求函数的极值,与研究函数的单调性的过程是一致的,为使思路清晰,可以严格按照求极值的步骤来推理,最好以列表格的形式来体现,对含参数的问题,要注意引起讨论的原因再分类讨论.
极值问题有一类逆向思维的题,即已知函数极值求参数的值,此类题目要充分利用f′(x0)=0这个条件,其次也要注意单调性对极值的限制.课堂互动讲练1.(2009年高考四川卷)已知函数f(x)=x3+2bx2+cx-2的图象在与x轴交点处的切线方程是y=5x-10.
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+ mx,若g(x)的极值存在,求实数m的取值范围以及函数g(x)取得极值时对应的自变量x的值. 跟踪训练课堂互动讲练解:(1)由已知,得切点为(2,0),
故有f(2)=0,即4b+c+3=0.①
f′(x)=3x2+4bx+c,由已知,得
f′(2)=12+8b+c=5.
得8b+c+7=0.②
联立①、②,解得c=1,b=-1,
于是函数解析式为f(x)=x3-2x2+x-2. 跟踪训练课堂互动讲练 跟踪训练课堂互动讲练 跟踪训练课堂互动讲练 跟踪训练课堂互动讲练2、 已知f(x)= ax3+bx2+cx (a≠0)在x=±1时取得极值,且f(1)=-1,
(1)试求常数a、b、c的值;
(2)试判断x=±1时函数取得极小值还是极大值,并说明理由.
?
互动探究a=0.5,b=0,c=-1,5;x=-1是极大值点,x=1是极小值点课堂互动讲练本类题主要是指函数方程根的个数或两函数图象交点个数问题,常用构造函数的方法,转化为研究函数极值及图象的相关问题.课堂互动讲练(2009年高考陕西卷)已知函数f(x)=x3-3ax-1,a≠0.
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,求m的取值范围.课堂互动讲练【思路点拨】 (1)求f′(x),讨论a;(2)由f′(-1)=0,求出a,求f(x)的极值,观察图象,求m的范围.【解】 (1)f′(x)=3x2-3a=3(x2-a),
当a<0时,对x∈R,有f′(x)>0,
∴当a<0时,f(x)的单调增区间为(-∞,+∞).课堂互动讲练课堂互动讲练(2)∵f(x)在x=-1处取得极值,
∴f′(-1)=3×(-1)2-3a=0,∴a=1.
∴f(x)=x3-3x-1,f′(x)=3x2-3,
由f′(x)=0解得x1=-1,x2=1.
由(1)中f(x)的单调性可知,f(x)在x=-1处取得极大值f(-1)=1,在x=1处取得极小值f(1)=-3.
∵直线y=m与函数y=f(x)的图象有三个不同的交点,
又f(-3)=-19<-3,f(3)=17>1,结合f(x)的单调性可知,m的取值范围是(-3,1).课堂互动讲练【点评】 用求导的方法确定方程根的个数,是一种很有效的方法.它首先通过求导,明确函数的单调性以及函数的极值,然后粗略地画出函数的图象,根据函数的变化情况,运用数形结合的思想来确定函数图象与x轴的交点个数.课堂互动讲练3.例2条件不变,若函数f(x)与x轴有三个不同的交点,求a的取值范围.(只写出限制条件不必计算出结果) 互动探究规律方法总结1.可导函数的极值
(1)极值是一个局部性概念,一个函数在其定义域内可以有许多个极大值和极小值,在某一点的极小值也可能大于另一点的极大值,也就是说极大值与极小值没有必然的大小关系.
(2)若f(x)在(a,b)内有极值,那么f(x)在(a,b)内绝不是单调函数,即在某区间上单调递增或减的函数没有极值.规律方法总结2.函数的最大值和最小值是一个整体性概念,最大值必须是整个区间上所有函数值中的最大值,最小值必须是整个区间上所有函数值中的最小值.规律方法总结3.函数的最大值、最小值是比较整个定义区间的函数值得出来的,函数的极值是比较极值点附近的函数值得出来的.函数的极值可以有多有少,但最值只有一个;极值只能在区间内取得,最值则可以在端点处取得;有极值的未必有最值,有最值的未必有极值;极值可能成为最值,最值只要不在端点必定是极值.再见
