1.3 勾股定理的应用(要点讲解+当堂检测+答案)
文档属性
| 名称 | 1.3 勾股定理的应用(要点讲解+当堂检测+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-23 20:26:48 | ||
图片预览


文档简介
北师大版数学八年级上册同步学案
第一章 勾股定理
3 勾股定理的应用
要 点 讲 解
要点一 确定几何体上的最短路线
1. 柱体和长方体的展开图是一个长方形.
2. 求柱体或长方体上两点之间最短距离,需要把柱体或长方体展开成平面图形,依据两点之间线段最短,以最短路线为边构造成直角三角形,再利用勾股定理求解.
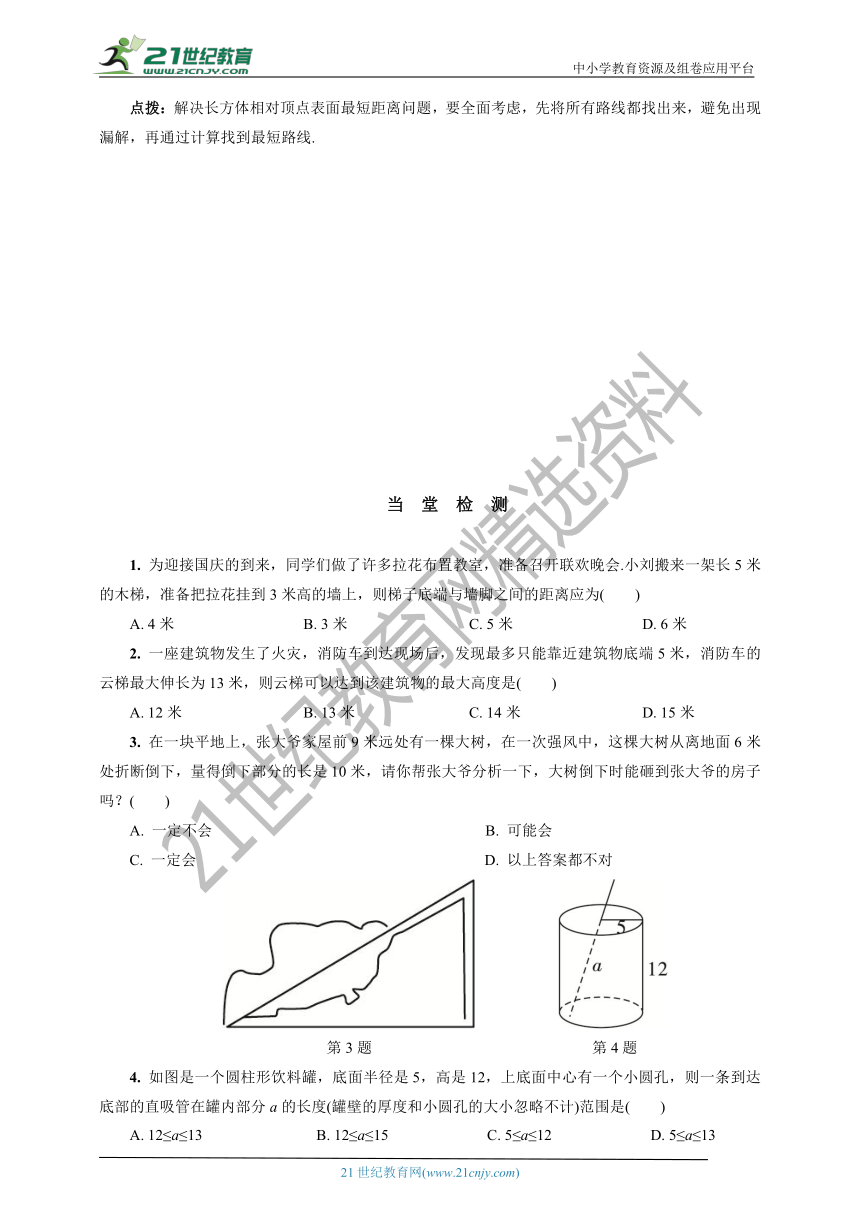
经典例题1 有一个圆柱形油罐,如图所示,要从A点环绕油罐建梯子,正好到A点的正上方B点,问梯子最短需要多长?(已知油罐的底面周长是12m,高AB是5m)
解:将圆柱形油罐的侧面沿AB剪开展成一个平面图形,如图所示,沿AB′建梯子最节省材料(两点之间,线段最短).由已知得AB=5m,BB′=12m.在Rt△ABB′中,AB′2=AB2+BB′2=52+122=132(m2),所以AB′=13m.因此所建的梯子最短需要13m.
点拨:由于梯子要绕着曲面建,因此最短路线应将曲面展成平面后,再依据“两点之间,线段最短”来确定.
要点二 利用勾股定理解决生活中的长度问题
1. 由勾股定理的知识,可以解决与直角三角形相关的一些实际问题.在解决实际问题时,应具体问题具体分析,将生活中的问题转化为数学问题,利用勾股定理加以解决.
2. 勾股定理的逆定理主要用来说明一个三角形为直角三角形.在实际问题中,有些线段的求解、角的求解在很大程度上转化为在直角三角形内求解.因此,熟练地判断一个三角形是否为直角三角形是首先要解决的问题.
经典例题2 小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度.
解析:根据题意寻找出绳子长度与旗杆高度之间的关系,设未知数,利用勾股定理构造方程.解方程求得结论.
解:设旗杆高x米,则绳长(x+1)米.依题意,得x2+52=(x+1)2,解得x=12.即旗杆的高度为12米.
易错易混警示 将长方体展开时,忽视展开方式不唯一
对长方体来说,由于一般情况下,长、宽、高不相等,则展开得到的距离也不相同,故对此问题应把可能出现的情况考虑全,分别计算,经过比较求出最短距离.
经典例题3 有一个长方体纸盒,如图所示,小明所在数学小组研究由长方体的底面A点到长方体中与A点相对的B点的最短距离,若长方体的底面长为12,宽为9,高为5,请帮助该小组求出由A点到B点的最短距离.(参考数据:21.592≈466,19.242≈370,18.442≈340)
解:将四边形ACDF与四边形DCEB展开在同一平面,如图(1)所示.在Rt△ABE中,由勾股定理,得AB2=AE2+BE2=(12+9)2+52=466;
同理,由图(2),得AB2=AC2+BC2=122+(9+5)2=340;
由图(3),得AB2=AD2+BD2=(12+5)2+92=370.
因为340<370<466,所以最短距离为图(2)所示线段AB的长度,AB≈18.44.
图(1) 图(2) 图(3)
点拨:解决长方体相对顶点表面最短距离问题,要全面考虑,先将所有路线都找出来,避免出现漏解,再通过计算找到最短路线.
当 堂 检 测
1. 为迎接国庆的到来,同学们做了许多拉花布置教室,准备召开联欢晚会.小刘搬来一架长5米的木梯,准备把拉花挂到3米高的墙上,则梯子底端与墙脚之间的距离应为( )
A. 4米 B. 3米 C. 5米 D. 6米
2. 一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大伸长为13米,则云梯可以达到该建筑物的最大高度是( )
A. 12米 B. 13米 C. 14米 D. 15米
3. 在一块平地上,张大爷家屋前9米远处有一棵大树,在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米,请你帮张大爷分析一下,大树倒下时能砸到张大爷的房子吗?( )
A. 一定不会 B. 可能会
C. 一定会 D. 以上答案都不对
第3题 第4题
4. 如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A. 12≤a≤13 B. 12≤a≤15 C. 5≤a≤12 D. 5≤a≤13
5. 如图,长方体的高为3cm,底面是边长为2cm的正方形,现用绳子从A开始缠绕,沿长方体表面经BD到达C处,则需要绳子的最短长度是( )
A. 4cm B. 5cm C. 5.5cm D. 6cm
第5题 第6题
6. 如图,一个游泳爱好者要横跨一条宽AC=8m的河流,由于水流速度的原因,这位游泳爱好者向下游偏离了BC=6m,这位游泳爱好者在横跨河流时的实际游泳距离为 m.
7. 有一个圆柱,它的高为9厘米,底面周长为24厘米,在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物,问它爬行的最短路程是多少厘米?
当堂检测参考答案
1. A 2. A 3. A 4. A 5. B
6. 10
7. 解:画圆柱侧面展开图如图,依题意得AD=12厘米,BD=9厘米,在Rt△ABD中,AB2=BD2+
第一章 勾股定理
3 勾股定理的应用
要 点 讲 解
要点一 确定几何体上的最短路线
1. 柱体和长方体的展开图是一个长方形.
2. 求柱体或长方体上两点之间最短距离,需要把柱体或长方体展开成平面图形,依据两点之间线段最短,以最短路线为边构造成直角三角形,再利用勾股定理求解.
经典例题1 有一个圆柱形油罐,如图所示,要从A点环绕油罐建梯子,正好到A点的正上方B点,问梯子最短需要多长?(已知油罐的底面周长是12m,高AB是5m)
解:将圆柱形油罐的侧面沿AB剪开展成一个平面图形,如图所示,沿AB′建梯子最节省材料(两点之间,线段最短).由已知得AB=5m,BB′=12m.在Rt△ABB′中,AB′2=AB2+BB′2=52+122=132(m2),所以AB′=13m.因此所建的梯子最短需要13m.
点拨:由于梯子要绕着曲面建,因此最短路线应将曲面展成平面后,再依据“两点之间,线段最短”来确定.
要点二 利用勾股定理解决生活中的长度问题
1. 由勾股定理的知识,可以解决与直角三角形相关的一些实际问题.在解决实际问题时,应具体问题具体分析,将生活中的问题转化为数学问题,利用勾股定理加以解决.
2. 勾股定理的逆定理主要用来说明一个三角形为直角三角形.在实际问题中,有些线段的求解、角的求解在很大程度上转化为在直角三角形内求解.因此,熟练地判断一个三角形是否为直角三角形是首先要解决的问题.
经典例题2 小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度.
解析:根据题意寻找出绳子长度与旗杆高度之间的关系,设未知数,利用勾股定理构造方程.解方程求得结论.
解:设旗杆高x米,则绳长(x+1)米.依题意,得x2+52=(x+1)2,解得x=12.即旗杆的高度为12米.
易错易混警示 将长方体展开时,忽视展开方式不唯一
对长方体来说,由于一般情况下,长、宽、高不相等,则展开得到的距离也不相同,故对此问题应把可能出现的情况考虑全,分别计算,经过比较求出最短距离.
经典例题3 有一个长方体纸盒,如图所示,小明所在数学小组研究由长方体的底面A点到长方体中与A点相对的B点的最短距离,若长方体的底面长为12,宽为9,高为5,请帮助该小组求出由A点到B点的最短距离.(参考数据:21.592≈466,19.242≈370,18.442≈340)
解:将四边形ACDF与四边形DCEB展开在同一平面,如图(1)所示.在Rt△ABE中,由勾股定理,得AB2=AE2+BE2=(12+9)2+52=466;
同理,由图(2),得AB2=AC2+BC2=122+(9+5)2=340;
由图(3),得AB2=AD2+BD2=(12+5)2+92=370.
因为340<370<466,所以最短距离为图(2)所示线段AB的长度,AB≈18.44.
图(1) 图(2) 图(3)
点拨:解决长方体相对顶点表面最短距离问题,要全面考虑,先将所有路线都找出来,避免出现漏解,再通过计算找到最短路线.
当 堂 检 测
1. 为迎接国庆的到来,同学们做了许多拉花布置教室,准备召开联欢晚会.小刘搬来一架长5米的木梯,准备把拉花挂到3米高的墙上,则梯子底端与墙脚之间的距离应为( )
A. 4米 B. 3米 C. 5米 D. 6米
2. 一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大伸长为13米,则云梯可以达到该建筑物的最大高度是( )
A. 12米 B. 13米 C. 14米 D. 15米
3. 在一块平地上,张大爷家屋前9米远处有一棵大树,在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米,请你帮张大爷分析一下,大树倒下时能砸到张大爷的房子吗?( )
A. 一定不会 B. 可能会
C. 一定会 D. 以上答案都不对
第3题 第4题
4. 如图是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
A. 12≤a≤13 B. 12≤a≤15 C. 5≤a≤12 D. 5≤a≤13
5. 如图,长方体的高为3cm,底面是边长为2cm的正方形,现用绳子从A开始缠绕,沿长方体表面经BD到达C处,则需要绳子的最短长度是( )
A. 4cm B. 5cm C. 5.5cm D. 6cm
第5题 第6题
6. 如图,一个游泳爱好者要横跨一条宽AC=8m的河流,由于水流速度的原因,这位游泳爱好者向下游偏离了BC=6m,这位游泳爱好者在横跨河流时的实际游泳距离为 m.
7. 有一个圆柱,它的高为9厘米,底面周长为24厘米,在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物,问它爬行的最短路程是多少厘米?
当堂检测参考答案
1. A 2. A 3. A 4. A 5. B
6. 10
7. 解:画圆柱侧面展开图如图,依题意得AD=12厘米,BD=9厘米,在Rt△ABD中,AB2=BD2+
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
