数学必修三第三章第一节,随机事件的概率比赛课件 (共17张PPT)-北师大版
文档属性
| 名称 | 数学必修三第三章第一节,随机事件的概率比赛课件 (共17张PPT)-北师大版 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
北师大版《普通高中课程标准实验教科书》·数学·必修三
随机事件的概率
(第一课时)
一、创设情境,引入新知
生活实例:张梦雪里约奥运夺首金
一、创设情境,引入新知
生活实例2:女排逆转夺冠
一、创设情境,引入新知
思考一:
1、在张梦雪射击前,你能知道她会获得冠军吗?
2、在比赛前,你能猜到中国女排能夺得金牌吗?
一、创设情境,引入新知
思考二:
1、既然能否夺冠是随机事件,为什么派张梦雪参加奥运会,而不是派其他射击运动员参加?
2、张梦雪“击中靶心的可能性比其他射击运动员大”这一生活经验是如何得到的呢?
在生活中我们通常用射击试验命中的频率来估计命中的概率,那么这种方法是否具有普遍性?
(一)动手试验,探究随机事件的可能性大小
二、合作交流,探究新知
(1)试验目的:探究随机事件“抛掷一枚硬币,正面向上”的可能性大小.
(2)试验要求:
①假设硬币的材质是均匀的,所有的硬币都相同;
②从离桌面大约30cm的高度,让其自由下落在桌面上;
③5人一组,每人抛掷20次,共100次,各自认真记录 “正面向上”出现的次数,组长汇总本组的总次数.
认真阅读
二、合作交流,探究新知
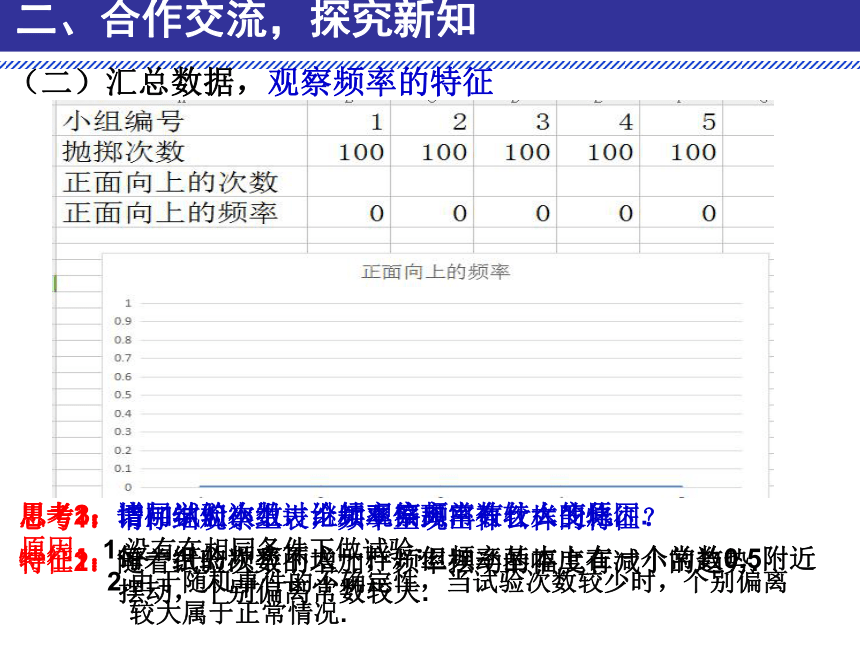
(二)汇总数据,观察频率的特征
思考1:请仔细观察上表,频率呈现出什么样的特征?
特征1:每一组的频率不太一样,但频率基本上在一个常数0.5附近
摆动,个别偏离常数较大.
思考2:请同学们小组讨论频率偏离常数较大的原因.
原因:1.没有在相同条件下做试验;
2.由于随机事件的不确定性,当试验次数较少时,个别偏离
较大属于正常情况.
思考3:增加试验次数,继续观察频率有什么变化.
特征2:随着试验次数的增加,频率摆动的幅度有减小的趋势.
二、合作交流,探究新知
(三)观察分析,探究频率的规律性
特征2:随着试验次数的增加,频率摆动的幅度有减小的趋势,并
逐渐稳定于常数0.5.
二、合作交流,探究新知
(三)观察分析,探究频率的规律性
思考:
①能不能用某次试验的频率作为硬币正面向上的概率?
②用哪个量作为硬币正面向上的概率比较合适呢?
结论:在相同条件下,大量重复抛掷硬币时,出现正面向上的频率会在常数0.5附近摆动,随着试验次数的增加,正面向上的频率稳定于常数0.5 ,这个常数0.5就是正面向上的概率.
试验者 抛掷次数n 正面向上的次数m 频率m/n
德·摩根 2048 1061 0.5181
蒲丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 24000 12012 0.5005
罗曼诺夫斯基 80640 40173 0.4982
二、合作交流,探究新知
(四)感知升华,概括结论
试验结论:在相同条件下,大量重复抛掷硬币试验时,出现正面向上的频率在常数0.5附近摆动,随着试验次数的增加,正面向上的频率稳定于常数0.5,这个常数0.5就是硬币正面向上的概率.
请同学们根据试验结论,尝试自己概括出概率的统计定义.
二、合作交流,探究新知
1.概率的统计定义
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率会在某一个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,我们把这个常数叫做随机事件A的概率,记作P(A).
(四)感知升华,概括结论
思考:随机事件A的概率 P(A)的取值范围是多少?随机事件的概率可以为0或1吗?你能举例说明吗?
二、合作交流,探究新知
1.概率的统计定义
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率会在某一个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,我们把这个常数叫做随机事件A的概率,记作P(A).
(四)感知升华,概括结论
范围:0≤P(A) ≤1.
如:大家都知道《守株待兔》这个成语故事,你会像故事中的农夫那样坐在树底下“待兔”吗?为什么?
大量重复试验
2.求随机事件概率的方法
二、合作交流,探究新知
3.“概率”和“频率”的区别与联系
(四)感知升华,概括结论
区别:频率反映了随机事件出现的频繁程度,是随机性
的;概率是确定的,是客观存在的,与试验无关.
联系:频率是概率的近似值,概率是频率的稳定值.
(1)在对一批种子进行的发芽试验中,抽取的10粒种子全部发芽,所以该种子的发芽率为100%;
(2)乒乓球比赛中,小李比小王获胜的概率大,若两人打一局比赛,小李一定获胜;
(3)因为抛掷一枚硬币出现正面的概率是0.5,所以抛掷12000次时,出现正面的次数很有可能接近6000次;
(4)某种彩票中奖的概率为 ,那么买1000张彩票一定能
中奖.
例1.判断下列说法的对错:
三、自主练习,应用新知
?
?
?
?
例2.某射手在同一条件下进行射击,结果如下:
0.90
0.93
0.88
0.92
0.89
0.91
(1)计算表中击中靶心的各个频率;
(2)这个射手射击一次,击中靶心的概率约为多少?
三、自主练习,应用新知
0.90
射击次数n 10 30 50 100 200 500
击中靶心的次数 m 9 28 44 92 178 455
击中靶心的频率m/n
四、课堂小结,再现新知
通过本节课的学习,你都有哪些收获呢?
(1)概率的统计定义;
(2)概率与频率的区别与联系;
(3)求概率的方法;
(4)体会随机事件的随机性与稳定性(偶然与必然的辩证统一).
五、课下探究,拓展新知
探究1:站错队
在超市购物后结账,人多的时候,多数情况自己站的队伍慢,其它队伍快,总让人很是烦恼,你能利用所学的概率知识消除我的烦恼吗?
探究2:当你的指尖敲打着电脑键盘时,你是否想过,键盘上的字母为什么不按顺序排列?
我们不妨一起来做一次统计,先选取一篇英文文章,然后统计总的字母数,每个字母出现的频数与频率,你能发现什么?
北师大版《普通高中课程标准实验教科书》·数学·必修三
随机事件的概率
(第一课时)
一、创设情境,引入新知
生活实例:张梦雪里约奥运夺首金
一、创设情境,引入新知
生活实例2:女排逆转夺冠
一、创设情境,引入新知
思考一:
1、在张梦雪射击前,你能知道她会获得冠军吗?
2、在比赛前,你能猜到中国女排能夺得金牌吗?
一、创设情境,引入新知
思考二:
1、既然能否夺冠是随机事件,为什么派张梦雪参加奥运会,而不是派其他射击运动员参加?
2、张梦雪“击中靶心的可能性比其他射击运动员大”这一生活经验是如何得到的呢?
在生活中我们通常用射击试验命中的频率来估计命中的概率,那么这种方法是否具有普遍性?
(一)动手试验,探究随机事件的可能性大小
二、合作交流,探究新知
(1)试验目的:探究随机事件“抛掷一枚硬币,正面向上”的可能性大小.
(2)试验要求:
①假设硬币的材质是均匀的,所有的硬币都相同;
②从离桌面大约30cm的高度,让其自由下落在桌面上;
③5人一组,每人抛掷20次,共100次,各自认真记录 “正面向上”出现的次数,组长汇总本组的总次数.
认真阅读
二、合作交流,探究新知
(二)汇总数据,观察频率的特征
思考1:请仔细观察上表,频率呈现出什么样的特征?
特征1:每一组的频率不太一样,但频率基本上在一个常数0.5附近
摆动,个别偏离常数较大.
思考2:请同学们小组讨论频率偏离常数较大的原因.
原因:1.没有在相同条件下做试验;
2.由于随机事件的不确定性,当试验次数较少时,个别偏离
较大属于正常情况.
思考3:增加试验次数,继续观察频率有什么变化.
特征2:随着试验次数的增加,频率摆动的幅度有减小的趋势.
二、合作交流,探究新知
(三)观察分析,探究频率的规律性
特征2:随着试验次数的增加,频率摆动的幅度有减小的趋势,并
逐渐稳定于常数0.5.
二、合作交流,探究新知
(三)观察分析,探究频率的规律性
思考:
①能不能用某次试验的频率作为硬币正面向上的概率?
②用哪个量作为硬币正面向上的概率比较合适呢?
结论:在相同条件下,大量重复抛掷硬币时,出现正面向上的频率会在常数0.5附近摆动,随着试验次数的增加,正面向上的频率稳定于常数0.5 ,这个常数0.5就是正面向上的概率.
试验者 抛掷次数n 正面向上的次数m 频率m/n
德·摩根 2048 1061 0.5181
蒲丰 4040 2048 0.5069
费勒 10000 4979 0.4979
皮尔逊 24000 12012 0.5005
罗曼诺夫斯基 80640 40173 0.4982
二、合作交流,探究新知
(四)感知升华,概括结论
试验结论:在相同条件下,大量重复抛掷硬币试验时,出现正面向上的频率在常数0.5附近摆动,随着试验次数的增加,正面向上的频率稳定于常数0.5,这个常数0.5就是硬币正面向上的概率.
请同学们根据试验结论,尝试自己概括出概率的统计定义.
二、合作交流,探究新知
1.概率的统计定义
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率会在某一个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,我们把这个常数叫做随机事件A的概率,记作P(A).
(四)感知升华,概括结论
思考:随机事件A的概率 P(A)的取值范围是多少?随机事件的概率可以为0或1吗?你能举例说明吗?
二、合作交流,探究新知
1.概率的统计定义
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率会在某一个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,我们把这个常数叫做随机事件A的概率,记作P(A).
(四)感知升华,概括结论
范围:0≤P(A) ≤1.
如:大家都知道《守株待兔》这个成语故事,你会像故事中的农夫那样坐在树底下“待兔”吗?为什么?
大量重复试验
2.求随机事件概率的方法
二、合作交流,探究新知
3.“概率”和“频率”的区别与联系
(四)感知升华,概括结论
区别:频率反映了随机事件出现的频繁程度,是随机性
的;概率是确定的,是客观存在的,与试验无关.
联系:频率是概率的近似值,概率是频率的稳定值.
(1)在对一批种子进行的发芽试验中,抽取的10粒种子全部发芽,所以该种子的发芽率为100%;
(2)乒乓球比赛中,小李比小王获胜的概率大,若两人打一局比赛,小李一定获胜;
(3)因为抛掷一枚硬币出现正面的概率是0.5,所以抛掷12000次时,出现正面的次数很有可能接近6000次;
(4)某种彩票中奖的概率为 ,那么买1000张彩票一定能
中奖.
例1.判断下列说法的对错:
三、自主练习,应用新知
?
?
?
?
例2.某射手在同一条件下进行射击,结果如下:
0.90
0.93
0.88
0.92
0.89
0.91
(1)计算表中击中靶心的各个频率;
(2)这个射手射击一次,击中靶心的概率约为多少?
三、自主练习,应用新知
0.90
射击次数n 10 30 50 100 200 500
击中靶心的次数 m 9 28 44 92 178 455
击中靶心的频率m/n
四、课堂小结,再现新知
通过本节课的学习,你都有哪些收获呢?
(1)概率的统计定义;
(2)概率与频率的区别与联系;
(3)求概率的方法;
(4)体会随机事件的随机性与稳定性(偶然与必然的辩证统一).
五、课下探究,拓展新知
探究1:站错队
在超市购物后结账,人多的时候,多数情况自己站的队伍慢,其它队伍快,总让人很是烦恼,你能利用所学的概率知识消除我的烦恼吗?
探究2:当你的指尖敲打着电脑键盘时,你是否想过,键盘上的字母为什么不按顺序排列?
我们不妨一起来做一次统计,先选取一篇英文文章,然后统计总的字母数,每个字母出现的频数与频率,你能发现什么?
