人教A版数学选修2—2 1.1.2 导数的概念(共20张ppt)
文档属性
| 名称 | 人教A版数学选修2—2 1.1.2 导数的概念(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 418.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 11:44:17 | ||
图片预览







文档简介
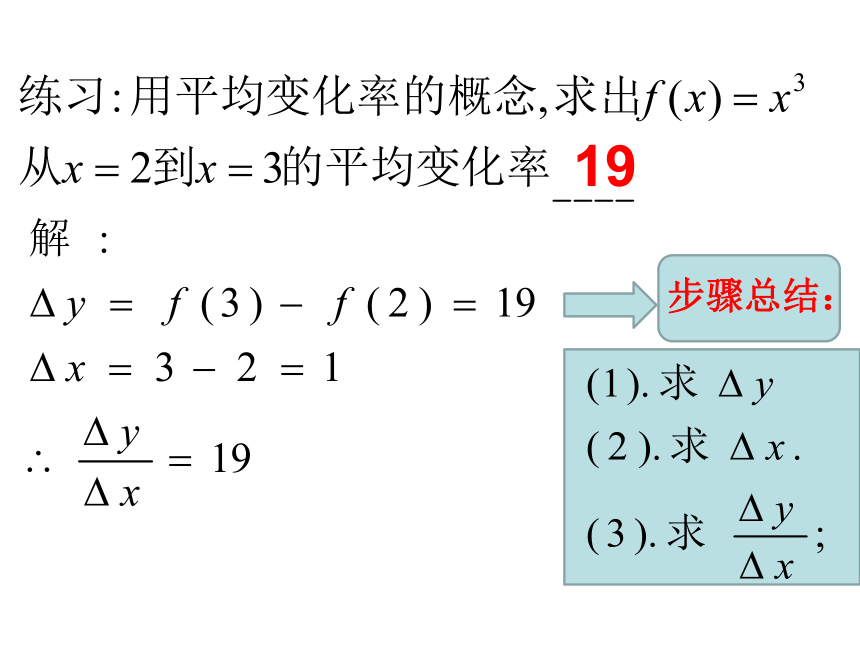
课件21张PPT。1.1.2 导数的概念旧知回顾 物理中:平均速度=数学中:平均变化率=19步骤总结:探究讨论:
高台跳水运动中,运动员相对于 水面的高度h(单位:m)与时间t(单位:s)问:
1.运动员在这段时间里是静止的吗?
2.用平均速度描述物体的运动状态有什么局限性?如何更为准确的刻画出物体在
某一时刻的运动状态呢?
瞬时速度学习目标:
1.知识目标:
理解导数的概念,初步掌握导数的计算方法,
并在具体数学问题中进一步理解导数的概念;
2.能力目标:
在导数概念建立的过程中,通过观察,数值逼近,
类比等方法体会数学概念的发生和形成;
3.德育目标:
从物理中的瞬时速度过渡到数学中的导数过程中,体会学科间的相互贯通,在探究实际生活的 例子中,
感受数学来源于生活,从而激发学生的学习热情;如何求运动员的瞬时速度呢?
比如,t=2时的瞬时速度是多少?求:从2s到(2+Δt)s这段时间内平均速度不妨先考察t=2附近的情况,
即在[ 2+△t, 2 ],[2, 2 +△t ]这段时间内的
平均速度当Δt趋近于0时,平均速度有什么变化趋势?当△t = 0.01时,当△t =0.001时, 当△t =0.0001时, 当△t = 0.00001, 当△t =0.000001,……当Δt趋近于0时,平均速度有什么变化趋势?当△t = 0.01时,当△t =0.001时,当△t =0.0001时,△t = 0.00001,△t =0.000001,……当Δt趋近于0时,平均速度有什么变化趋势?当△t = – 0.01时,当△t = 0.01时,当△t = – 0.001时,当△t =0.001时,当△t = –0.0001时,当△t =0.0001时,△t = – 0.00001,△t = 0.00001,△t = – 0.000001,△t =0.000001,………… 当Δt趋近于0时, 即无论 t 从小于2的一边, 还是从大于2的一边趋近于2时, 平均速度都趋近与一个确定的值 –13.1. 从物理的角度看, 时间间隔 |Δt |无限变小时, 平均速度 就无限趋近于 t = 2时的瞬时速度. 因此, 运动员在 t = 2 时的瞬时速度是 –13.1.表示“当t =2, Δt趋近于0时, 平均速度 趋近于确定值– 13.1”.=-13.1 从物理的角度看, 时间间隔 |Δt |无限变小时, 平均速度 就无限趋近于 t = 2时的瞬时速度. 因此, 运动员在 t = 2 时的瞬时速度是 –13.1.=-13.11.运动员在某一时刻 t0 的瞬时速度怎样表示?2.2.函数f (x)在 x = x0 处的瞬时变化率怎样表示?称为函数 y = f (x) 在 x = x0 处的导数,
记作或 ;例题1求函数y=x2在x=1处的导数.
将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为
f (x) = x2 – 7x+15 ( 0≤x≤8 ) .
计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.例2 例2 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为 f (x) = x2 – 7x+15 ( 0≤x≤8 ) . 计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.解: 在第2h和第6h时, 原油温度的瞬时变化率就是和根据导数的定义,所以,同理可得 在第2h和第6h时, 原油温度的瞬时变化率分别为–3和5. 它说明在第2h附近, 原油温度大约以3 / h的速率下降; 在第6h附近,原油温度大约以5 / h的速率上升.巩固练习:A.6 B.18 C.54 D.81B-3求函数y=f(x)在点x0处的导数的基本方法是:(1)求函数的增量(2)求平均变化率(3)求得导数归纳:物理中数学中物理中数学中平均速度平均变化率瞬时速度瞬时变化率(导数)拓展练习:变式:-3-12444
高台跳水运动中,运动员相对于 水面的高度h(单位:m)与时间t(单位:s)问:
1.运动员在这段时间里是静止的吗?
2.用平均速度描述物体的运动状态有什么局限性?如何更为准确的刻画出物体在
某一时刻的运动状态呢?
瞬时速度学习目标:
1.知识目标:
理解导数的概念,初步掌握导数的计算方法,
并在具体数学问题中进一步理解导数的概念;
2.能力目标:
在导数概念建立的过程中,通过观察,数值逼近,
类比等方法体会数学概念的发生和形成;
3.德育目标:
从物理中的瞬时速度过渡到数学中的导数过程中,体会学科间的相互贯通,在探究实际生活的 例子中,
感受数学来源于生活,从而激发学生的学习热情;如何求运动员的瞬时速度呢?
比如,t=2时的瞬时速度是多少?求:从2s到(2+Δt)s这段时间内平均速度不妨先考察t=2附近的情况,
即在[ 2+△t, 2 ],[2, 2 +△t ]这段时间内的
平均速度当Δt趋近于0时,平均速度有什么变化趋势?当△t = 0.01时,当△t =0.001时, 当△t =0.0001时, 当△t = 0.00001, 当△t =0.000001,……当Δt趋近于0时,平均速度有什么变化趋势?当△t = 0.01时,当△t =0.001时,当△t =0.0001时,△t = 0.00001,△t =0.000001,……当Δt趋近于0时,平均速度有什么变化趋势?当△t = – 0.01时,当△t = 0.01时,当△t = – 0.001时,当△t =0.001时,当△t = –0.0001时,当△t =0.0001时,△t = – 0.00001,△t = 0.00001,△t = – 0.000001,△t =0.000001,………… 当Δt趋近于0时, 即无论 t 从小于2的一边, 还是从大于2的一边趋近于2时, 平均速度都趋近与一个确定的值 –13.1. 从物理的角度看, 时间间隔 |Δt |无限变小时, 平均速度 就无限趋近于 t = 2时的瞬时速度. 因此, 运动员在 t = 2 时的瞬时速度是 –13.1.表示“当t =2, Δt趋近于0时, 平均速度 趋近于确定值– 13.1”.=-13.1 从物理的角度看, 时间间隔 |Δt |无限变小时, 平均速度 就无限趋近于 t = 2时的瞬时速度. 因此, 运动员在 t = 2 时的瞬时速度是 –13.1.=-13.11.运动员在某一时刻 t0 的瞬时速度怎样表示?2.2.函数f (x)在 x = x0 处的瞬时变化率怎样表示?称为函数 y = f (x) 在 x = x0 处的导数,
记作或 ;例题1求函数y=x2在x=1处的导数.
将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为
f (x) = x2 – 7x+15 ( 0≤x≤8 ) .
计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.例2 例2 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为 f (x) = x2 – 7x+15 ( 0≤x≤8 ) . 计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.解: 在第2h和第6h时, 原油温度的瞬时变化率就是和根据导数的定义,所以,同理可得 在第2h和第6h时, 原油温度的瞬时变化率分别为–3和5. 它说明在第2h附近, 原油温度大约以3 / h的速率下降; 在第6h附近,原油温度大约以5 / h的速率上升.巩固练习:A.6 B.18 C.54 D.81B-3求函数y=f(x)在点x0处的导数的基本方法是:(1)求函数的增量(2)求平均变化率(3)求得导数归纳:物理中数学中物理中数学中平均速度平均变化率瞬时速度瞬时变化率(导数)拓展练习:变式:-3-12444
