人教A版数学选修2—2 1.3.1 函数的单调性与导数(共15张ppt)
文档属性
| 名称 | 人教A版数学选修2—2 1.3.1 函数的单调性与导数(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 184.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 11:53:06 | ||
图片预览




文档简介
课件15张PPT。一、新课导入------温故知新问题1. 函数的导数是怎样定义的? 它是刻画函数
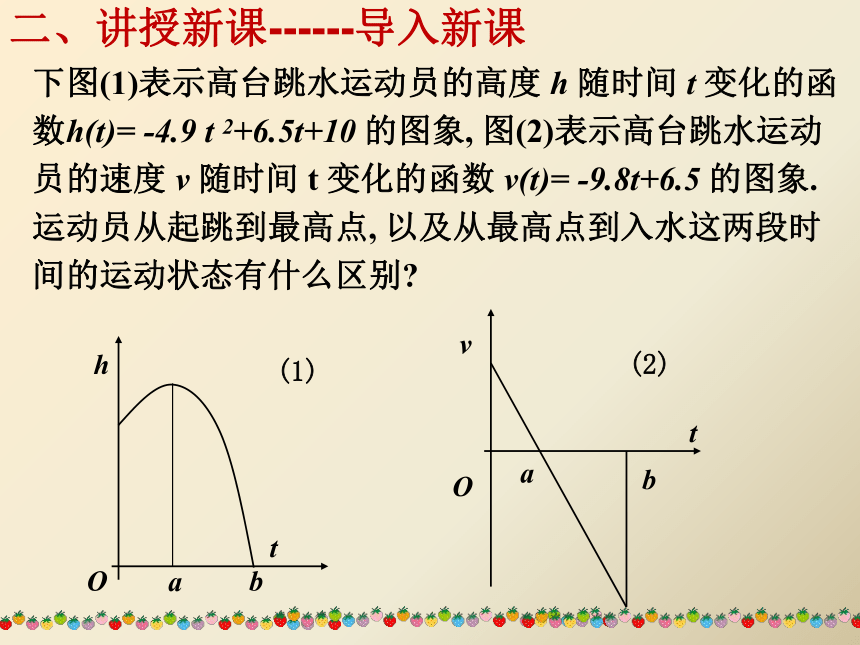
的什么特征的?问题2. 函数的单调性是如何体现函数值的变化的? 问题3. 函数的单调性与导数之间有什么联系? 1.3.1函数的单调性与导数 下图(1)表示高台跳水运动员的高度 h 随时间 t 变化的函数h(t)= -4.9 t 2+6.5t+10 的图象, 图(2)表示高台跳水运动员的速度 v 随时间 t 变化的函数 v(t)= -9.8t+6.5 的图象.运动员从起跳到最高点, 以及从最高点到入水这两段时间的运动状态有什么区别?hOabt(1)Ovt(2)ab二、讲授新课------导入新课①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地,v(t)=h'(t)>0.②从最高点到入水,运动员离水面的高度h随时间t的增加而减少,即h(t)是减函数.相应地,v(t)=h'(t)<0.
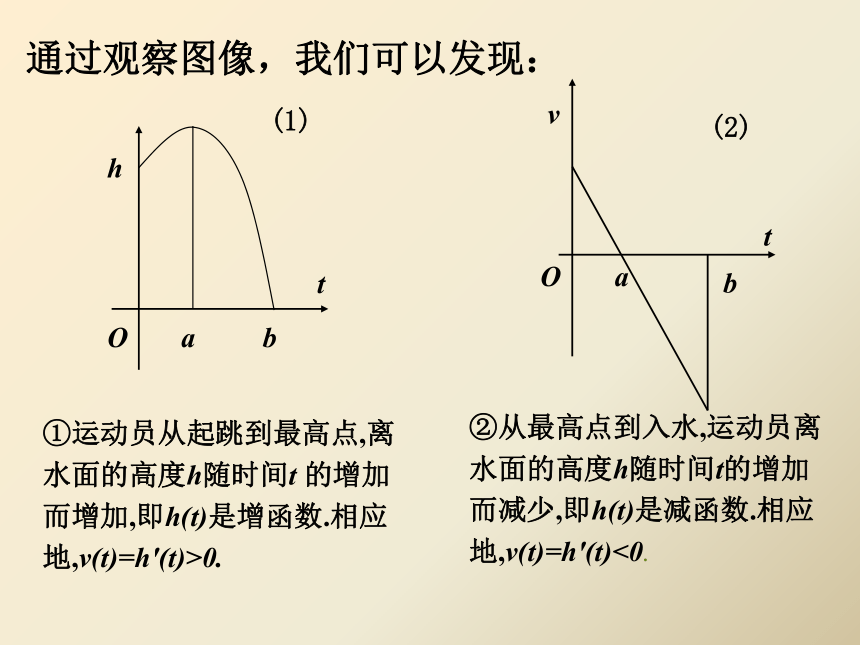
O(1)abhtOvtab(2)通过观察图像,我们可以发现: 观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系.二、讲授新课-----问题探究yxy=xoyxo(2)(1)y=x2xyo(3)y=x3(4)xyo二、讲授新课-----问题探究yxoy=f(x) 一般地,函数的单调性与其导函数的正负有如下关系:
在某个区间(a,b)内,
如果 f '(x) >0 , 那么函数y=f(x)在这个区间内单调递增;
如果 f '(x)<0 , 那么函数y=f(x)在这个区间内单调递减;
(x0,f(x0))(x1,f(x1))二、讲授新课-----问题探究如果 在某个区间内恒有f '(x)=0 , 那么函数y=f(x)在这个区间内是常数函数.问题4. 如果 在某个区间内恒有f ‘(x)=0 , 那么函数 y=f(x)的图像有什么特征呢.例 1. 已知导函数 f '(x) 的下列信息:当1 < x < 4 时, f '(x)>0;当 x > 4 , 或 x < 1时, f '(x) <0;
当 x = 4 , 或 x = 1时, f '(x) =0。试画出函数 f (x) 的图象的大致形状.解: 当1 < x < 4 时, f '(x) >0,可知 f (x) 在此区间内单调递增;当 x > 4 , 或 x < 1时, f '(x) <0 ,可知 f (x) 在此区间内单调递减;当 x = 4 , 或 x = 1时, f '(x) =0 . (这两点比较特殊,我们称他们为“临界点”) 综上, 函数 f (x) 图象的大致形状如右图所示.二、讲授新课-----牛刀小试二、讲授新课-----牛刀小试练习. 设导函数y=f '(x)的图象如图,则其原函数可能为( )(A)(B)(C)(D)Cy=f(x)y=f(x)y=f(x)y=f(x)二、讲授新课-----典例精讲例 2. 判断下列函数的单调性, 并求出单调区间:f(x)=x2-2x-3
f(x)=x3+3x
(3) f(x)=x2-2lnx例 2. 判断下列函数的单调性, 并求出单调区间:二、讲授新课-----典例精讲解:(2) f(x)=x3+3x
(3) f(x)=x2-2lnx(2)f '(x)=x3+3x= 3(x2+1)>0 所以函数f(x)=x3+3x在R上单调递增。
所以函数f(x)=x3+3x的单调增区间为R。
二、讲授新课-----典例精讲例 3. 判断下列函数的单调性, 并求出单调区间:(3) f(x)=x2-2lnx解:当f '(x)>0,即x>1时,函数f(x)=x2-2lnx单调递增;当f '(x)<0,即00和f '(x)<0;(4)根据(3)的结果确认f(x)的单调区间。四、巩固练习f '(x)=3x-x3=3-3x2=-3(x2-1)=-3(x-1)(x+1)
当f '(x)>0,即-11或x<-1时,函数f(x)=3x-x3 单调递减;判断下列函数的单调性, 并求出单调区间:
(1) (2)f(x)=sinx-x 0解:f(x)=3x-x3五、课堂小结在某个区间(a,b)内,
如果 f '(x) >0 ,那么函数在这个区间内单调递增;
如果 f '(x)<0 , 那么函数在这个区间内单调递减;
2.利用导函数求函数f(x)的单调区间的一般步骤为:(1)确定函数f(x)的定义域;
(2)求导数f '(x);
(3)在函数f(x)的定义域内解不等式f '(x)>0和f '(x)<0;
(4)根据(3)的结果确认f(x)的单调区间。1.函数的单调性与导函数的正负的关系:
的什么特征的?问题2. 函数的单调性是如何体现函数值的变化的? 问题3. 函数的单调性与导数之间有什么联系? 1.3.1函数的单调性与导数 下图(1)表示高台跳水运动员的高度 h 随时间 t 变化的函数h(t)= -4.9 t 2+6.5t+10 的图象, 图(2)表示高台跳水运动员的速度 v 随时间 t 变化的函数 v(t)= -9.8t+6.5 的图象.运动员从起跳到最高点, 以及从最高点到入水这两段时间的运动状态有什么区别?hOabt(1)Ovt(2)ab二、讲授新课------导入新课①运动员从起跳到最高点,离水面的高度h随时间t 的增加而增加,即h(t)是增函数.相应地,v(t)=h'(t)>0.②从最高点到入水,运动员离水面的高度h随时间t的增加而减少,即h(t)是减函数.相应地,v(t)=h'(t)<0.
O(1)abhtOvtab(2)通过观察图像,我们可以发现: 观察下面一些函数的图象, 探讨函数的单调性与其导函数正负的关系.二、讲授新课-----问题探究yxy=xoyxo(2)(1)y=x2xyo(3)y=x3(4)xyo二、讲授新课-----问题探究yxoy=f(x) 一般地,函数的单调性与其导函数的正负有如下关系:
在某个区间(a,b)内,
如果 f '(x) >0 , 那么函数y=f(x)在这个区间内单调递增;
如果 f '(x)<0 , 那么函数y=f(x)在这个区间内单调递减;
(x0,f(x0))(x1,f(x1))二、讲授新课-----问题探究如果 在某个区间内恒有f '(x)=0 , 那么函数y=f(x)在这个区间内是常数函数.问题4. 如果 在某个区间内恒有f ‘(x)=0 , 那么函数 y=f(x)的图像有什么特征呢.例 1. 已知导函数 f '(x) 的下列信息:当1 < x < 4 时, f '(x)>0;当 x > 4 , 或 x < 1时, f '(x) <0;
当 x = 4 , 或 x = 1时, f '(x) =0。试画出函数 f (x) 的图象的大致形状.解: 当1 < x < 4 时, f '(x) >0,可知 f (x) 在此区间内单调递增;当 x > 4 , 或 x < 1时, f '(x) <0 ,可知 f (x) 在此区间内单调递减;当 x = 4 , 或 x = 1时, f '(x) =0 . (这两点比较特殊,我们称他们为“临界点”) 综上, 函数 f (x) 图象的大致形状如右图所示.二、讲授新课-----牛刀小试二、讲授新课-----牛刀小试练习. 设导函数y=f '(x)的图象如图,则其原函数可能为( )(A)(B)(C)(D)Cy=f(x)y=f(x)y=f(x)y=f(x)二、讲授新课-----典例精讲例 2. 判断下列函数的单调性, 并求出单调区间:f(x)=x2-2x-3
f(x)=x3+3x
(3) f(x)=x2-2lnx例 2. 判断下列函数的单调性, 并求出单调区间:二、讲授新课-----典例精讲解:(2) f(x)=x3+3x
(3) f(x)=x2-2lnx(2)f '(x)=x3+3x= 3(x2+1)>0 所以函数f(x)=x3+3x在R上单调递增。
所以函数f(x)=x3+3x的单调增区间为R。
二、讲授新课-----典例精讲例 3. 判断下列函数的单调性, 并求出单调区间:(3) f(x)=x2-2lnx解:当f '(x)>0,即x>1时,函数f(x)=x2-2lnx单调递增;当f '(x)<0,即0
当f '(x)>0,即-1
(1) (2)f(x)=sinx-x 0
如果 f '(x) >0 ,那么函数在这个区间内单调递增;
如果 f '(x)<0 , 那么函数在这个区间内单调递减;
2.利用导函数求函数f(x)的单调区间的一般步骤为:(1)确定函数f(x)的定义域;
(2)求导数f '(x);
(3)在函数f(x)的定义域内解不等式f '(x)>0和f '(x)<0;
(4)根据(3)的结果确认f(x)的单调区间。1.函数的单调性与导函数的正负的关系:
