人教版A版选修4—4 1.1 平面直角坐标系(共22张ppt)
文档属性
| 名称 | 人教版A版选修4—4 1.1 平面直角坐标系(共22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 526.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 11:53:32 | ||
图片预览




文档简介
课件22张PPT。【学习目标】1.回顾在平面直角坐标系中刻画点的位置的方法,体会坐标系的作用并领会坐标法的应用.
2.了解在伸缩变换作用下平面图形的变化情况,掌握平面直角坐标系中的伸缩变换.(重点、难点)
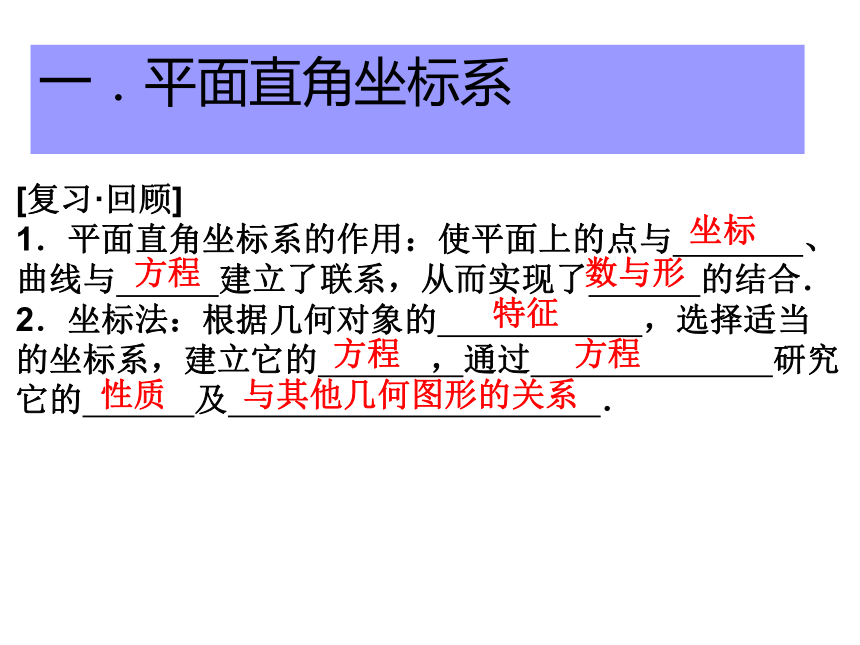
3.能够建立适当的直角坐标系,运用坐标法解决数学问题.坐标方程数与形特征方程方程性质与其他几何图形的关系一.平面直角坐标系[复习·回顾]
1.平面直角坐标系的作用:使平面上的点与 、 曲线与 建立了联系,从而实现了 的结合.
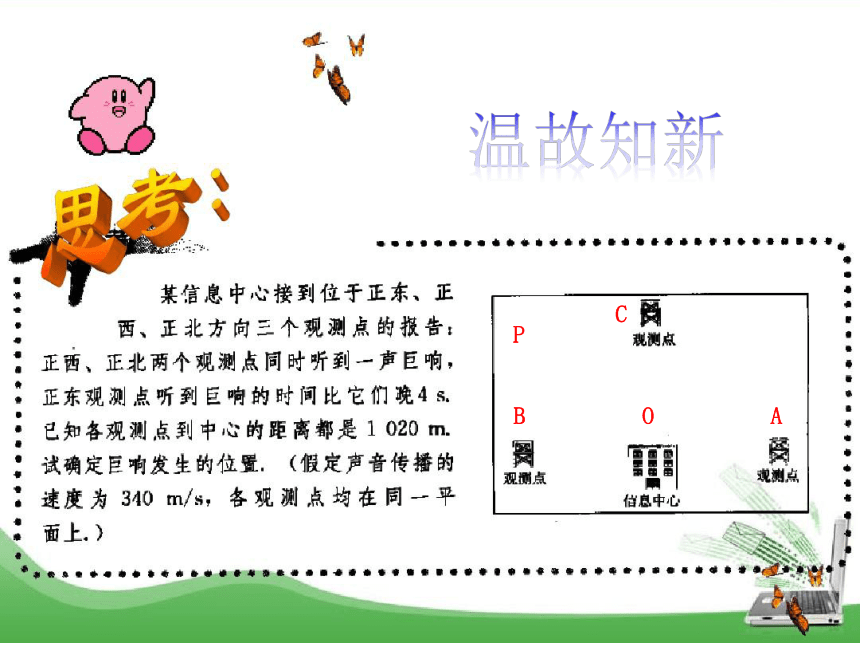
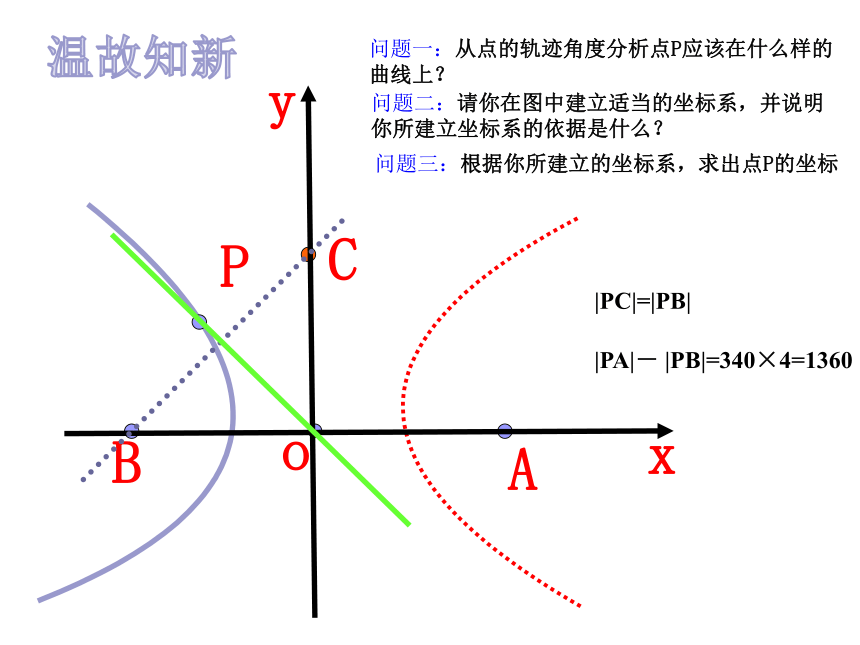
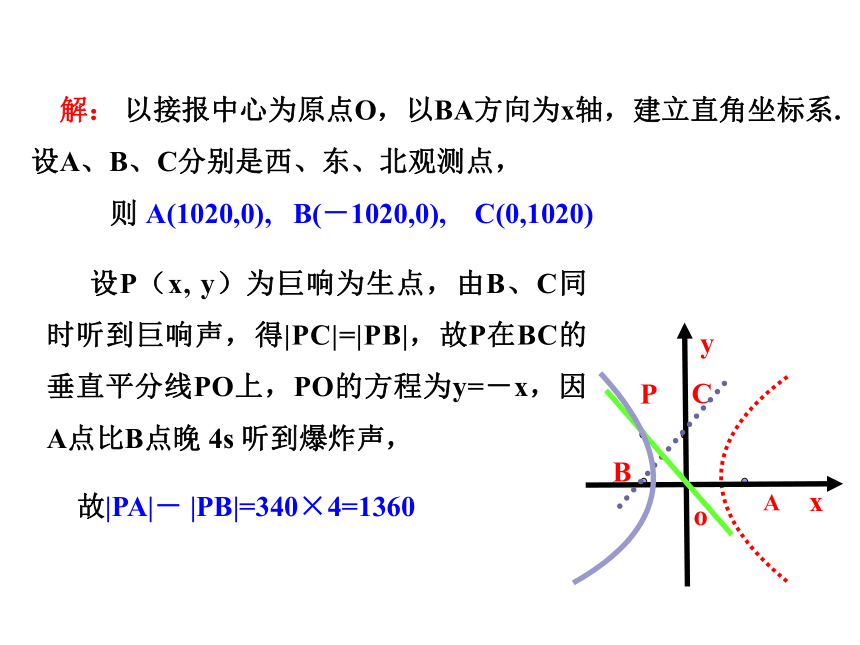
2.坐标法:根据几何对象的 ,选择适当的坐标系,建立它的 ,通过 研究它的 及 .温故知新ABCOPyxBACPo问题一:从点的轨迹角度分析点P应该在什么样的曲线上?问题二:请你在图中建立适当的坐标系,并说明你所建立坐标系的依据是什么? 问题三:根据你所建立的坐标系,求出点P的坐标温故知新|PC|=|PB||PA|- |PB|=340×4=1360 解: 以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点, 设P(x, y)为巨响为生点,由B、C同时听到巨响声,得|PC|=|PB|,故P在BC的垂直平分线PO上,PO的方程为y=-x,因A点比B点晚 4s 听到爆炸声,yxBACPo则 A(1020,0), B(-1020,0), C(0,1020)故|PA|- |PB|=340×4=1360
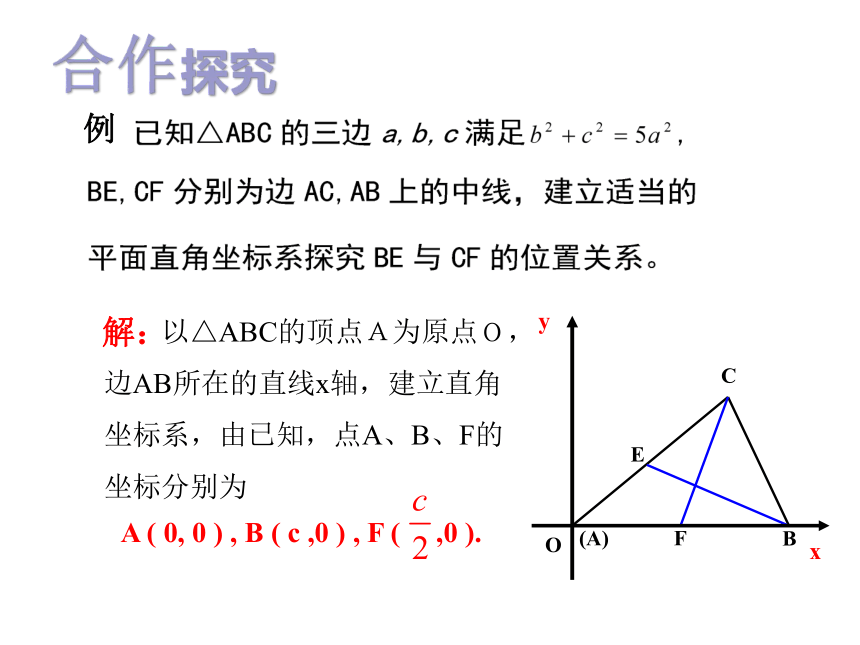
坐标法解决平面几何问题的“三步曲”:回顾总结坐标法解决平面几何问题的一般步骤第二步,通过代数运算,解决代数问题;第三步,把代数运算结果翻译成几何结论。第一步,建立适当坐标系,用坐标和方程表示问 题中涉及的几何元素,将平面几何问题转化成代 数问题;yx 以△ABC的顶点A为原点O,
边AB所在的直线x轴,建立直角
坐标系,由已知,点A、B、F的
坐标分别为解:例合作探究因此,BE与CF互相垂直.yx比较不同的直角坐标系下解决问题的过程,建立直角坐标系应注意哪些问题?【规律总结】建立平面直角坐标系时,要根据图形的几何特点选择适当的直角坐标系。(1)如果图形有对称中心,可以选对称中心为坐标原点;(2)如果图形有对称轴,可以选择对称轴为坐标轴;(3)使图形上的特殊点尽可能多的在坐标轴上。建立适当直角坐标系的一般规则:二、平面直角坐标系中的伸缩变换怎样由正弦曲线y=sinx得到曲线y=sin2x? 在正弦曲线y=sinx上任取一点P(x, y),保持纵坐标y不变,将横坐标x缩为原来的1/2,那么正弦曲线y=sinx就变成曲线y=sin2x。上述变换实质上就是一个坐标的压缩变换即:设P(x,y)是平面直角坐标系中任意一点, 保持纵坐标y不变,将横坐标x缩为原来1/2,得到点P′(x′,y′),坐标对应关系为:我们把①式叫做平面直角坐标系中的一个坐标压缩变换。y=sin2xy=sinx探求新知怎样由正弦曲线y=sinx得到曲线y=3sinx?在正弦曲线上任取一点P(x, y),保持横坐标x不变,将纵坐标伸长为原来的3倍,就得到曲线y=3sinx。上述变换实质上就是一个坐标的伸长变换即:设P(x,y)是平面直角坐标系中任意一点,保持横坐标x不变,将纵坐标y伸长为原来的3倍,得到点P′ (x′,y′),坐标对应关系为:我们把②式叫做平面直角坐标系中的一个坐标伸长变换.探求新知 在正弦曲线y=sinx上任取一点P(x, y),先保持纵坐标y不变将横坐标x缩为原来的1/2;在此基础上,再将纵坐标变为原来的3倍,就得到曲线y=3sin2x.
怎样由正弦曲线y=sinx得到曲线y=3sin2x?
设P(x,y)是平面直角坐标系中的任意一点,经过上述变换后变为点P′(x′,y′),那么坐标对应关系为:我们把③式叫做平直角坐标系中的一个坐标伸缩变换.实际上,这是上述①②的“合成”探求新知设点P(x, y)是平面直角坐标系中任意一点,在变换:定义:的作用下,点P(x, y) 对应点P′(x′,y′), 上述①②③都是坐标伸缩变换,在它们的作用下,可以实现平面图形的伸缩。③在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。②把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;获取新知①λ>0,μ>0;注意:例1 在直角坐标系中,求下列方程所对应的图形经过伸缩变换: 后的图形。
(1) 2x+3y=0;(2) x2+y2=1代入2x+3y=0;; 已知伸缩变换及原曲线方程,求变换后曲线方程代入法因此,经过此伸缩变换后,直线2x+3y=0变成直线经过此伸缩变换后圆变成椭圆典例欣赏在同一直角坐标系中,经过伸缩变换
后,曲线C变为曲线 ,求曲线C的方程。已知伸缩变换及变换后曲线方程,可求原曲线方程练习1学以致用,应用新知在同一平面直角坐标系中,求满足下列图形变换的伸缩变换:曲线变成曲线思路点拨:设出伸缩变换公式,由条件列出λ、μ的方程,解方程求出λ、μ的值即可,注意λ>0,μ>0 。练习2比较方程可得由此可得伸缩变换
A2.将直线x+y=1变换为直线2x′+3y′=6的一个伸缩变换为( )
A. B.
C. D.
A随堂检测,巩固提高1.在平面直角坐标系中,坐标法研究平面几何问题的一般步骤,根据几何特点建立适当直角坐标系的一般规则;2.平面直角坐标系中的坐标伸缩变换;3.应用坐标法、代入法和方程思想解决平面图形的伸缩变换问题。课堂小结课后思考:
在伸缩变换下,椭圆是否可以变成圆?抛物线、双曲线变成什么曲线?
2.了解在伸缩变换作用下平面图形的变化情况,掌握平面直角坐标系中的伸缩变换.(重点、难点)
3.能够建立适当的直角坐标系,运用坐标法解决数学问题.坐标方程数与形特征方程方程性质与其他几何图形的关系一.平面直角坐标系[复习·回顾]
1.平面直角坐标系的作用:使平面上的点与 、 曲线与 建立了联系,从而实现了 的结合.
2.坐标法:根据几何对象的 ,选择适当的坐标系,建立它的 ,通过 研究它的 及 .温故知新ABCOPyxBACPo问题一:从点的轨迹角度分析点P应该在什么样的曲线上?问题二:请你在图中建立适当的坐标系,并说明你所建立坐标系的依据是什么? 问题三:根据你所建立的坐标系,求出点P的坐标温故知新|PC|=|PB||PA|- |PB|=340×4=1360 解: 以接报中心为原点O,以BA方向为x轴,建立直角坐标系.设A、B、C分别是西、东、北观测点, 设P(x, y)为巨响为生点,由B、C同时听到巨响声,得|PC|=|PB|,故P在BC的垂直平分线PO上,PO的方程为y=-x,因A点比B点晚 4s 听到爆炸声,yxBACPo则 A(1020,0), B(-1020,0), C(0,1020)故|PA|- |PB|=340×4=1360
坐标法解决平面几何问题的“三步曲”:回顾总结坐标法解决平面几何问题的一般步骤第二步,通过代数运算,解决代数问题;第三步,把代数运算结果翻译成几何结论。第一步,建立适当坐标系,用坐标和方程表示问 题中涉及的几何元素,将平面几何问题转化成代 数问题;yx 以△ABC的顶点A为原点O,
边AB所在的直线x轴,建立直角
坐标系,由已知,点A、B、F的
坐标分别为解:例合作探究因此,BE与CF互相垂直.yx比较不同的直角坐标系下解决问题的过程,建立直角坐标系应注意哪些问题?【规律总结】建立平面直角坐标系时,要根据图形的几何特点选择适当的直角坐标系。(1)如果图形有对称中心,可以选对称中心为坐标原点;(2)如果图形有对称轴,可以选择对称轴为坐标轴;(3)使图形上的特殊点尽可能多的在坐标轴上。建立适当直角坐标系的一般规则:二、平面直角坐标系中的伸缩变换怎样由正弦曲线y=sinx得到曲线y=sin2x? 在正弦曲线y=sinx上任取一点P(x, y),保持纵坐标y不变,将横坐标x缩为原来的1/2,那么正弦曲线y=sinx就变成曲线y=sin2x。上述变换实质上就是一个坐标的压缩变换即:设P(x,y)是平面直角坐标系中任意一点, 保持纵坐标y不变,将横坐标x缩为原来1/2,得到点P′(x′,y′),坐标对应关系为:我们把①式叫做平面直角坐标系中的一个坐标压缩变换。y=sin2xy=sinx探求新知怎样由正弦曲线y=sinx得到曲线y=3sinx?在正弦曲线上任取一点P(x, y),保持横坐标x不变,将纵坐标伸长为原来的3倍,就得到曲线y=3sinx。上述变换实质上就是一个坐标的伸长变换即:设P(x,y)是平面直角坐标系中任意一点,保持横坐标x不变,将纵坐标y伸长为原来的3倍,得到点P′ (x′,y′),坐标对应关系为:我们把②式叫做平面直角坐标系中的一个坐标伸长变换.探求新知 在正弦曲线y=sinx上任取一点P(x, y),先保持纵坐标y不变将横坐标x缩为原来的1/2;在此基础上,再将纵坐标变为原来的3倍,就得到曲线y=3sin2x.
怎样由正弦曲线y=sinx得到曲线y=3sin2x?
设P(x,y)是平面直角坐标系中的任意一点,经过上述变换后变为点P′(x′,y′),那么坐标对应关系为:我们把③式叫做平直角坐标系中的一个坐标伸缩变换.实际上,这是上述①②的“合成”探求新知设点P(x, y)是平面直角坐标系中任意一点,在变换:定义:的作用下,点P(x, y) 对应点P′(x′,y′), 上述①②③都是坐标伸缩变换,在它们的作用下,可以实现平面图形的伸缩。③在伸缩变换下,平面直角坐标系不变,在同一直角坐标系下进行伸缩变换。②把图形看成点的运动轨迹,平面图形的伸缩变换可以用坐标伸缩变换得到;获取新知①λ>0,μ>0;注意:例1 在直角坐标系中,求下列方程所对应的图形经过伸缩变换: 后的图形。
(1) 2x+3y=0;(2) x2+y2=1代入2x+3y=0;; 已知伸缩变换及原曲线方程,求变换后曲线方程代入法因此,经过此伸缩变换后,直线2x+3y=0变成直线经过此伸缩变换后圆变成椭圆典例欣赏在同一直角坐标系中,经过伸缩变换
后,曲线C变为曲线 ,求曲线C的方程。已知伸缩变换及变换后曲线方程,可求原曲线方程练习1学以致用,应用新知在同一平面直角坐标系中,求满足下列图形变换的伸缩变换:曲线变成曲线思路点拨:设出伸缩变换公式,由条件列出λ、μ的方程,解方程求出λ、μ的值即可,注意λ>0,μ>0 。练习2比较方程可得由此可得伸缩变换
A2.将直线x+y=1变换为直线2x′+3y′=6的一个伸缩变换为( )
A. B.
C. D.
A随堂检测,巩固提高1.在平面直角坐标系中,坐标法研究平面几何问题的一般步骤,根据几何特点建立适当直角坐标系的一般规则;2.平面直角坐标系中的坐标伸缩变换;3.应用坐标法、代入法和方程思想解决平面图形的伸缩变换问题。课堂小结课后思考:
在伸缩变换下,椭圆是否可以变成圆?抛物线、双曲线变成什么曲线?
