人教版A版选修4—4 第一讲 极坐标系(共20张ppt)
文档属性
| 名称 | 人教版A版选修4—4 第一讲 极坐标系(共20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 00:00:00 | ||
图片预览






文档简介
课件20张PPT。 选修4-4
第一讲 极坐标系1.理解极坐标系及其概念,会求点的极坐标
2.能建立极坐标系,由点的极坐标确定位置
3.掌握点的极坐标与直角坐标的互化公式教学目标: 你好 请问:去第六
中学怎么走?从这向北偏西
走 米。情景感知问路人好心人这句话中,哪些地方是需要我们从数学角度去关注的?从 这 向 北偏西 走 米!方向距离这种用方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。情景分析出发点60°60m45°C图书馆D实验楼50m120mB体育馆A教学楼办公楼E右图为某校园的平面示意图。
假设某同学在教学楼处,
请回答下列问题:
(1)他向东偏北60 °方向
走120m后到达什么位置?
(2)如果有人打听体育馆
和办公楼的位置,他应
如何描述?
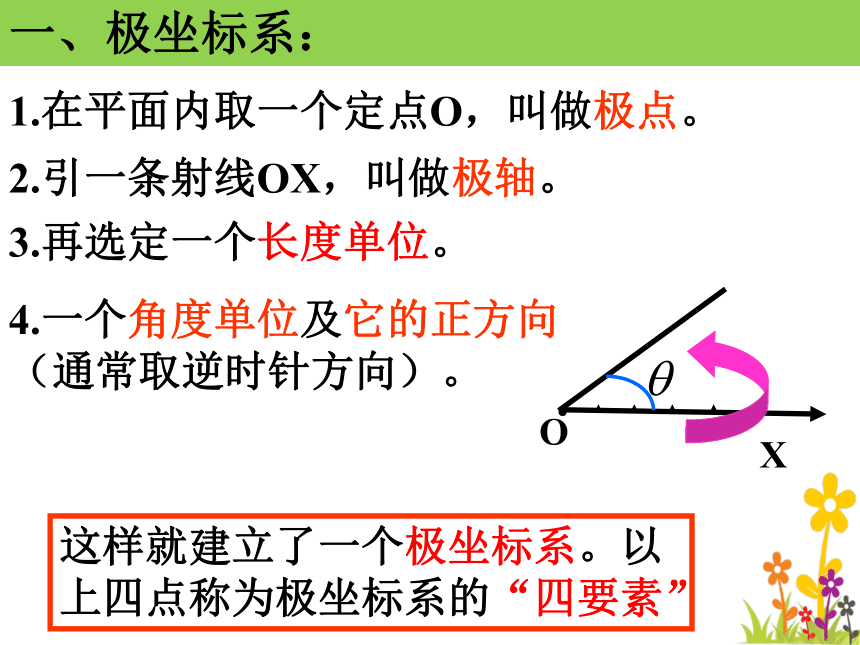
思考一:请大家类比直角坐标系的建立过程,试着建立一个用距离与角度确定平面上一点位置的坐标系.我来试一试:一、极坐标系:1.在平面内取一个定点O,叫做极点。2.引一条射线OX,叫做极轴。3.再选定一个长度单位。
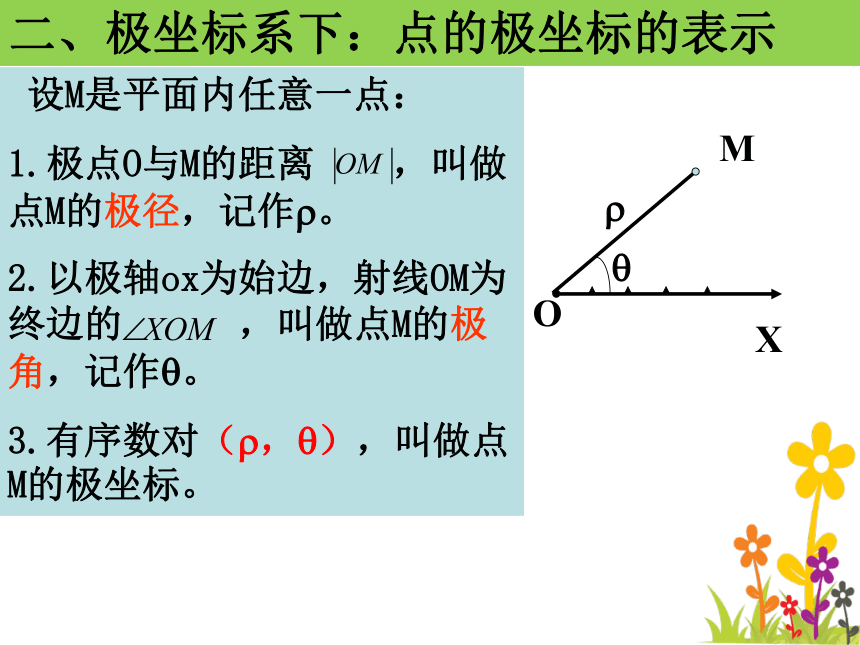
4.一个角度单位及它的正方向(通常取逆时针方向)。这样就建立了一个极坐标系。以上四点称为极坐标系的“四要素”O二、极坐标系下:点的极坐标的表示 设M是平面内任意一点:
1.极点O与M的距离 ,叫做点M的极径,记作?。
2.以极轴ox为始边,射线OM为终边的 ,叫做点M的极角,记作?。
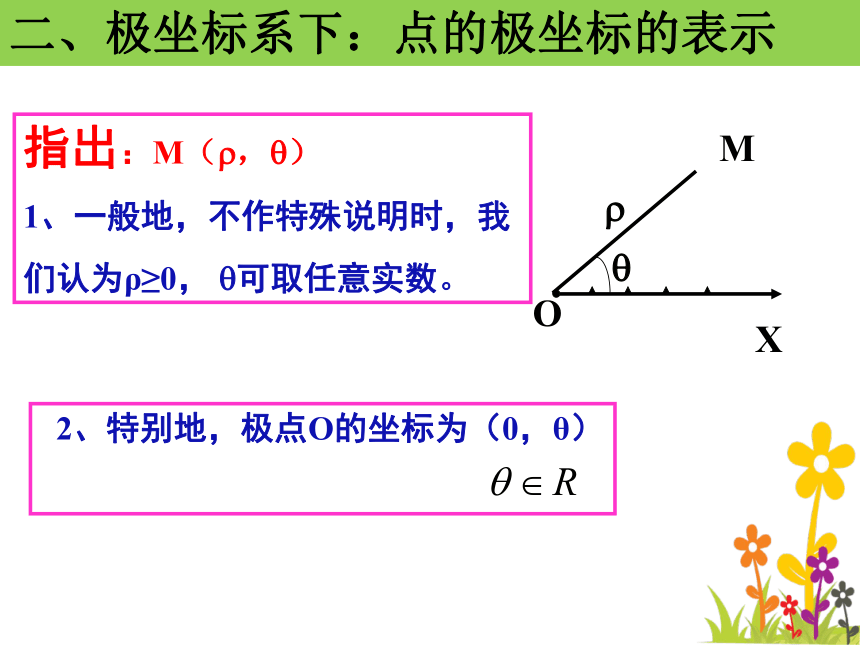
3.有序数对(?,?),叫做点M的极坐标。二、极坐标系下:点的极坐标的表示指出:M(?,?)
1、一般地,不作特殊说明时,我
们认为ρ≥0, ?可取任意实数。 2、特别地,极点O的坐标为(0,θ)
例1、 如图,1)写出各点的极坐标:A(4,0)C?小试牛刀?例2:下图是某校园的平面示意图,点
A,B,C,D,E分别表示教学楼,体育馆,图书馆,实验楼,办公楼的位置,建立适当的极坐标系,写出各点的极坐标。情景例题再现①平面上一点的极坐标是否唯一?
②若不唯一,那有多少种表示方法?
③坐标不唯一是由谁引起的?思考二:同位交流再思考:极坐标系下,点与它的极坐标的关系1.定点(?,?),可以在极坐标
系下确定唯一的点M。 2.给定平面上一点M,会有无
数个极坐标与之对应。原因在于:极角有无数个。3.如果限定ρ>0,0≤θ<2π那么,平面内的点和极坐标就可以一一对应.
(极点除外)小结:课堂跟踪练习 (小擂台)1.已知极坐标 ,下列所给出的
不能表示点M的坐标的是( )CD2.在极坐标系中,与(ρ,θ)关于极轴
对称的点是( )A.(ρ,3 π -θ) B.(ρ, π -θ)
C.(ρ,θ+π) D.(ρ,-θ)小组合作探究平面内的一个点既可以用直角坐标表示,也可以用极坐标表示,那么这两种坐标之间有什么关系?温馨提示:
1.把直角坐标系的原点作为极点
2.X轴的正半轴作为极轴
3.两种坐标系中取相同的长度单位
4.M的直角坐标(x,y),极坐标( ρ,θ )y(x,y)三、极坐标与直角坐标的互化公式点M的直角坐标(x,y)极坐标( ρ,θ )例题赏析温馨提示:挑战自己:(当堂巩固提升)课堂小结:本节课我们主要学习了:课后实践作业问题1:极坐标下点M的坐标( ρ,θ )
求:点M关于极点,极轴的对称点?
第一讲 极坐标系1.理解极坐标系及其概念,会求点的极坐标
2.能建立极坐标系,由点的极坐标确定位置
3.掌握点的极坐标与直角坐标的互化公式教学目标: 你好 请问:去第六
中学怎么走?从这向北偏西
走 米。情景感知问路人好心人这句话中,哪些地方是需要我们从数学角度去关注的?从 这 向 北偏西 走 米!方向距离这种用方向和距离表示平面上一点的位置的思想,就是极坐标的基本思想。情景分析出发点60°60m45°C图书馆D实验楼50m120mB体育馆A教学楼办公楼E右图为某校园的平面示意图。
假设某同学在教学楼处,
请回答下列问题:
(1)他向东偏北60 °方向
走120m后到达什么位置?
(2)如果有人打听体育馆
和办公楼的位置,他应
如何描述?
思考一:请大家类比直角坐标系的建立过程,试着建立一个用距离与角度确定平面上一点位置的坐标系.我来试一试:一、极坐标系:1.在平面内取一个定点O,叫做极点。2.引一条射线OX,叫做极轴。3.再选定一个长度单位。
4.一个角度单位及它的正方向(通常取逆时针方向)。这样就建立了一个极坐标系。以上四点称为极坐标系的“四要素”O二、极坐标系下:点的极坐标的表示 设M是平面内任意一点:
1.极点O与M的距离 ,叫做点M的极径,记作?。
2.以极轴ox为始边,射线OM为终边的 ,叫做点M的极角,记作?。
3.有序数对(?,?),叫做点M的极坐标。二、极坐标系下:点的极坐标的表示指出:M(?,?)
1、一般地,不作特殊说明时,我
们认为ρ≥0, ?可取任意实数。 2、特别地,极点O的坐标为(0,θ)
例1、 如图,1)写出各点的极坐标:A(4,0)C?小试牛刀?例2:下图是某校园的平面示意图,点
A,B,C,D,E分别表示教学楼,体育馆,图书馆,实验楼,办公楼的位置,建立适当的极坐标系,写出各点的极坐标。情景例题再现①平面上一点的极坐标是否唯一?
②若不唯一,那有多少种表示方法?
③坐标不唯一是由谁引起的?思考二:同位交流再思考:极坐标系下,点与它的极坐标的关系1.定点(?,?),可以在极坐标
系下确定唯一的点M。 2.给定平面上一点M,会有无
数个极坐标与之对应。原因在于:极角有无数个。3.如果限定ρ>0,0≤θ<2π那么,平面内的点和极坐标就可以一一对应.
(极点除外)小结:课堂跟踪练习 (小擂台)1.已知极坐标 ,下列所给出的
不能表示点M的坐标的是( )CD2.在极坐标系中,与(ρ,θ)关于极轴
对称的点是( )A.(ρ,3 π -θ) B.(ρ, π -θ)
C.(ρ,θ+π) D.(ρ,-θ)小组合作探究平面内的一个点既可以用直角坐标表示,也可以用极坐标表示,那么这两种坐标之间有什么关系?温馨提示:
1.把直角坐标系的原点作为极点
2.X轴的正半轴作为极轴
3.两种坐标系中取相同的长度单位
4.M的直角坐标(x,y),极坐标( ρ,θ )y(x,y)三、极坐标与直角坐标的互化公式点M的直角坐标(x,y)极坐标( ρ,θ )例题赏析温馨提示:挑战自己:(当堂巩固提升)课堂小结:本节课我们主要学习了:课后实践作业问题1:极坐标下点M的坐标( ρ,θ )
求:点M关于极点,极轴的对称点?
