人教版A版选修4—4 2.2 圆锥曲线的参数方程(共21张ppt)
文档属性
| 名称 | 人教版A版选修4—4 2.2 圆锥曲线的参数方程(共21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 246.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-24 11:51:39 | ||
图片预览



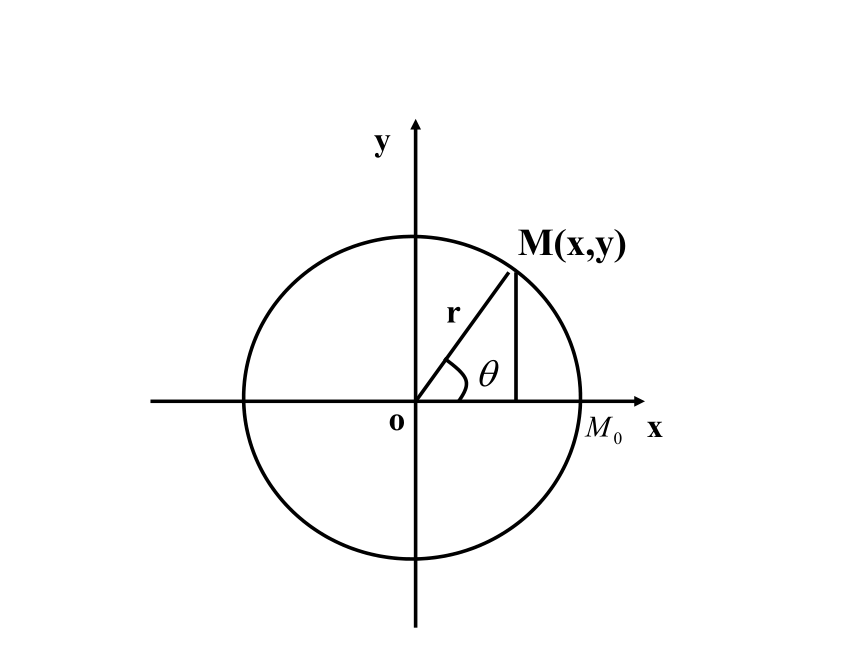





文档简介
课件21张PPT。圆锥曲线的参数方程
---椭圆、抛物线关于参数几点说明:
1.参数是联系变数x,y的桥梁,同一曲线选取参数不同, 曲线参数方程形式也不一样
2.在实际问题中要确定参数的取值范围复习1、参数方程的概念:复习2,圆的参数方程1.圆心在原点,半径为r的圆的参数方程:2.圆心为(a, b),半径为r的圆的参数方程:yxorM(x,y) 3,参数方程和普通方程的互化:1.代入法:利用解方程的技巧求出参数t,然后代入消
去参数
2.三角法:利用三角恒等式消去参数
3.整体消元法:根据参数方程本身的结构特征,从
整体上消去。化参数方程为普通方程为F(x,y)=0:在消参过程中注意变量x、y取值范围的一致性,必须根据参数的取值范围,确定f(t)和g(t)值域得x、y的取值范围。复习一、椭圆的参数方程如下图,以原点为圆心,分别以a,b(a>b>0)为半径作两个圆,点B是大圆半径OA与小圆的交点,过点A作AN⊥OX,垂足为N,过点B作BM⊥AN,垂足为M,求当半径OA绕点O旋转时点M的轨迹参数方程. 分析:点M的横坐标与点A的横坐标相同,点M的纵坐标与点B的纵坐标相同. 而A、B的坐标可以通过
引进参数建立联系. 设∠XOA=φ一、知识构建如下图,以原点为圆心,分别以a,b(a>b>0)为半径作两个圆,点B是大圆半径OA与小圆的交点,过点A作AN⊥OX,垂足为N,过点B作BM⊥AN,垂足为M,求当半径OA绕点O旋转时点M的轨迹参数方程. 解:设∠XOA=φ, M(x, y), 则A: (acosφ, a sinφ),B: (bcosφ, bsinφ),由已知:即为点M的轨迹参数方程.消去参数得:即为点M的轨迹普通方程.知识对比椭圆的标准方程:椭圆的参数方程中参数φ的几何意义:圆的标准方程:圆的参数方程: x2+y2=r2θ的几何意义是:OM的旋转角∠XOM=θ椭圆的参数方程:是半径OA的旋转角(点M的离心角);是∠XOA=φ.在椭圆的参数方程中,常数a、b分别是椭圆的长半轴长和短半轴长. a>b>0概 括:【练习1】把下列普通方程化为参数方程. 把下列参数方程化为普通方程巩固练习二、抛物线的参数方程以时刻 t 为参数的抛物线的参数方程:对于一般抛物线,怎样建立参数方程呢?以抛物线的普通方程为例,其中p为焦点到准线的距离。 设M(x, y)为抛物线上除顶点外的任意一点,以射线OM为终边的角记作α 显然,当α在 内变化时,点M在抛物线上运动,并且对于α的每一个值,在抛物线上都有唯一的点M与之对应,因此,可以取α为参数来探求抛物线的参数方程. 因为点M在α的终边上,根据三角函数定义可得由方程 (α为参数)这是抛物线(不包括顶点)的参数方程. 如果令 (α为参数) 当t=0时,上式表示的点正好就是抛物线的顶点(0,0),因此,当 时, (t为参数) 就表示整条抛物线.参数 t 表示抛物线上除顶点外的任意一点与原点连线的斜率的倒数. 例3 如图,O为原点,A,B为抛物线 上异于顶点的两动点,且OA⊥OB,OM⊥AB于M,求点M的轨迹方程.椭圆的标准方程:椭圆的参数方程:——离心角 注:在椭圆的参数方程中,常数a、 b分别是椭圆的长半轴长和短半轴长. a>b 为参数三、课堂总结抛物线的标准方程:抛物线的参数方程:(t为参数)注:参数 t 表示抛物线上除顶点外的任意一点与原点连线的斜率的倒数.
---椭圆、抛物线关于参数几点说明:
1.参数是联系变数x,y的桥梁,同一曲线选取参数不同, 曲线参数方程形式也不一样
2.在实际问题中要确定参数的取值范围复习1、参数方程的概念:复习2,圆的参数方程1.圆心在原点,半径为r的圆的参数方程:2.圆心为(a, b),半径为r的圆的参数方程:yxorM(x,y) 3,参数方程和普通方程的互化:1.代入法:利用解方程的技巧求出参数t,然后代入消
去参数
2.三角法:利用三角恒等式消去参数
3.整体消元法:根据参数方程本身的结构特征,从
整体上消去。化参数方程为普通方程为F(x,y)=0:在消参过程中注意变量x、y取值范围的一致性,必须根据参数的取值范围,确定f(t)和g(t)值域得x、y的取值范围。复习一、椭圆的参数方程如下图,以原点为圆心,分别以a,b(a>b>0)为半径作两个圆,点B是大圆半径OA与小圆的交点,过点A作AN⊥OX,垂足为N,过点B作BM⊥AN,垂足为M,求当半径OA绕点O旋转时点M的轨迹参数方程. 分析:点M的横坐标与点A的横坐标相同,点M的纵坐标与点B的纵坐标相同. 而A、B的坐标可以通过
引进参数建立联系. 设∠XOA=φ一、知识构建如下图,以原点为圆心,分别以a,b(a>b>0)为半径作两个圆,点B是大圆半径OA与小圆的交点,过点A作AN⊥OX,垂足为N,过点B作BM⊥AN,垂足为M,求当半径OA绕点O旋转时点M的轨迹参数方程. 解:设∠XOA=φ, M(x, y), 则A: (acosφ, a sinφ),B: (bcosφ, bsinφ),由已知:即为点M的轨迹参数方程.消去参数得:即为点M的轨迹普通方程.知识对比椭圆的标准方程:椭圆的参数方程中参数φ的几何意义:圆的标准方程:圆的参数方程: x2+y2=r2θ的几何意义是:OM的旋转角∠XOM=θ椭圆的参数方程:是半径OA的旋转角(点M的离心角);是∠XOA=φ.在椭圆的参数方程中,常数a、b分别是椭圆的长半轴长和短半轴长. a>b>0概 括:【练习1】把下列普通方程化为参数方程. 把下列参数方程化为普通方程巩固练习二、抛物线的参数方程以时刻 t 为参数的抛物线的参数方程:对于一般抛物线,怎样建立参数方程呢?以抛物线的普通方程为例,其中p为焦点到准线的距离。 设M(x, y)为抛物线上除顶点外的任意一点,以射线OM为终边的角记作α 显然,当α在 内变化时,点M在抛物线上运动,并且对于α的每一个值,在抛物线上都有唯一的点M与之对应,因此,可以取α为参数来探求抛物线的参数方程. 因为点M在α的终边上,根据三角函数定义可得由方程 (α为参数)这是抛物线(不包括顶点)的参数方程. 如果令 (α为参数) 当t=0时,上式表示的点正好就是抛物线的顶点(0,0),因此,当 时, (t为参数) 就表示整条抛物线.参数 t 表示抛物线上除顶点外的任意一点与原点连线的斜率的倒数. 例3 如图,O为原点,A,B为抛物线 上异于顶点的两动点,且OA⊥OB,OM⊥AB于M,求点M的轨迹方程.椭圆的标准方程:椭圆的参数方程:——离心角 注:在椭圆的参数方程中,常数a、 b分别是椭圆的长半轴长和短半轴长. a>b 为参数三、课堂总结抛物线的标准方程:抛物线的参数方程:(t为参数)注:参数 t 表示抛物线上除顶点外的任意一点与原点连线的斜率的倒数.
