湘教数学七上《3.4一元一次方程模型的应用(1)》(14张PPT)
文档属性
| 名称 | 湘教数学七上《3.4一元一次方程模型的应用(1)》(14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-26 10:34:20 | ||
图片预览





文档简介
课件14张PPT。3.4一元一次方程模型的应用(4)湘教版数学七年级(上)黄亭市镇中学 阳卫民
某自来水公司按如下规定收取水费:如果每月用水不超过10t,按每 吨1.5元收费;如果每月用水超过10t,超过部分按每吨2元收费.小明家9月份用水15t,小明家9月份水费是 元。
课前热身小明家11月份用水费是22.8元,小明家11月份用水多少吨?
为鼓励居民节约用水,某市出台了新的家庭用水收费标准,规定:所交水费分为标准内水费1.96 元/ t,超标部分水费2.94元/t. 某家庭6月份用水12t,需交水费27.44元.求该市规定的家庭月标准用水量.分析:本问题首先要分析所交水费27.44元中是否含有超标部分,
由于1.96×12 = 23.52(元),小于27.44元,
因此所交水费中含有超标部分的水费,即
月标准内水费+超标部分的水费=该月所交水费.解:设家庭月标准用水量为x t,根据等量关系得
1.96x +(12-x)×2.94 = 27.44
解得x = 8 .答:该市家庭月标准用水量为8 t.例4 现有树苗若干棵,计划栽在一段公路的一侧,
要求路的两端各栽1棵,并且每2棵树的间隔相等. 方案一:如果每隔5m栽1棵,则树苗缺21棵;方案二:如果每隔5.5m栽1棵,则树苗正好栽完.根据以上方案,请算出原有树苗的棵数和这段路的长度.分析 观察上面植树示意图,想一想:(1)相邻两树的间隔长与应植树的棵数有什么关系?
(2)相邻两树的间隔长、应植树棵数与路长有怎样的
数量关系?
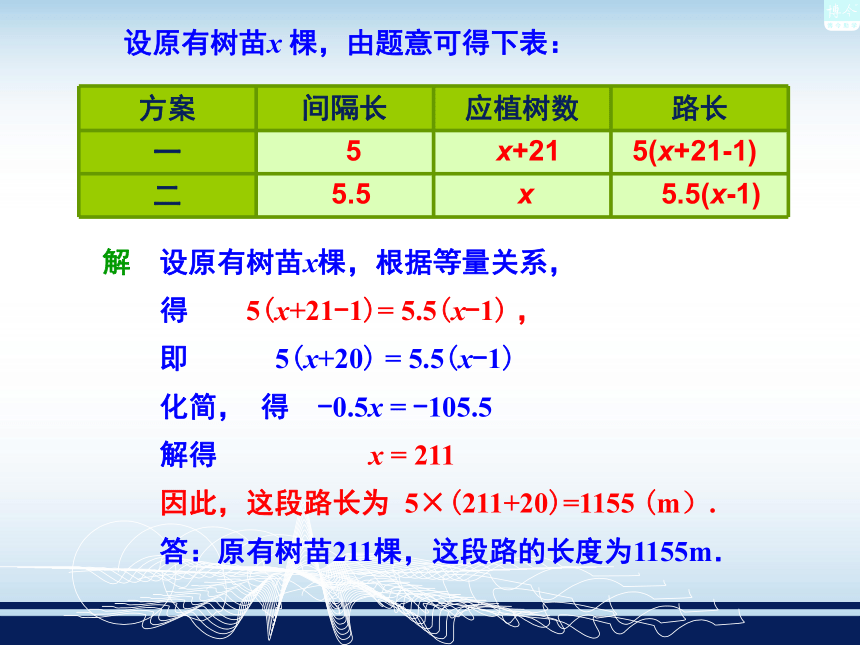
本题中涉及的等量关系有:方案一的路长=方案二的路长设原有树苗x 棵,由题意可得下表:解 设原有树苗x棵,根据等量关系,
得 5(x+21-1)= 5.5(x-1) ,
即 5(x+20) = 5.5(x-1)
化简, 得 -0.5x = -105.5
解得 x = 211
因此,这段路长为 5×(211+20)=1155 (m).
答:原有树苗211棵,这段路的长度为1155m.55.5
x+21
x5(x+21-1)5.5(x-1)
1. 为鼓励节约用电,某地用电收费标准规定:如果
每户每月用电不超过150 kW·h,那么1kW·h电按
0.5元缴纳; 超过部分则按1 kW·h电0.8元缴纳.
如果小张家某月缴纳的电费为147.8元,那么小张
家该月用电多少?答:小张家该月用电约241kw·h.2. 某道路一侧原有路灯106盏(两端都有),相邻两
盏灯的距离为36m,现计划全部更换为新型的节能
灯,且相邻两盏灯的距离变为70m,
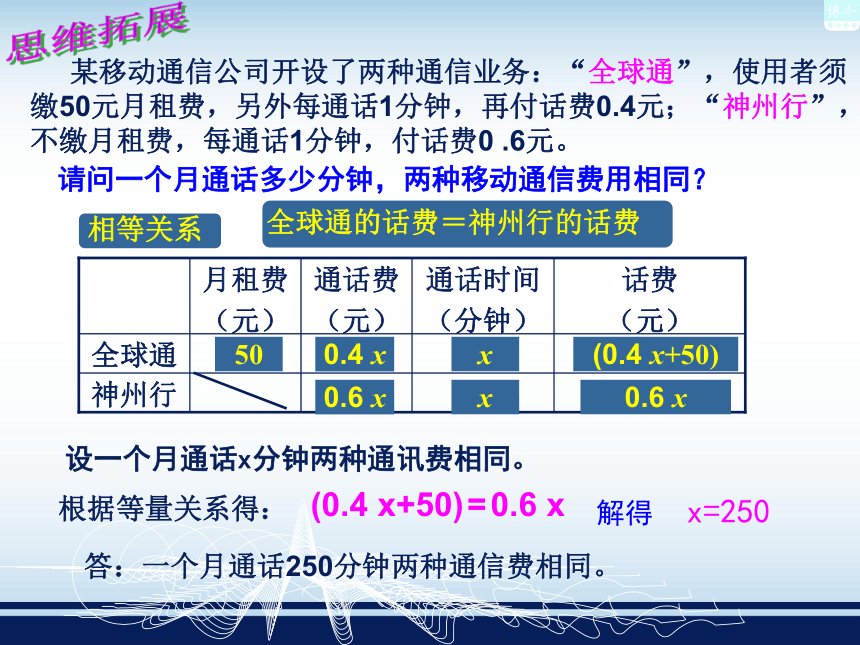
则需安装新型节能灯多少盏?答:需安装新型节能灯55盏. 某移动通信公司开设了两种通信业务:“全球通”,使用者须缴50元月租费,另外每通话1分钟,再付话费0.4元;“神州行”,不缴月租费,每通话1分钟,付话费0 .6元。50x0.4 x(0.4 x+50)x0.6 x0.6 x请问一个月通话多少分钟,两种移动通信费用相同?
根据等量关系得:设一个月通话x分钟两种通讯费相同。解得 x=250
答:一个月通话250分钟两种通信费相同。
思维拓展探索与创新500.4 x0.6 xxx(0.4 x+50)0.6 x由于一个月通话250分钟时,两种业务的话费相同,而在250分钟的基础上,通话每增加(或减少)1分钟, “全球通”和“神州行”的话费分别增加(或减少)0.4和0.6元。
所以,当每月通话时间超过250分钟时,选择“全球通”更省钱;
反之,当每月通话时间不足250分钟时,选择“神州行”更省钱。
曾老师利用假期带领部分同学到农村搞社会调查,每张车票原价是15元。甲车主说:“乘我的车可以打8折优惠。”;乙车主说:“乘我的车学生打9折,老师不买票。”曾老师心里计算了一下,觉得不论坐谁的车,车费都一样,请问:曾老师一共带了多少名学生?试一试15×0.811xx15×0.8x15×0.9x(12x+12)13.5x设曾老师带了x名学生。得下列数量关系表
学生数(人)
教师数(人)
解这个方程,得:x=8检验: x=8是原方程的解,且符合题意。答:曾老师一共带了8名学生。若这时,有一名同学突然接到电话说家里有事,不能前去,请问这时乘坐哪个车主的车划算?由于这时学生人数少于8人,所以乘坐乙车主的车更划算。解:设曾老师一共带了x名学生,依题意得:
学校食堂计划购买12张餐桌和一批餐椅,现在从“神农”和“丰泰”两大家具广场了解到:两个家具广场同一型号的餐桌和餐椅的报价都是200元和50元。另外,“神农”承诺:每购买一张餐桌赠送一把餐椅;“丰泰”承诺:所有桌椅都按报价的八五折销售。若食堂计划购买餐椅x把( x>12 )。 你能为食堂设计一个合理的采购方案吗?想一想121224002040xx50(x-12)42. 5x(50x-60+2400)(42. 5x+2040)我们首先要知道什么时候到这两个家具广场所需的费用相同。
7 .5x=240解,得: x=32检验: x=23是原方程的解,且符合题意。即买32把椅子时,到两家商场的费用相同。
由于在32把椅子的基础上,每增加(或减少)1把椅子,“神农”和“丰泰”的费用分别增加(或减少)50元和42 .5元。
所以,当购买椅子多于32把时,到“丰泰”购买更划算。反之,则到“神农”更划算。
解:解方程化简,得:
某百货商场元旦促销,购物不超过200元不优惠;超过200元,不足500元打9折;超过500元,其中500元打9折,超过部分打8折。某人这天两次购物分别用了110元和441元,问:(1) 此人两次购物时,如果其物品不打折,需要支付多少钱? (2)在此次活动中,他节省了多少钱? (3)如果同一天你到这家百货商场购买同样的货物,你会采取怎样的购买方案?并请求出你省下的钱数。思考解:(1)如果不打折,需要支付 600元。(2)在此次活动中,他节省了49元。(3)我将一次性买齐所有货物,这样可以节省70元。对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?畅所欲言
某自来水公司按如下规定收取水费:如果每月用水不超过10t,按每 吨1.5元收费;如果每月用水超过10t,超过部分按每吨2元收费.小明家9月份用水15t,小明家9月份水费是 元。
课前热身小明家11月份用水费是22.8元,小明家11月份用水多少吨?
为鼓励居民节约用水,某市出台了新的家庭用水收费标准,规定:所交水费分为标准内水费1.96 元/ t,超标部分水费2.94元/t. 某家庭6月份用水12t,需交水费27.44元.求该市规定的家庭月标准用水量.分析:本问题首先要分析所交水费27.44元中是否含有超标部分,
由于1.96×12 = 23.52(元),小于27.44元,
因此所交水费中含有超标部分的水费,即
月标准内水费+超标部分的水费=该月所交水费.解:设家庭月标准用水量为x t,根据等量关系得
1.96x +(12-x)×2.94 = 27.44
解得x = 8 .答:该市家庭月标准用水量为8 t.例4 现有树苗若干棵,计划栽在一段公路的一侧,
要求路的两端各栽1棵,并且每2棵树的间隔相等. 方案一:如果每隔5m栽1棵,则树苗缺21棵;方案二:如果每隔5.5m栽1棵,则树苗正好栽完.根据以上方案,请算出原有树苗的棵数和这段路的长度.分析 观察上面植树示意图,想一想:(1)相邻两树的间隔长与应植树的棵数有什么关系?
(2)相邻两树的间隔长、应植树棵数与路长有怎样的
数量关系?
本题中涉及的等量关系有:方案一的路长=方案二的路长设原有树苗x 棵,由题意可得下表:解 设原有树苗x棵,根据等量关系,
得 5(x+21-1)= 5.5(x-1) ,
即 5(x+20) = 5.5(x-1)
化简, 得 -0.5x = -105.5
解得 x = 211
因此,这段路长为 5×(211+20)=1155 (m).
答:原有树苗211棵,这段路的长度为1155m.55.5
x+21
x5(x+21-1)5.5(x-1)
1. 为鼓励节约用电,某地用电收费标准规定:如果
每户每月用电不超过150 kW·h,那么1kW·h电按
0.5元缴纳; 超过部分则按1 kW·h电0.8元缴纳.
如果小张家某月缴纳的电费为147.8元,那么小张
家该月用电多少?答:小张家该月用电约241kw·h.2. 某道路一侧原有路灯106盏(两端都有),相邻两
盏灯的距离为36m,现计划全部更换为新型的节能
灯,且相邻两盏灯的距离变为70m,
则需安装新型节能灯多少盏?答:需安装新型节能灯55盏. 某移动通信公司开设了两种通信业务:“全球通”,使用者须缴50元月租费,另外每通话1分钟,再付话费0.4元;“神州行”,不缴月租费,每通话1分钟,付话费0 .6元。50x0.4 x(0.4 x+50)x0.6 x0.6 x请问一个月通话多少分钟,两种移动通信费用相同?
根据等量关系得:设一个月通话x分钟两种通讯费相同。解得 x=250
答:一个月通话250分钟两种通信费相同。
思维拓展探索与创新500.4 x0.6 xxx(0.4 x+50)0.6 x由于一个月通话250分钟时,两种业务的话费相同,而在250分钟的基础上,通话每增加(或减少)1分钟, “全球通”和“神州行”的话费分别增加(或减少)0.4和0.6元。
所以,当每月通话时间超过250分钟时,选择“全球通”更省钱;
反之,当每月通话时间不足250分钟时,选择“神州行”更省钱。
曾老师利用假期带领部分同学到农村搞社会调查,每张车票原价是15元。甲车主说:“乘我的车可以打8折优惠。”;乙车主说:“乘我的车学生打9折,老师不买票。”曾老师心里计算了一下,觉得不论坐谁的车,车费都一样,请问:曾老师一共带了多少名学生?试一试15×0.811xx15×0.8x15×0.9x(12x+12)13.5x设曾老师带了x名学生。得下列数量关系表
学生数(人)
教师数(人)
解这个方程,得:x=8检验: x=8是原方程的解,且符合题意。答:曾老师一共带了8名学生。若这时,有一名同学突然接到电话说家里有事,不能前去,请问这时乘坐哪个车主的车划算?由于这时学生人数少于8人,所以乘坐乙车主的车更划算。解:设曾老师一共带了x名学生,依题意得:
学校食堂计划购买12张餐桌和一批餐椅,现在从“神农”和“丰泰”两大家具广场了解到:两个家具广场同一型号的餐桌和餐椅的报价都是200元和50元。另外,“神农”承诺:每购买一张餐桌赠送一把餐椅;“丰泰”承诺:所有桌椅都按报价的八五折销售。若食堂计划购买餐椅x把( x>12 )。 你能为食堂设计一个合理的采购方案吗?想一想121224002040xx50(x-12)42. 5x(50x-60+2400)(42. 5x+2040)我们首先要知道什么时候到这两个家具广场所需的费用相同。
7 .5x=240解,得: x=32检验: x=23是原方程的解,且符合题意。即买32把椅子时,到两家商场的费用相同。
由于在32把椅子的基础上,每增加(或减少)1把椅子,“神农”和“丰泰”的费用分别增加(或减少)50元和42 .5元。
所以,当购买椅子多于32把时,到“丰泰”购买更划算。反之,则到“神农”更划算。
解:解方程化简,得:
某百货商场元旦促销,购物不超过200元不优惠;超过200元,不足500元打9折;超过500元,其中500元打9折,超过部分打8折。某人这天两次购物分别用了110元和441元,问:(1) 此人两次购物时,如果其物品不打折,需要支付多少钱? (2)在此次活动中,他节省了多少钱? (3)如果同一天你到这家百货商场购买同样的货物,你会采取怎样的购买方案?并请求出你省下的钱数。思考解:(1)如果不打折,需要支付 600元。(2)在此次活动中,他节省了49元。(3)我将一次性买齐所有货物,这样可以节省70元。对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?畅所欲言
同课章节目录
