湘教数学七上《3.4一元一次方程模型的应用(3)》(84张PPT)
文档属性
| 名称 | 湘教数学七上《3.4一元一次方程模型的应用(3)》(84张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-26 13:13:11 | ||
图片预览







文档简介
(共84张PPT)
3.4一元一次方程的应用
怀化三中----肖丽
义务教育教科书数学七年级上册
怀化高铁
问题一:沪昆高铁长怀段路程约为420km,若高铁平均每小时行驶300km,从怀化到长沙约需 小时.
情景导入
1.4
问题二:速度、路程、时间之间的关系
路程=
时间=
速度=
速度×时间
路程÷速度
路程÷时间
复习回顾
精讲 例题
分 析
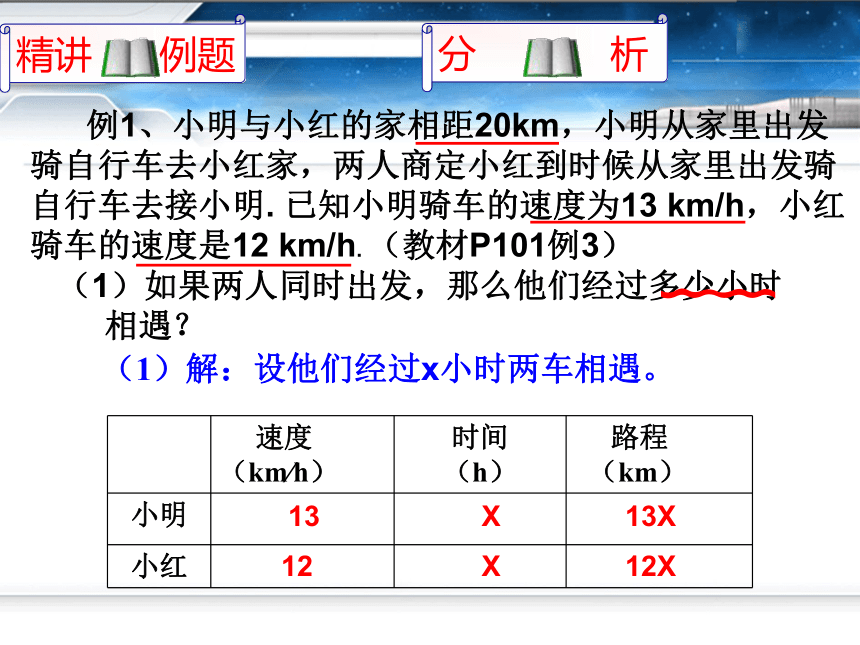
(1)解:设他们经过x小时两车相遇。
速度
(km∕h) 时间
(h) 路程
(km)
小明
小红
13
12
X
X
13X
12X
例1、小明与小红的家相距20km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为13 km/h,小红骑车的速度是12 km/h. (教材P101例3)
(1)如果两人同时出发,那么他们经过多少小时
相遇?
﹏
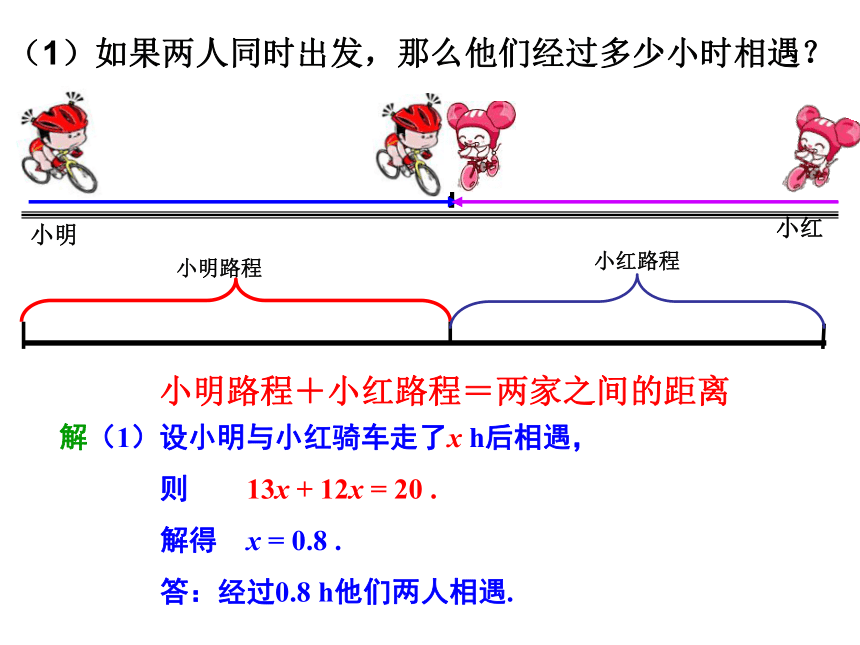
(1)如果两人同时出发,那么他们经过多少小时相遇?
小明
小明路程
小红路程
小明路程+小红路程=两家之间的距离
小红
解(1)设小明与小红骑车走了x h后相遇,
则 13x + 12x = 20 .
解得 x = 0.8 .
答:经过0.8 h他们两人相遇.
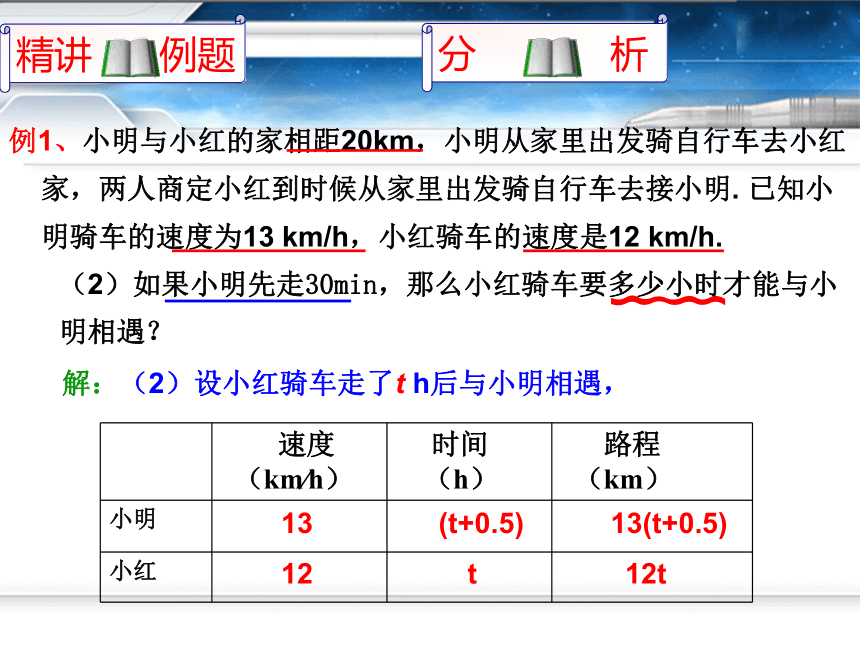
例1、小明与小红的家相距20km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为13 km/h,小红骑车的速度是12 km/h.
精讲 例题
分 析
解:(2)设小红骑车走了t h后与小明相遇,
速度
(km∕h) 时间
(h) 路程
(km)
小明
小红
13
12
(t+0.5)
t
13(t+0.5)
12t
﹏
(2)如果小明先走30min,那么小红骑车要多少小时才能与小明相遇?
(2)如果小明先走30min,那么小红骑车要多少小时才能与小明相遇?
小明
小红
小明先行路程
小红的路程
(小明先行路程+小明后行路程)+小红路程=总路程
小明后行路程
解(2)设小红骑车走了t h后与小明相遇,
则 13(0.5 + t )+12t = 20 .
解得 t = 0.54 .
答:小红骑车走0.54h后与小明相遇.
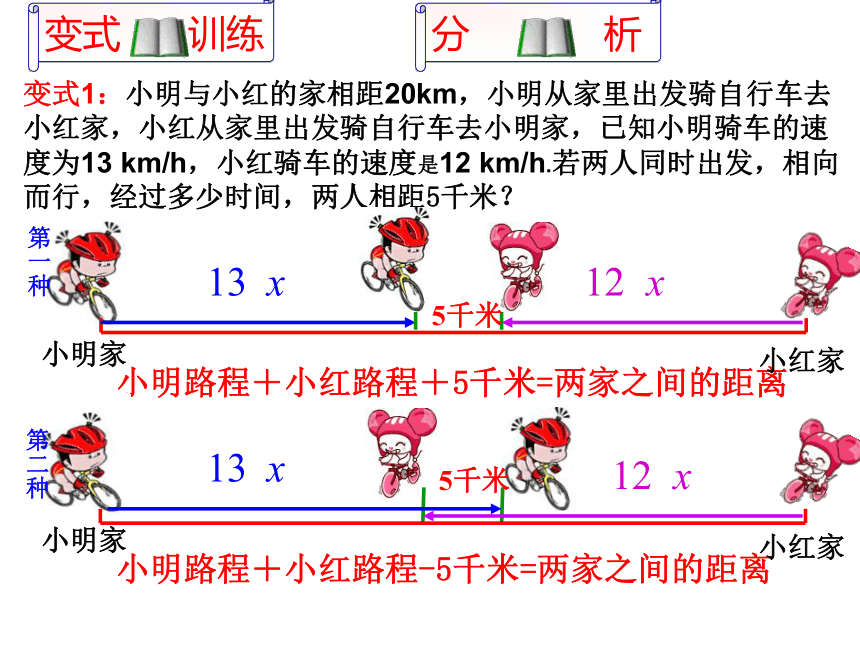
变式1:小明与小红的家相距20km,小明从家里出发骑自行车去小红家,小红从家里出发骑自行车去小明家,已知小明骑车的速度为13 km/h,小红骑车的速度是12 km/h.若两人同时出发,相向而行,经过多少时间,两人相距5千米?
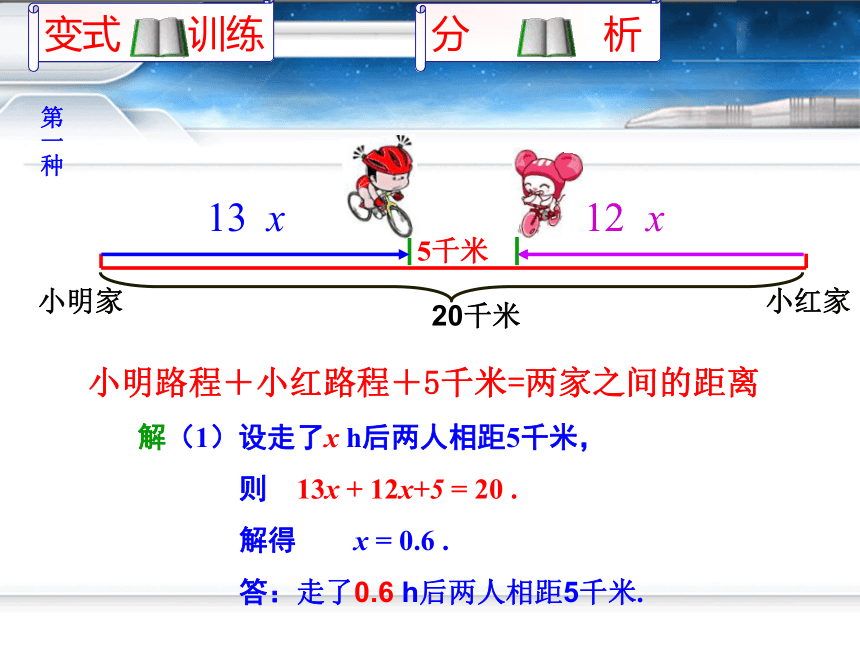
小明路程+小红路程+5千米=两家之间的距离
.
.
变式 训练
分 析
小明路程+小红路程-5千米=两家之间的距离
第一种
第二种
5千米
小明家
小红家
小明家
小红家
5千米
小明家
小红家
5千米
小明路程+小红路程+5千米=两家之间的距离
变式 训练
分 析
解(1)设走了x h后两人相距5千米,
则 13x + 12x+5 = 20 .
解得 x = 0.6 .
答:走了0.6 h后两人相距5千米.
第一种
20千米
变式 训练
分 析
小明家
小红家
5千米
小明路程+小红路程-5千米=两家之间的距离
第二种
解(1)设走了x h后两人相距5千米,
则 13x + 12x-5 = 20 .
解得 x = 1 .
答:走了1h后两人相距5千米.
20千米
变式2:小明、小红在400米长的环形跑道上练习跑步,小红每秒跑5米,小明每秒跑7.5米。
若两人同时同地反向出发,多长时间两人首次相遇?
变式 练习
分 析
反向
相等关系:
小明路程 + 小红路程 = 400
小明
小红
变式3:小明、小红在400米长的环形跑道上练习跑步,小红每秒跑5米,小明每秒跑7.5米。
变式 练习
分 析
同向
相等关系:
小明路程- 小红路程 = 400
小明
小红
若两人同时同地同向出发,多长时间两人首次相遇?
分组合作,勇夺第一
必做题 第1题 奇数组
第2题 偶数组
选做题 第3题 加分题
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
START
1. 甲乙两人骑自行车同时从相距65千 米的两地相向而行,经过2小时相遇。已知甲比乙每小时快2.5千米,求乙每小时行多少千米?
练习
2x+2(2.5+x) =65
x =15
解:设乙每小时行x千米。
答:乙每小时行15千米。
2、甲乙两人同时从两地骑自行车相向而行,甲每小时行15千米,乙每小时行13千米,两人在距中点3千米处相遇。求两地的距离。
练习
解法一:设两人x小时相遇。
则15x-3=13x+3
解之得x=3
(15+13)×3=84(千米)
答:两地的距离为84千米。
解法二:设两地的距离为S千米。
则
解之得S=84
答:两地的距离为84千米。
3、甲、乙两车从相距为180千米的A、B两地同时出发相向而行,已知甲的速度为每小时15千米,乙的速度为甲的3倍。问何时甲、乙两车相距60千米?
(1)行程问题中,路程、时间、速度存在着一个重要的等量关系: 路程=时间×速度
小结:
相遇问题相等关系:S甲+S乙=S总
(2)解决相遇行程问题应注意各段分路程与总路程之间的关系;
(3)在探索这类问题时,我们可以通过列表法和画线段图解决问题.
每课赠言
人生,没有选择,亦或是不可选择,你可以一走再走,而途中的转战,只是偶然的相遇,而人生的遇见是一个长久的过程,它需要慢慢地积累,所以你不必烦恼自己怎样,他人何想,而应当做则做,活在当下。
1.教材P102练习第1,2题。
2.学法大视野P58第2课时。
布置作业
再见!
3.4一元一次方程的应用
怀化三中----肖丽
义务教育教科书数学七年级上册
怀化高铁
问题一:沪昆高铁长怀段路程约为420km,若高铁平均每小时行驶300km,从怀化到长沙约需 小时.
情景导入
1.4
问题二:速度、路程、时间之间的关系
路程=
时间=
速度=
速度×时间
路程÷速度
路程÷时间
复习回顾
精讲 例题
分 析
(1)解:设他们经过x小时两车相遇。
速度
(km∕h) 时间
(h) 路程
(km)
小明
小红
13
12
X
X
13X
12X
例1、小明与小红的家相距20km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为13 km/h,小红骑车的速度是12 km/h. (教材P101例3)
(1)如果两人同时出发,那么他们经过多少小时
相遇?
﹏
(1)如果两人同时出发,那么他们经过多少小时相遇?
小明
小明路程
小红路程
小明路程+小红路程=两家之间的距离
小红
解(1)设小明与小红骑车走了x h后相遇,
则 13x + 12x = 20 .
解得 x = 0.8 .
答:经过0.8 h他们两人相遇.
例1、小明与小红的家相距20km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为13 km/h,小红骑车的速度是12 km/h.
精讲 例题
分 析
解:(2)设小红骑车走了t h后与小明相遇,
速度
(km∕h) 时间
(h) 路程
(km)
小明
小红
13
12
(t+0.5)
t
13(t+0.5)
12t
﹏
(2)如果小明先走30min,那么小红骑车要多少小时才能与小明相遇?
(2)如果小明先走30min,那么小红骑车要多少小时才能与小明相遇?
小明
小红
小明先行路程
小红的路程
(小明先行路程+小明后行路程)+小红路程=总路程
小明后行路程
解(2)设小红骑车走了t h后与小明相遇,
则 13(0.5 + t )+12t = 20 .
解得 t = 0.54 .
答:小红骑车走0.54h后与小明相遇.
变式1:小明与小红的家相距20km,小明从家里出发骑自行车去小红家,小红从家里出发骑自行车去小明家,已知小明骑车的速度为13 km/h,小红骑车的速度是12 km/h.若两人同时出发,相向而行,经过多少时间,两人相距5千米?
小明路程+小红路程+5千米=两家之间的距离
.
.
变式 训练
分 析
小明路程+小红路程-5千米=两家之间的距离
第一种
第二种
5千米
小明家
小红家
小明家
小红家
5千米
小明家
小红家
5千米
小明路程+小红路程+5千米=两家之间的距离
变式 训练
分 析
解(1)设走了x h后两人相距5千米,
则 13x + 12x+5 = 20 .
解得 x = 0.6 .
答:走了0.6 h后两人相距5千米.
第一种
20千米
变式 训练
分 析
小明家
小红家
5千米
小明路程+小红路程-5千米=两家之间的距离
第二种
解(1)设走了x h后两人相距5千米,
则 13x + 12x-5 = 20 .
解得 x = 1 .
答:走了1h后两人相距5千米.
20千米
变式2:小明、小红在400米长的环形跑道上练习跑步,小红每秒跑5米,小明每秒跑7.5米。
若两人同时同地反向出发,多长时间两人首次相遇?
变式 练习
分 析
反向
相等关系:
小明路程 + 小红路程 = 400
小明
小红
变式3:小明、小红在400米长的环形跑道上练习跑步,小红每秒跑5米,小明每秒跑7.5米。
变式 练习
分 析
同向
相等关系:
小明路程- 小红路程 = 400
小明
小红
若两人同时同地同向出发,多长时间两人首次相遇?
分组合作,勇夺第一
必做题 第1题 奇数组
第2题 偶数组
选做题 第3题 加分题
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
SEC
MIN
START
1. 甲乙两人骑自行车同时从相距65千 米的两地相向而行,经过2小时相遇。已知甲比乙每小时快2.5千米,求乙每小时行多少千米?
练习
2x+2(2.5+x) =65
x =15
解:设乙每小时行x千米。
答:乙每小时行15千米。
2、甲乙两人同时从两地骑自行车相向而行,甲每小时行15千米,乙每小时行13千米,两人在距中点3千米处相遇。求两地的距离。
练习
解法一:设两人x小时相遇。
则15x-3=13x+3
解之得x=3
(15+13)×3=84(千米)
答:两地的距离为84千米。
解法二:设两地的距离为S千米。
则
解之得S=84
答:两地的距离为84千米。
3、甲、乙两车从相距为180千米的A、B两地同时出发相向而行,已知甲的速度为每小时15千米,乙的速度为甲的3倍。问何时甲、乙两车相距60千米?
(1)行程问题中,路程、时间、速度存在着一个重要的等量关系: 路程=时间×速度
小结:
相遇问题相等关系:S甲+S乙=S总
(2)解决相遇行程问题应注意各段分路程与总路程之间的关系;
(3)在探索这类问题时,我们可以通过列表法和画线段图解决问题.
每课赠言
人生,没有选择,亦或是不可选择,你可以一走再走,而途中的转战,只是偶然的相遇,而人生的遇见是一个长久的过程,它需要慢慢地积累,所以你不必烦恼自己怎样,他人何想,而应当做则做,活在当下。
1.教材P102练习第1,2题。
2.学法大视野P58第2课时。
布置作业
再见!
同课章节目录
