人教版A版选修4—5 2.3 反证法(共15张ppt)
文档属性
| 名称 | 人教版A版选修4—5 2.3 反证法(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 189.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 19:00:56 | ||
图片预览





文档简介
课件15张PPT。反证法不等式的证明方法学习目标:?
1、了解反证法是间接证明的一种重要方法。
?2、理解反正法的思考过程与特点。
?3、掌握反正法的步骤。
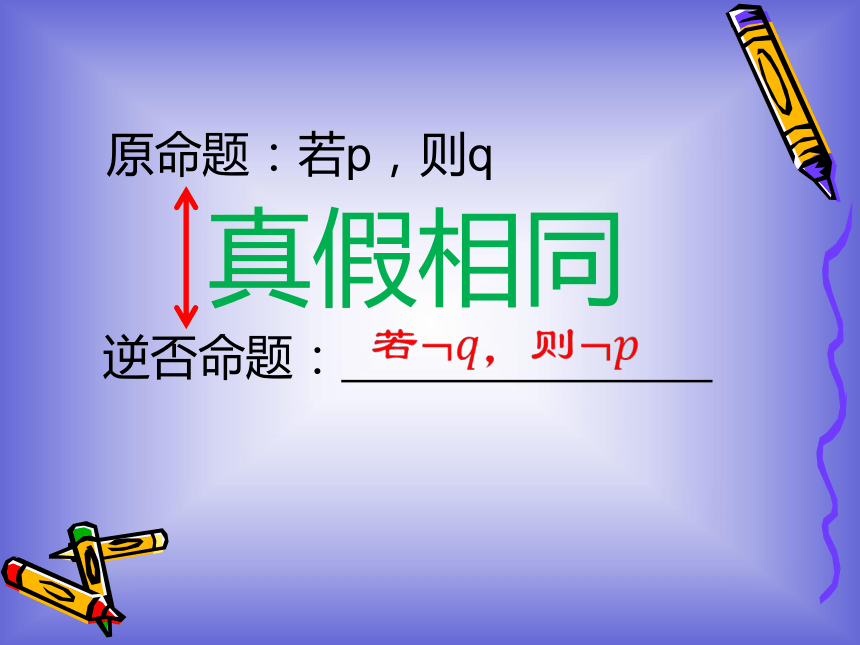
4、能利用反证法解决一些简单问题。原命题:若p,则q逆否命题: ?真假相同[读教材·填要点] 先假设 ,以此为出发点,结合已知条件,应用公理、定义、定理、性质等,进行正确的推理,得到和命题的条件(或已证明的定理、性质、明显成立的事实等)
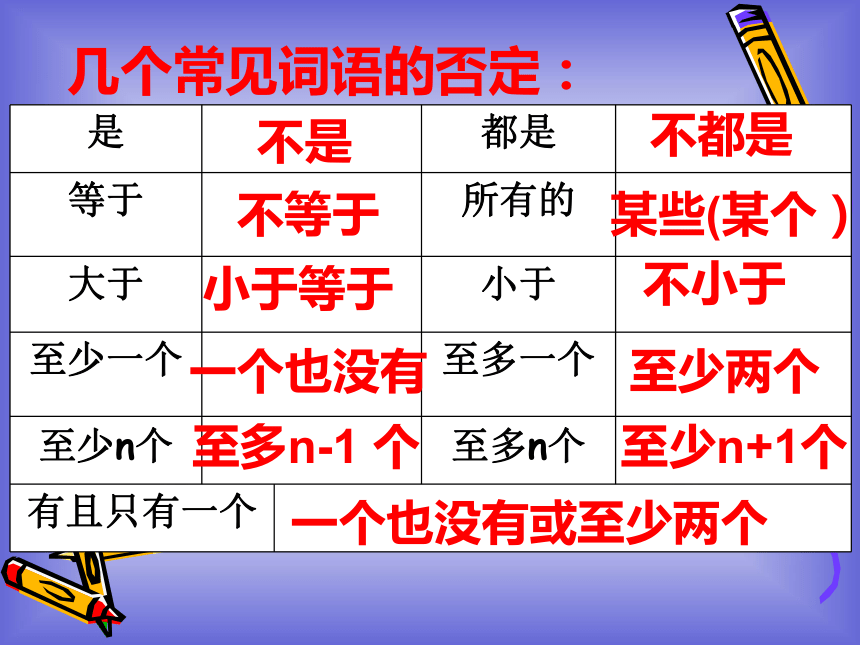
的结论,以说明 不正确,从而证明原命题成立,我们称这种证明问题的方法为反证法.要证的命题不成立矛盾假设几个常见词语的否定:不是不都是不等于某些(某个)小于等于不小于一个也没有至少两个至多n-1 个至少n+1个一个也没有或至少两个例1.已知:x, y>0, 且x+y>2。试证明:中至少有一个小于2。分析:于是考虑采用反证法。1.从下面证明这个结论,要分三种情况;2.结论的反面只有一种情况。证明因为x>0, y>0, 所以1+x≥2y, 1+y≥2x把这两个不等式相加,得
2+x+y≥2x+2y , 2≥x+y , 即 x+y≤2这与已知x+y>2相矛盾。因此,假设不成立即原命题成立。例1.已知:x, y>0, 且x+y>2。试证明:中至少有一个小于2。[小问题·大思维]1.用反证法证明不等式的步骤是什么? (1)反设:假设结论的否定成立。 (2)归谬:从假设出发进行正确的推理,得到一个
明显的矛盾。 (3)结论:由矛盾判定假设不成立,原命题成立。例2.已知a≠0,求证关于x的方程ax=b有且只有一个根。证明:?假设方程ax=b( a≠0 )至少存在两个根什么样的题适合用反证法:(1)含有“不是”,“不都”,“不存在”, “不可能”等否定性命题(2)含有“至少”,“至多”,“有且仅有”等存在性命题(3)直接证明方法难以下手的命题。[练习1]已知f(x)是R上的单调递增函数,f(a)+f(-b) < f(-a)
+f(b).求证:a<b.证明:假设a ≥ b , 则- a ≤- b , 即- b ≥ - a
于是有f(a) ≥ f(b),f(- b) ≥ f(- a),
∴f(a)+f(- b) ≥ f(b)+f(- a)与已知矛盾.
∴ 假设不成立 ∴ a < b.[练习2] 已知函数y=f(x)在区间(a,b)上是增函数,
求证:y=f(x)在区间(a,b)上至多有一个零点.证明:假设函数y=f(x)在区间(a,b)上至少有两个零点,
不妨设x1,x2(x1≠x2)为函数y=f(x)在区间(a,b)上的两个零点,且x1<x2,则f(x1)=f(x2)=0.
∵函数y=f(x)在区间(a,b)上为增函数,
x1,x2∈(a,b)且x1<x2,
∴f(x1)<f(x2),与f(x1)=f(x2)=0矛盾,
∴原假设不成立.
∴函数y=f(x)在(a,b)上至多有一个零点.? 反证法在高考中单独命题的可能性不大,一般以解答题一问的形式出现,但反证法是一种重要的思维模式,在填空选择中恰当的用反证法能快速而准确地得到正确答案。反证法在逻辑推理中,在现实中都有着广泛的应用.小结 2、在证明中含有 “否定性、存在性词语,或者直接证明
困难时,可使用反证法证明. 3、在证明中常见的矛盾可以与题设矛盾,也可以与已知
矛盾,与显然的事实矛盾,也可以自相矛盾.1、反证法步骤:(1)反设 (2) 归谬 (3)结论
1、了解反证法是间接证明的一种重要方法。
?2、理解反正法的思考过程与特点。
?3、掌握反正法的步骤。
4、能利用反证法解决一些简单问题。原命题:若p,则q逆否命题: ?真假相同[读教材·填要点] 先假设 ,以此为出发点,结合已知条件,应用公理、定义、定理、性质等,进行正确的推理,得到和命题的条件(或已证明的定理、性质、明显成立的事实等)
的结论,以说明 不正确,从而证明原命题成立,我们称这种证明问题的方法为反证法.要证的命题不成立矛盾假设几个常见词语的否定:不是不都是不等于某些(某个)小于等于不小于一个也没有至少两个至多n-1 个至少n+1个一个也没有或至少两个例1.已知:x, y>0, 且x+y>2。试证明:中至少有一个小于2。分析:于是考虑采用反证法。1.从下面证明这个结论,要分三种情况;2.结论的反面只有一种情况。证明因为x>0, y>0, 所以1+x≥2y, 1+y≥2x把这两个不等式相加,得
2+x+y≥2x+2y , 2≥x+y , 即 x+y≤2这与已知x+y>2相矛盾。因此,假设不成立即原命题成立。例1.已知:x, y>0, 且x+y>2。试证明:中至少有一个小于2。[小问题·大思维]1.用反证法证明不等式的步骤是什么? (1)反设:假设结论的否定成立。 (2)归谬:从假设出发进行正确的推理,得到一个
明显的矛盾。 (3)结论:由矛盾判定假设不成立,原命题成立。例2.已知a≠0,求证关于x的方程ax=b有且只有一个根。证明:?假设方程ax=b( a≠0 )至少存在两个根什么样的题适合用反证法:(1)含有“不是”,“不都”,“不存在”, “不可能”等否定性命题(2)含有“至少”,“至多”,“有且仅有”等存在性命题(3)直接证明方法难以下手的命题。[练习1]已知f(x)是R上的单调递增函数,f(a)+f(-b) < f(-a)
+f(b).求证:a<b.证明:假设a ≥ b , 则- a ≤- b , 即- b ≥ - a
于是有f(a) ≥ f(b),f(- b) ≥ f(- a),
∴f(a)+f(- b) ≥ f(b)+f(- a)与已知矛盾.
∴ 假设不成立 ∴ a < b.[练习2] 已知函数y=f(x)在区间(a,b)上是增函数,
求证:y=f(x)在区间(a,b)上至多有一个零点.证明:假设函数y=f(x)在区间(a,b)上至少有两个零点,
不妨设x1,x2(x1≠x2)为函数y=f(x)在区间(a,b)上的两个零点,且x1<x2,则f(x1)=f(x2)=0.
∵函数y=f(x)在区间(a,b)上为增函数,
x1,x2∈(a,b)且x1<x2,
∴f(x1)<f(x2),与f(x1)=f(x2)=0矛盾,
∴原假设不成立.
∴函数y=f(x)在(a,b)上至多有一个零点.? 反证法在高考中单独命题的可能性不大,一般以解答题一问的形式出现,但反证法是一种重要的思维模式,在填空选择中恰当的用反证法能快速而准确地得到正确答案。反证法在逻辑推理中,在现实中都有着广泛的应用.小结 2、在证明中含有 “否定性、存在性词语,或者直接证明
困难时,可使用反证法证明. 3、在证明中常见的矛盾可以与题设矛盾,也可以与已知
矛盾,与显然的事实矛盾,也可以自相矛盾.1、反证法步骤:(1)反设 (2) 归谬 (3)结论
