湘教数学七下2.1.2幂的乘方与积的乘方(1)课件(14张PPT)
文档属性
| 名称 | 湘教数学七下2.1.2幂的乘方与积的乘方(1)课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 280.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-26 00:00:00 | ||
图片预览





文档简介
课件14张PPT。问 题 同底数幂相乘法则是什么?幂的乘方运算法则?即:am · an = am+n (m,n都是正整数). 即:( am ) n = a mn(m,n都是正整数).2)幂的乘方,底数不变,指数相乘1)同底数幂相乘,底数不变,指数相加学练优七年级数学(XJ)
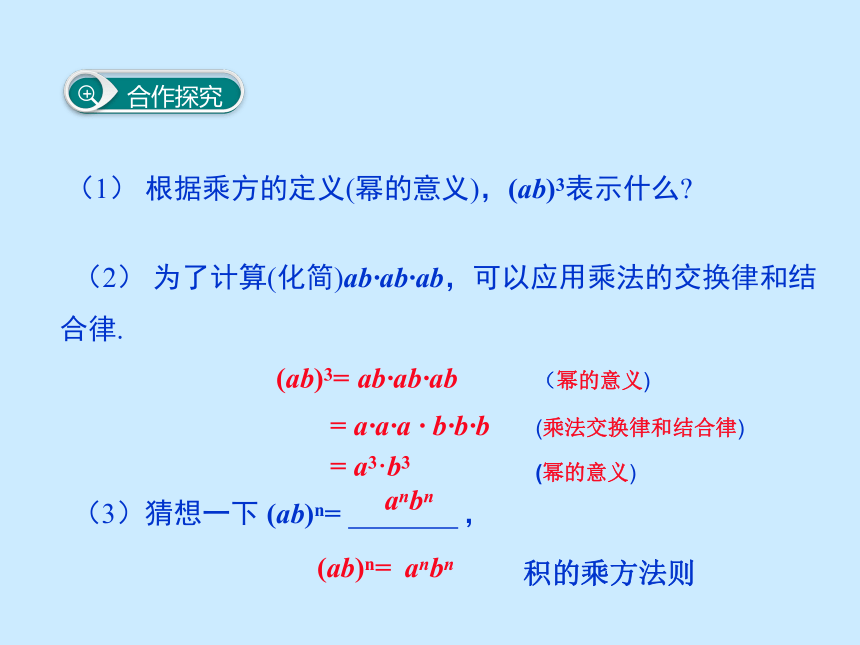
教学课件第2课时 积的乘方(ab)3=ab·ab·ab (2) 为了计算(化简)ab·ab·ab,可以应用乘法的交换律和结合律.= a·a·a · b·b·b= a3·b3(3)猜想一下 (ab)n= ,(1) 根据乘方的定义(幂的意义),(ab)3表示什么?(ab)n=anbnanbn
(幂的意义)
(乘法交换律和结合律)
(幂的意义)
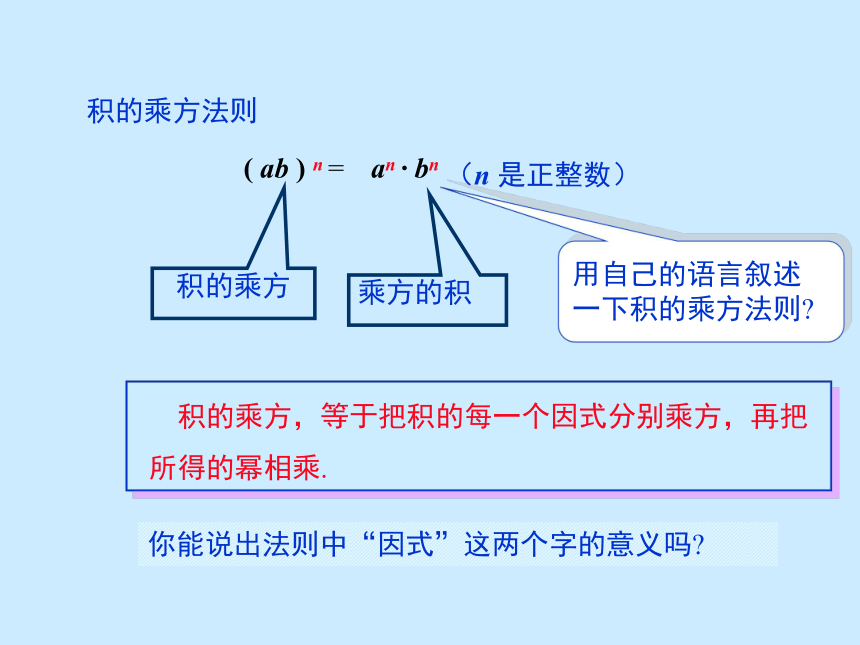
积的乘方法则 (ab)n = (ab) · (ab) · … · (ab)= (a · a · … ·a ) · (b · b · … ·b)= anbn (n为正整数). 怎样计算(ab)n ?在运算过程中你用到了哪些知识?(幂的意义)(乘法交换律和结合律)(幂的意义)计算(2b)3 (2b)3 =(2b)·(2b)·(2b) (幂的意义)=(2 · 2 · 2) · (b · b · b) (乘法交换律和结合律)= 23b3. (幂的意义)= 8b3. (乘方的运算)积的乘方乘方的积( ab ) n = an · bn(n 是正整数)积的乘方法则用自己的语言叙述一下积的乘方法则? 积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.你能说出法则中“因式”这两个字的意义吗? 公式的拓展 ( abc )n=an · bn · cn 三个或三个以上的积的乘方,是否也具有上面的性质? 怎样用公式表示?=32x2 = 9x2 ;(1) (3x)2(2) (-2b)5= (-2)5b5= -32b5 ;例1 计算:(3) (-2xy)4 = (-2)4 x4 y4=16x4 y4 ;1.-2(a2)3 · (a3)2 · a -(-a)2 ·(-a)3 · (a4)2.解: -2(a2)3 · (a3)2 · a-(-a)2 ·(-a)3 · (a4)2
= -2a6 · a6 · a –a2 ·(-a)3 ·a8
= -2a6+6+1 + a2+3+8
= -2a13+a13
= -a13.例2 计算: 2. 2(-a)2 · (b2)3 -3a2 ·(-b3)2.解:2(-a)2 · (b2)3 -3a2 ·(-b3)2= 2a2b6 -3a2b6= -a2b6.(1) (-2x)3 (2) (-4xy)2解: (-2x)3= (-2)3 · x3= -8x3.解: (-4xy)2= (-4)2 · x2 · y2= 16x2y2.1. 计算:(3) (xy2)3 解: (xy2)3= x3 · (y2)3= x3y6. (4) (-3ab2c3)4解:(-3ab2c3)4 = (-3)4 · a4 ·(b2)4 · (c3)4
= 81a4b8c122. 下面的计算对不对?如果不对,应怎样改正?(1)(ab3)2=ab6(2)(2xy)3=6x3y3答:不对,应是(ab3)2=a2b6.答:不对,应是(2xy)3=8x3y3 .3. 计算: -( xyz )4 + ( 2x2y2z2 )2.解: -(xyz )4 + (2x2y2z2 )2
= -x4y4z4 + 4x4y4z4
= 3x4y4z4. 试用简便方法计算:(ab)n = an·bn (n是正整数)逆向使用:an·bn = (ab)n (1) 23×53 = (2×5)3 = 103 (3) (-5)16 × (-2)15= (-5)×[(-5)×(-2)]15= -5×1015 ; (4) 24 × 44 ×(-0.125)4 = [2×4×(-0.125)]4= 14= 1 .(2) 28×58 = (2×5)8 = 108 (ab)n = an·bn (n是正整数)逆向使用:an·bn = (ab)n 积的乘方:(abc)n=an · bn · cn公式的拓展: 课堂练习:
课本P.34. 练习T1.T2.T3
作业布置:
学法大视野:P.24-25.课堂达标,课后提升
教学课件第2课时 积的乘方(ab)3=ab·ab·ab (2) 为了计算(化简)ab·ab·ab,可以应用乘法的交换律和结合律.= a·a·a · b·b·b= a3·b3(3)猜想一下 (ab)n= ,(1) 根据乘方的定义(幂的意义),(ab)3表示什么?(ab)n=anbnanbn
(幂的意义)
(乘法交换律和结合律)
(幂的意义)
积的乘方法则 (ab)n = (ab) · (ab) · … · (ab)= (a · a · … ·a ) · (b · b · … ·b)= anbn (n为正整数). 怎样计算(ab)n ?在运算过程中你用到了哪些知识?(幂的意义)(乘法交换律和结合律)(幂的意义)计算(2b)3 (2b)3 =(2b)·(2b)·(2b) (幂的意义)=(2 · 2 · 2) · (b · b · b) (乘法交换律和结合律)= 23b3. (幂的意义)= 8b3. (乘方的运算)积的乘方乘方的积( ab ) n = an · bn(n 是正整数)积的乘方法则用自己的语言叙述一下积的乘方法则? 积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.你能说出法则中“因式”这两个字的意义吗? 公式的拓展 ( abc )n=an · bn · cn 三个或三个以上的积的乘方,是否也具有上面的性质? 怎样用公式表示?=32x2 = 9x2 ;(1) (3x)2(2) (-2b)5= (-2)5b5= -32b5 ;例1 计算:(3) (-2xy)4 = (-2)4 x4 y4=16x4 y4 ;1.-2(a2)3 · (a3)2 · a -(-a)2 ·(-a)3 · (a4)2.解: -2(a2)3 · (a3)2 · a-(-a)2 ·(-a)3 · (a4)2
= -2a6 · a6 · a –a2 ·(-a)3 ·a8
= -2a6+6+1 + a2+3+8
= -2a13+a13
= -a13.例2 计算: 2. 2(-a)2 · (b2)3 -3a2 ·(-b3)2.解:2(-a)2 · (b2)3 -3a2 ·(-b3)2= 2a2b6 -3a2b6= -a2b6.(1) (-2x)3 (2) (-4xy)2解: (-2x)3= (-2)3 · x3= -8x3.解: (-4xy)2= (-4)2 · x2 · y2= 16x2y2.1. 计算:(3) (xy2)3 解: (xy2)3= x3 · (y2)3= x3y6. (4) (-3ab2c3)4解:(-3ab2c3)4 = (-3)4 · a4 ·(b2)4 · (c3)4
= 81a4b8c122. 下面的计算对不对?如果不对,应怎样改正?(1)(ab3)2=ab6(2)(2xy)3=6x3y3答:不对,应是(ab3)2=a2b6.答:不对,应是(2xy)3=8x3y3 .3. 计算: -( xyz )4 + ( 2x2y2z2 )2.解: -(xyz )4 + (2x2y2z2 )2
= -x4y4z4 + 4x4y4z4
= 3x4y4z4. 试用简便方法计算:(ab)n = an·bn (n是正整数)逆向使用:an·bn = (ab)n (1) 23×53 = (2×5)3 = 103 (3) (-5)16 × (-2)15= (-5)×[(-5)×(-2)]15= -5×1015 ; (4) 24 × 44 ×(-0.125)4 = [2×4×(-0.125)]4= 14= 1 .(2) 28×58 = (2×5)8 = 108 (ab)n = an·bn (n是正整数)逆向使用:an·bn = (ab)n 积的乘方:(abc)n=an · bn · cn公式的拓展: 课堂练习:
课本P.34. 练习T1.T2.T3
作业布置:
学法大视野:P.24-25.课堂达标,课后提升
