湘教版七年级数学下册2.1.4多项式的乘法(2)课件(共22张)
文档属性
| 名称 | 湘教版七年级数学下册2.1.4多项式的乘法(2)课件(共22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-26 00:00:00 | ||
图片预览






文档简介
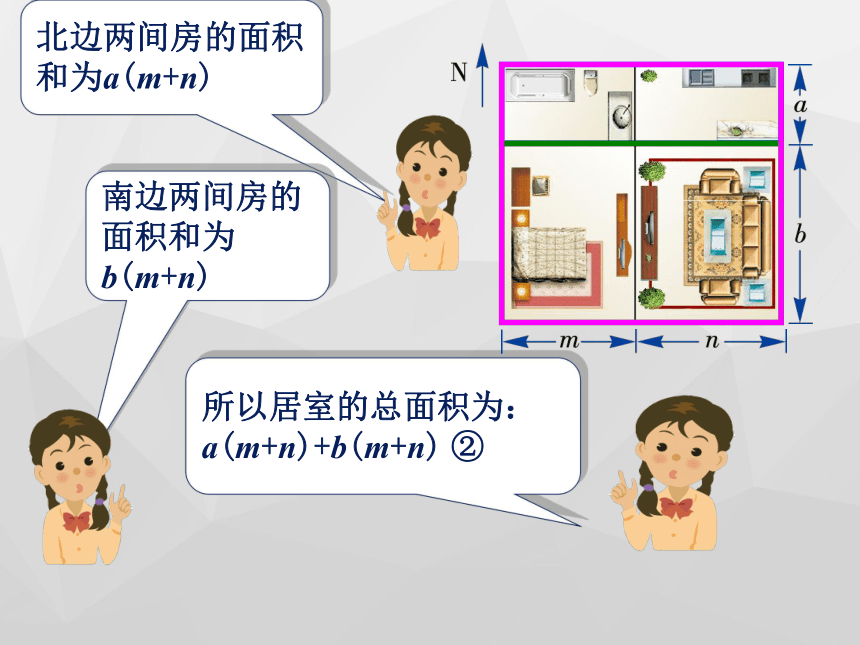
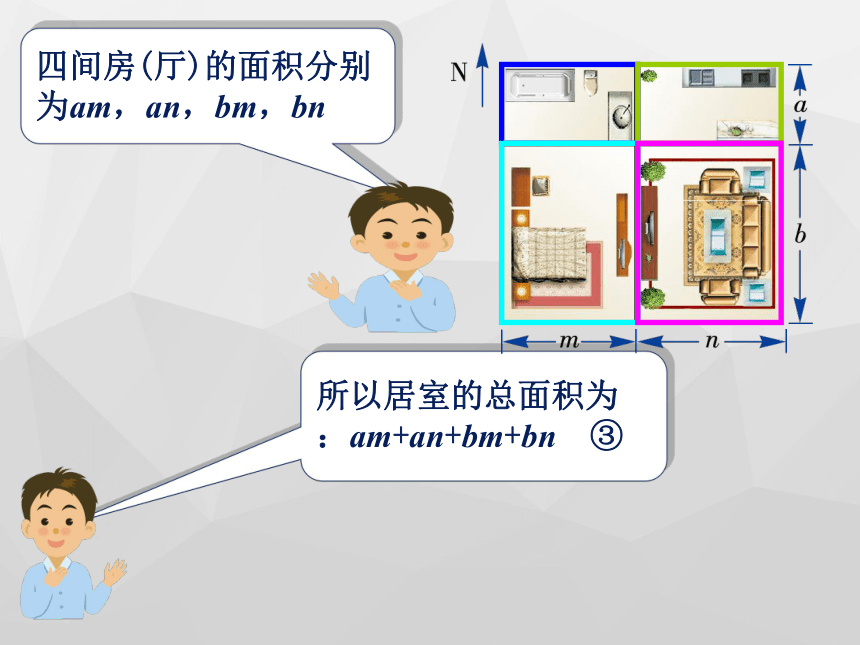
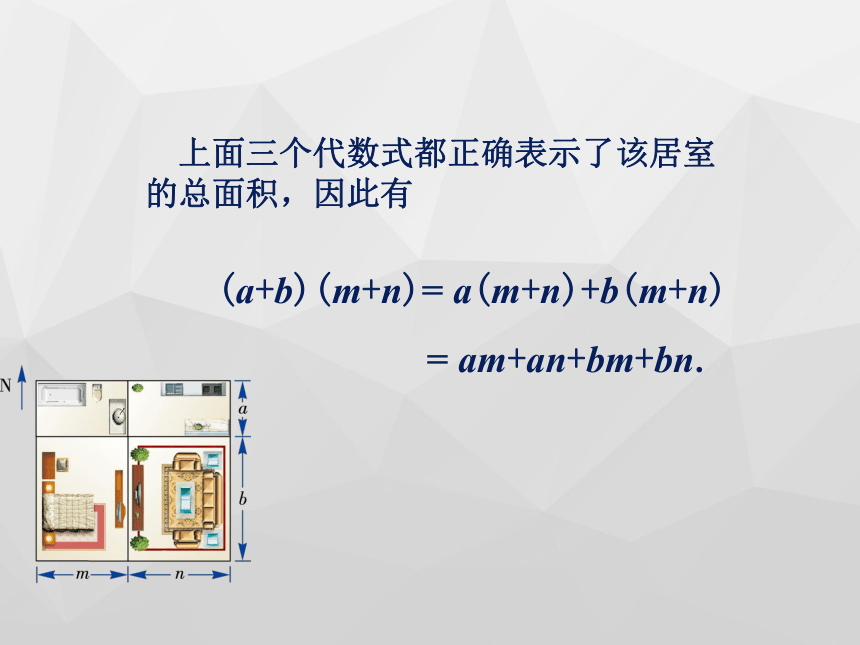
课件22张PPT。 2.1.4 多项式的乘法(第2课时)回顾 & 思考② 再把所得的积相加.① 将单项式分别乘以多项式的各项,进行单项式与多项式乘法运算时,要注意什么?① 不能漏乘:即单项式要乘遍多项式的每一项.② 去括号时注意符号的确定.同学们看(4)这道题怎样做?它和我们以前所学的有何不同? 计算: 有一套居室的平面图如图所示,怎样用代数式表示它的总面积呢?南北向总长为a+b东西向总长为m+n所以居室的总面积为:(a+b)·(m+n); ①北边两间房的面积和为a(m+n)南边两间房的面积和为b(m+n)所以居室的总面积为:a(m+n)+b(m+n) ②四间房(厅)的面积分别为am,an,bm,bn所以居室的总面积为:am+an+bm+bn ③这三个代数式之间有什么关系呢? (a+b)·(m+n) ① a(m+n)+b(m+n) ② am+an+bm+bn ③ 上面三个代数式都正确表示了该居室的总面积,因此有(a+b)(m+n)= a(m+n)+b(m+n)
= am+an+bm+bn. (a+b)(m+n)=am+an+bm+bn(a+b)(m+n)=am1234+an+bm+bn多项式的乘法法则:例12 计算:
(1)(2x+y)(x-3y);
(2)( 2x+1)(3x2-x-5);
(3)(x+a)(x+b). (1) (2x+y)(x-3y)解 (2x+y)(x-3y)= 2x · x + 2x ·(-3y)+ y · x + y ·(-3y)= 2x2-6xy+yx-3y2= 2x2-5xy-3y2(2) ( 2x+1)(3x2-x-5);解 (2x+1)(3x2-x-5)= 6x3-2x2–10x+3x2 -x-5= 6x3 + x2-11x - 5.解 (x+a)(x+b)= x2+bx+ax+ab=x2+(a+b)x +ab(3)(x+a)(x+b)第(3)小题的直观意义如图计算:
(1)(2x-2)(x+3);
(2) (x+1)(4x+5) ;
(3) (3x+4)(x-5) (1)(2x-2)(x+3)解:原式=2x2+6x-2x-6= 2x2-4x-6解:原式= 4x2+5x+4x+5=4 x2+9x+5 (2) (x+1)(4x+5) 解:原式= 3x2-15x+4x-20 (3)=3 x2-11x-20(3x+4)(x-5) 这节课,我的收获是……1、法则:多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。2、需要注意的几个问题
(1)漏乘
(2)符号问题
(3)最后结果应化成最简形式 先化简,再求值:
(1)(3x-1)(2 x +3)-(x-2)(6x-5) ,x=-3/8= 6x2+9x-2x -3-6x2+5x+12x-10) = 24x-13 当x=-3/8,原式=24 × (-3/8)-12=-22作 业P52 A组 4 谢 谢 大 家!
= am+an+bm+bn. (a+b)(m+n)=am+an+bm+bn(a+b)(m+n)=am1234+an+bm+bn多项式的乘法法则:例12 计算:
(1)(2x+y)(x-3y);
(2)( 2x+1)(3x2-x-5);
(3)(x+a)(x+b). (1) (2x+y)(x-3y)解 (2x+y)(x-3y)= 2x · x + 2x ·(-3y)+ y · x + y ·(-3y)= 2x2-6xy+yx-3y2= 2x2-5xy-3y2(2) ( 2x+1)(3x2-x-5);解 (2x+1)(3x2-x-5)= 6x3-2x2–10x+3x2 -x-5= 6x3 + x2-11x - 5.解 (x+a)(x+b)= x2+bx+ax+ab=x2+(a+b)x +ab(3)(x+a)(x+b)第(3)小题的直观意义如图计算:
(1)(2x-2)(x+3);
(2) (x+1)(4x+5) ;
(3) (3x+4)(x-5) (1)(2x-2)(x+3)解:原式=2x2+6x-2x-6= 2x2-4x-6解:原式= 4x2+5x+4x+5=4 x2+9x+5 (2) (x+1)(4x+5) 解:原式= 3x2-15x+4x-20 (3)=3 x2-11x-20(3x+4)(x-5) 这节课,我的收获是……1、法则:多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。2、需要注意的几个问题
(1)漏乘
(2)符号问题
(3)最后结果应化成最简形式 先化简,再求值:
(1)(3x-1)(2 x +3)-(x-2)(6x-5) ,x=-3/8= 6x2+9x-2x -3-6x2+5x+12x-10) = 24x-13 当x=-3/8,原式=24 × (-3/8)-12=-22作 业P52 A组 4 谢 谢 大 家!
