湘教版七年级数学下册2.2.2完全平方公式课件(21张)
文档属性
| 名称 | 湘教版七年级数学下册2.2.2完全平方公式课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-26 23:18:21 | ||
图片预览






文档简介
课件21张PPT。龙池实验中学湘教版七年级下册第二章完全平方公式李琪琦平方差公式
(a+b)(a-b)= a2-b2
两项的和乘以两项的差,等于两项的平方差
运用公式快速口答:(a+2)(a-2)
(1+2a)(1-2a)
(3a-5b)(3a+5b)
观察:(2a-3b)(2a-3b)能用平方差公式快速计算吗?
= a2-4 = 1-4a2= 9a2-25b2 =4a2-12ab+9b2
=4a2-6ab-6ab+9b2
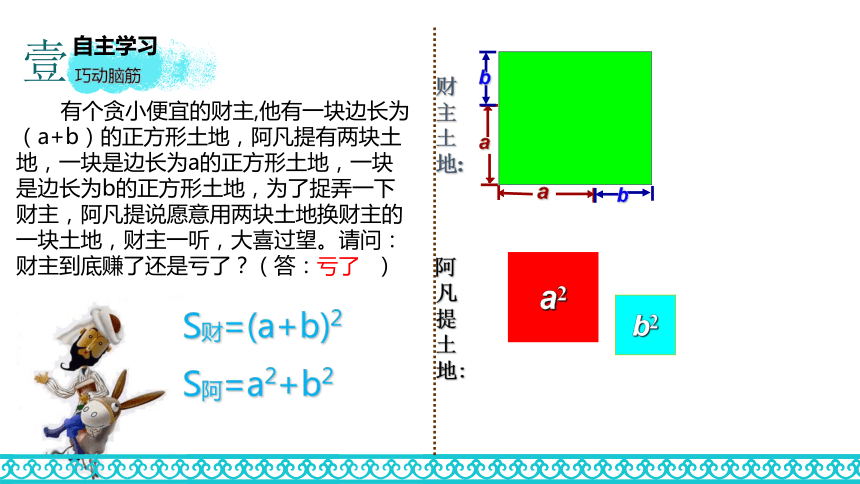
自主学习壹a2b2S财=(a+b)2
S阿=a2+b2 有个贪小便宜的财主,他有一块边长为(a+b)的正方形土地,阿凡提有两块土地,一块是边长为a的正方形土地,一块是边长为b的正方形土地,为了捉弄一下财主,阿凡提说愿意用两块土地换财主的一块土地,财主一听,大喜过望。请问:财主到底赚了还是亏了?(答: )自主学习巧动脑筋亏了a2b2财主土地
(a+b)2阿凡提土地
a2+b2a2b2亏了
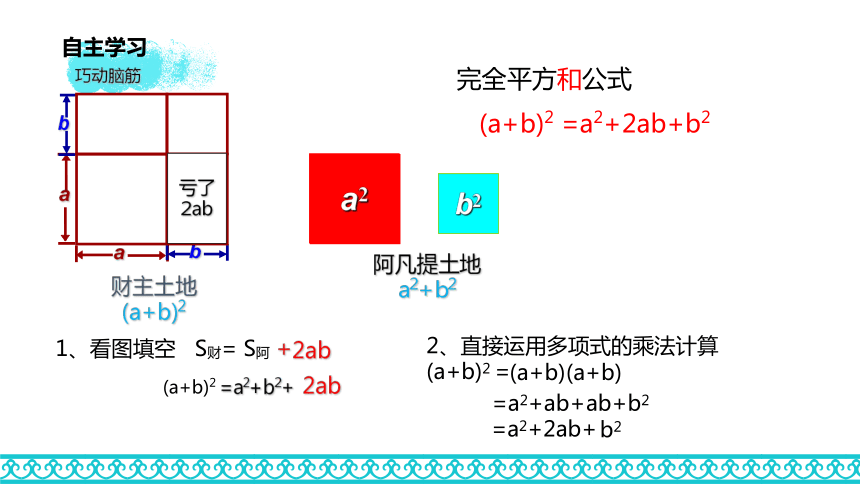
2ab
1、看图填空 S财= S阿 +
(a+b)2 =a2+b2+
2ab2、直接运用多项式的乘法计算(a+b)2 =2ab完全平方和公式
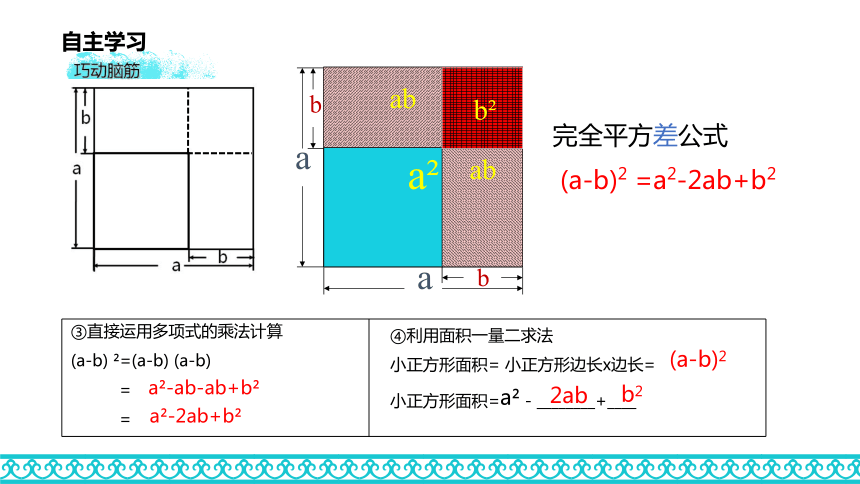
(a+b)2 =a2+2ab+b2自主学习巧动脑筋 a2-ab-ab+b2 a2-2ab+b2(a-b)22ab b2 ④利用面积一量二求法
小正方形面积= 小正方形边长x边长=
小正方形面积=a2 - ________+____完全平方差公式
(a-b)2 =a2-2ab+b2(a-b)2ababb2自主学习巧动脑筋(a+b)2 =a2+2ab+b2 两项和的平方,等于它们的平方和,加上它们的积的两倍
两项差的平方,等于它们的平方和,减去它们的积的两倍。
(a-b)2 =a2-2ab+b2公式特点:
它们的展开式都是由首项的平方、末项的平方、和首末的2倍构成
口诀: 首平方、末平方、两倍首末放中央完全平方和公式完全平方差公式自主学习发现规律思考:
公式中的“a”、“b”能换成其他数字或字母
甚至是单项式、整式吗?
(a +b)2 = a2 + 2 a b + b2 (-x - 2y)2 公式中的“a” “b”可以是任何整式!请判断,下列式子能用完全平方快速计算吗?
① (x + y)2 ② a2+b2
③ (2a + 3b)2 ④ (a+b-c)2√×√√
可以把a+b看成一个整体,
表示为(a+b)与c的差的平方;
也可以把b-c看成一个整体,
表示为a与(b-c)的和的平方。
合作探究 × 与平方差公式混淆,漏掉了首末积的2倍 × 应是首末积的2倍 × 结果应该是x2+2xy +y2 × 首平方应是4a2合作探究火眼金睛发现规律:1、符号的特点:在展开式中,首项和末项的平方符号均为 ;
若“a”“b” ,则展开式中“2ab”
若“a”“b” ,则展开式中“2ab” 同号 为正(同号为正)异号 为负(异号为负)正2、运用完全平方公式时应注意什么?(1)、完全平方公式要和平方差公式区分
(2)、完全平方公式的展开式有三项,别漏掉某一项
(3)、展开式中首项、末项的平方一定要是该项整体的平方
数形结合(a+b)2 =a2+2ab+b2(a-b)2 =a2-2ab+b2完全平方和公式完全平方差公式通过数与形之间的对应和转化来解决数学问题...转化思想 将未知的知识通过观察、分析、联想、类比等思维过程,选择恰当的方法进行变换,化归为已知知识...整体思想 发现问题的整体结构特征,善于用“集成”的眼光,把某些式子或图形看成一个整体...课堂归纳1、完全平方和公式 (a+b)2 =a2+2ab+b2
2、完全平方差公式 (a-b)2 =a2-2ab+b2
3、口诀:首平方、末平方、两倍首末随便放
4、注意:公式中的“a”“b” 可以是任何整式!课后提升课后拓展1、已知x2+k+4是完全平方展开式,则k=_____
A 、8x2 B 、4x C 、-4x D、±4x
2、已知 (a+b) 2 =25 ab=3 , 则 a2 + b2 =___
THANK
YOU下节课再见
(a+b)(a-b)= a2-b2
两项的和乘以两项的差,等于两项的平方差
运用公式快速口答:(a+2)(a-2)
(1+2a)(1-2a)
(3a-5b)(3a+5b)
观察:(2a-3b)(2a-3b)能用平方差公式快速计算吗?
= a2-4 = 1-4a2= 9a2-25b2 =4a2-12ab+9b2
=4a2-6ab-6ab+9b2
自主学习壹a2b2S财=(a+b)2
S阿=a2+b2 有个贪小便宜的财主,他有一块边长为(a+b)的正方形土地,阿凡提有两块土地,一块是边长为a的正方形土地,一块是边长为b的正方形土地,为了捉弄一下财主,阿凡提说愿意用两块土地换财主的一块土地,财主一听,大喜过望。请问:财主到底赚了还是亏了?(答: )自主学习巧动脑筋亏了a2b2财主土地
(a+b)2阿凡提土地
a2+b2a2b2亏了
2ab
1、看图填空 S财= S阿 +
(a+b)2 =a2+b2+
2ab2、直接运用多项式的乘法计算(a+b)2 =2ab完全平方和公式
(a+b)2 =a2+2ab+b2自主学习巧动脑筋 a2-ab-ab+b2 a2-2ab+b2(a-b)22ab b2 ④利用面积一量二求法
小正方形面积= 小正方形边长x边长=
小正方形面积=a2 - ________+____完全平方差公式
(a-b)2 =a2-2ab+b2(a-b)2ababb2自主学习巧动脑筋(a+b)2 =a2+2ab+b2 两项和的平方,等于它们的平方和,加上它们的积的两倍
两项差的平方,等于它们的平方和,减去它们的积的两倍。
(a-b)2 =a2-2ab+b2公式特点:
它们的展开式都是由首项的平方、末项的平方、和首末的2倍构成
口诀: 首平方、末平方、两倍首末放中央完全平方和公式完全平方差公式自主学习发现规律思考:
公式中的“a”、“b”能换成其他数字或字母
甚至是单项式、整式吗?
(a +b)2 = a2 + 2 a b + b2 (-x - 2y)2 公式中的“a” “b”可以是任何整式!请判断,下列式子能用完全平方快速计算吗?
① (x + y)2 ② a2+b2
③ (2a + 3b)2 ④ (a+b-c)2√×√√
可以把a+b看成一个整体,
表示为(a+b)与c的差的平方;
也可以把b-c看成一个整体,
表示为a与(b-c)的和的平方。
合作探究 × 与平方差公式混淆,漏掉了首末积的2倍 × 应是首末积的2倍 × 结果应该是x2+2xy +y2 × 首平方应是4a2合作探究火眼金睛发现规律:1、符号的特点:在展开式中,首项和末项的平方符号均为 ;
若“a”“b” ,则展开式中“2ab”
若“a”“b” ,则展开式中“2ab” 同号 为正(同号为正)异号 为负(异号为负)正2、运用完全平方公式时应注意什么?(1)、完全平方公式要和平方差公式区分
(2)、完全平方公式的展开式有三项,别漏掉某一项
(3)、展开式中首项、末项的平方一定要是该项整体的平方
数形结合(a+b)2 =a2+2ab+b2(a-b)2 =a2-2ab+b2完全平方和公式完全平方差公式通过数与形之间的对应和转化来解决数学问题...转化思想 将未知的知识通过观察、分析、联想、类比等思维过程,选择恰当的方法进行变换,化归为已知知识...整体思想 发现问题的整体结构特征,善于用“集成”的眼光,把某些式子或图形看成一个整体...课堂归纳1、完全平方和公式 (a+b)2 =a2+2ab+b2
2、完全平方差公式 (a-b)2 =a2-2ab+b2
3、口诀:首平方、末平方、两倍首末随便放
4、注意:公式中的“a”“b” 可以是任何整式!课后提升课后拓展1、已知x2+k+4是完全平方展开式,则k=_____
A 、8x2 B 、4x C 、-4x D、±4x
2、已知 (a+b) 2 =25 ab=3 , 则 a2 + b2 =___
THANK
YOU下节课再见
