1.1 独立性检验 课件(19张PPT)
文档属性
| 名称 | 1.1 独立性检验 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 509.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 19:17:57 | ||
图片预览





文档简介
课件19张PPT。1.1 独立性检验小概率事件的发生?高中生恋爱对学习成绩有影响吗?
高中流行这样一句话“文科就怕数学不好,理科就怕英语不好.”试问:文科学生总成绩不好与数学成绩不好有关系吗?
学生的性别与认为作业量大有关吗?
高中生吸烟对学习成绩有影响吗?
吸烟与患慢性气管炎有关吗?你能说说下面两个变量之间有关系吗?2019/7/25两事件独立的概念: 一般地,对于两个事件A,B,如果有P(AB)=P(A)P(B),就称事件A与B相互独立.举例:
1.分别掷两枚均匀的硬币,A={硬币甲出现正面}
B={硬币乙出现正面},则事件A与B的关系?
2.掷一颗质地均匀的骰子一次,A={掷出偶数点} B={掷出3的倍数点},则A与B,那么A与B的关系呢?
一般情况下,如果事件A与B相互独立,那么A与B,A与B,A与B也是相互独立的.
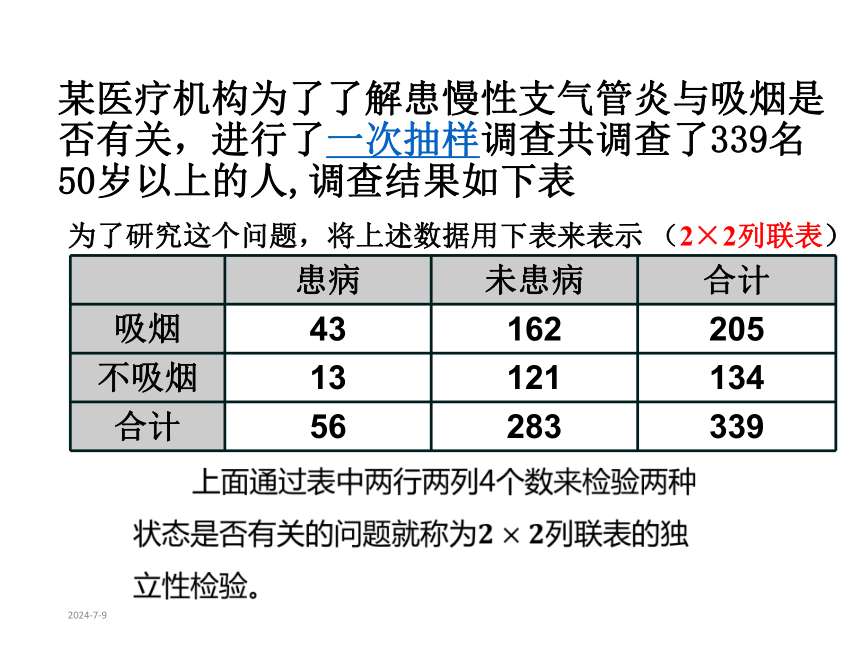
2019/7/25某医疗机构为了了解患慢性支气管炎与吸烟是否有关,进行了一次抽样调查共调查了339名50岁以上的人,调查结果如下表为了研究这个问题,将上述数据用下表来表示 (2×2列联表)
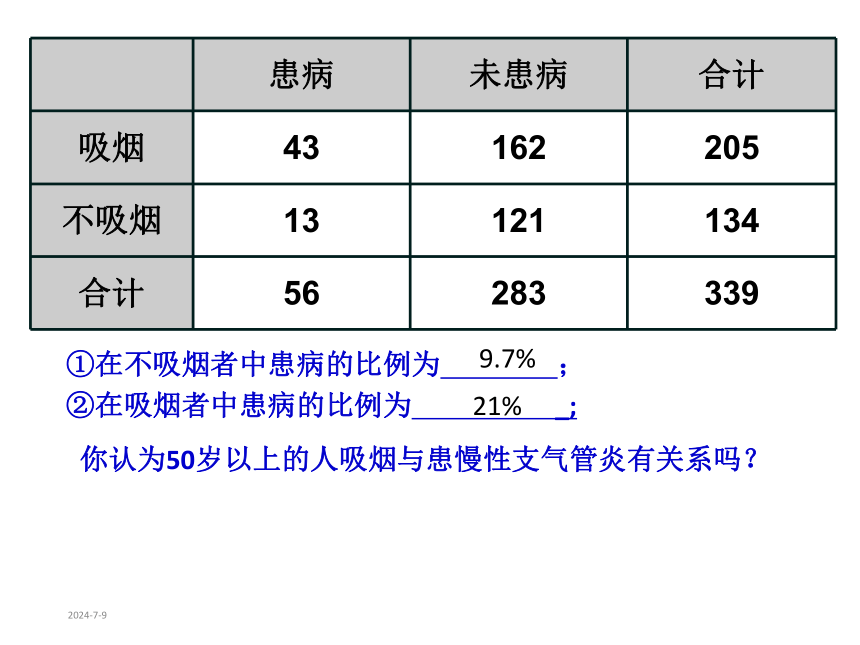
2019/7/25①在不吸烟者中患病的比例为 ;②在吸烟者中患病的比例为 _; 你认为50岁以上的人吸烟与患慢性支气管炎有关系吗? 9.7%21%2019/7/25①在不吸烟者中患病的比例为 ;②在吸烟者中患病的比例为 _; 吸烟群体和不吸烟群体患病的可能性存在差异40%66.7%28.6%31.9%为了使不同样本容量的数据有统一的评判标准,并且能够知道自己有多大把握做出判断,我们构造了一个随机变量
1.不同的样本,数据不同,比例不同,数据所体现的差异性不同,怎样针对不同样本数据设置统一的评判标准?2.针对不同的样本数据,可能做出不同的判断,那么你有多大的把握认为自己的判断是正确的?
2019/7/25 我们先假设 H0 :患病与吸烟没有关系为了得到一般性结论将表中“观测值”用字母表示,则得下列2×2列联表:2019/7/25若事件A与B没有关系,即A与B相互独立这时应该有P(AB)=P(A)P(B)成立.也就有下面三个式子成立:根据概率的统计定义,上面提到的众多事件的概率都可以用相应的频率来估计.P(AB)的估计为P(A)的估计为 ,P(B)的估计为 于是 与 应该很接近,或者说比较小.2019/7/25 应该比较小.同理由得得得2019/7/25也应该比较小.卡方χ2统计量公式: 认为事件A与事件B是无关的.2019/7/25例3: 对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行3年跟踪研究,调查他们是否又发作过心脏病,调查结果如下表所示: 试根据上述数据比较两种手术对病人又发作心脏病的影响有没有差别。2019/7/25解:这是一个2×2列联表的独立性检验问题,由公式 因为1.780<3.841,我们没有理由说“心脏搭桥手术”与“又发生过心脏病”有关,可以认为病人又发作心脏病与否跟他做过何种手术无关。 2019/7/25步骤2019/7/25
(1)在吸烟与患肺病是否有关的检验中,下列说法正确 的是 ( )
A.若χ2>6.635,则有99%的把握认为吸烟与患肺病有关,那么100名吸烟者中,有99个患肺病。
B.从独立性检验可知,有99%的把握认为吸烟与患肺病有关时,可以说某人吸烟,那么他有99%的可能性患肺病。
C.若从统计数据中求出有95%的把握认为吸烟与患肺病有关,是指有5%的可能性使推断出现错误。
D.以上三种说法都不对。
检测 C2019/7/25为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中随机抽取500名学生,得到如下列联表:
单位:人
能够有95%的把握认为高中生的性别与是否喜欢数学课程之间有关系吗?2019/7/252019/7/25小结(1)认识2×2列联表;
(2)知道独立性检验的基本思想;
(3)根据独立性检验的操作步骤,能对简单的2×2列联表中的两种状态进行独立性检验。作业:确定一个你感兴趣的问题,自己设计抽样方案,讨论调查的两个变量之间是否有关系2019/7/25
高中流行这样一句话“文科就怕数学不好,理科就怕英语不好.”试问:文科学生总成绩不好与数学成绩不好有关系吗?
学生的性别与认为作业量大有关吗?
高中生吸烟对学习成绩有影响吗?
吸烟与患慢性气管炎有关吗?你能说说下面两个变量之间有关系吗?2019/7/25两事件独立的概念: 一般地,对于两个事件A,B,如果有P(AB)=P(A)P(B),就称事件A与B相互独立.举例:
1.分别掷两枚均匀的硬币,A={硬币甲出现正面}
B={硬币乙出现正面},则事件A与B的关系?
2.掷一颗质地均匀的骰子一次,A={掷出偶数点} B={掷出3的倍数点},则A与B,那么A与B的关系呢?
一般情况下,如果事件A与B相互独立,那么A与B,A与B,A与B也是相互独立的.
2019/7/25某医疗机构为了了解患慢性支气管炎与吸烟是否有关,进行了一次抽样调查共调查了339名50岁以上的人,调查结果如下表为了研究这个问题,将上述数据用下表来表示 (2×2列联表)
2019/7/25①在不吸烟者中患病的比例为 ;②在吸烟者中患病的比例为 _; 你认为50岁以上的人吸烟与患慢性支气管炎有关系吗? 9.7%21%2019/7/25①在不吸烟者中患病的比例为 ;②在吸烟者中患病的比例为 _; 吸烟群体和不吸烟群体患病的可能性存在差异40%66.7%28.6%31.9%为了使不同样本容量的数据有统一的评判标准,并且能够知道自己有多大把握做出判断,我们构造了一个随机变量
1.不同的样本,数据不同,比例不同,数据所体现的差异性不同,怎样针对不同样本数据设置统一的评判标准?2.针对不同的样本数据,可能做出不同的判断,那么你有多大的把握认为自己的判断是正确的?
2019/7/25 我们先假设 H0 :患病与吸烟没有关系为了得到一般性结论将表中“观测值”用字母表示,则得下列2×2列联表:2019/7/25若事件A与B没有关系,即A与B相互独立这时应该有P(AB)=P(A)P(B)成立.也就有下面三个式子成立:根据概率的统计定义,上面提到的众多事件的概率都可以用相应的频率来估计.P(AB)的估计为P(A)的估计为 ,P(B)的估计为 于是 与 应该很接近,或者说比较小.2019/7/25 应该比较小.同理由得得得2019/7/25也应该比较小.卡方χ2统计量公式: 认为事件A与事件B是无关的.2019/7/25例3: 对196个接受心脏搭桥手术的病人和196个接受血管清障手术的病人进行3年跟踪研究,调查他们是否又发作过心脏病,调查结果如下表所示: 试根据上述数据比较两种手术对病人又发作心脏病的影响有没有差别。2019/7/25解:这是一个2×2列联表的独立性检验问题,由公式 因为1.780<3.841,我们没有理由说“心脏搭桥手术”与“又发生过心脏病”有关,可以认为病人又发作心脏病与否跟他做过何种手术无关。 2019/7/25步骤2019/7/25
(1)在吸烟与患肺病是否有关的检验中,下列说法正确 的是 ( )
A.若χ2>6.635,则有99%的把握认为吸烟与患肺病有关,那么100名吸烟者中,有99个患肺病。
B.从独立性检验可知,有99%的把握认为吸烟与患肺病有关时,可以说某人吸烟,那么他有99%的可能性患肺病。
C.若从统计数据中求出有95%的把握认为吸烟与患肺病有关,是指有5%的可能性使推断出现错误。
D.以上三种说法都不对。
检测 C2019/7/25为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中随机抽取500名学生,得到如下列联表:
单位:人
能够有95%的把握认为高中生的性别与是否喜欢数学课程之间有关系吗?2019/7/252019/7/25小结(1)认识2×2列联表;
(2)知道独立性检验的基本思想;
(3)根据独立性检验的操作步骤,能对简单的2×2列联表中的两种状态进行独立性检验。作业:确定一个你感兴趣的问题,自己设计抽样方案,讨论调查的两个变量之间是否有关系2019/7/25
