1.2 回归分析 课件(28张PPT)
文档属性
| 名称 | 1.2 回归分析 课件(28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 19:20:07 | ||
图片预览





文档简介
课件28张PPT。1.2 回归分析山东省昌乐及第中学 李秀梅人教B版选修1-21.2 回 归 分 析
教B版选修1-2学习目标
1、知道最小二乘法的思想,利用散点图分析两个变量是否存在相关关系,利用合适的回归模型求回归方程.
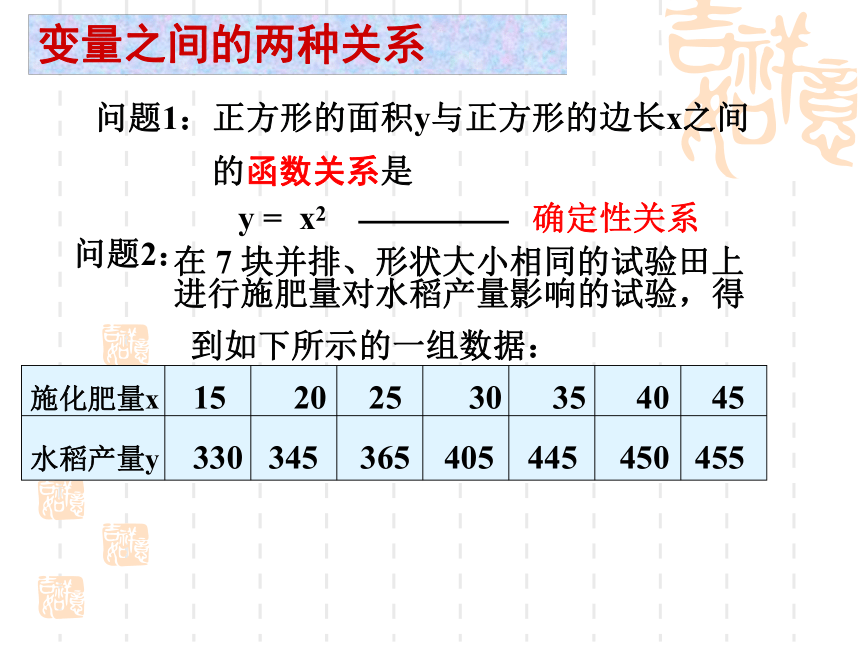
2、会用相关系数r,进行线性相关性检验问题1:正方形的面积y与正方形的边长x之间
的函数关系是y = x2问题2:在 7 块并排、形状大小相同的试验田上 进行施肥量对水稻产量影响的试验,得
到如下所示的一组数据:变量之间的两种关系 10 20 30 40 50500
450
400
350
300·······施化肥量水稻产量施化肥量x与水稻y具有的关系是相关关系是一种非确定的关系
现实生活中存在着大量的相关关系。
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入等等对具有相关关系的两个变量进行统计分析的方法叫回归分析。10 20 30 40 50500
450
400
350
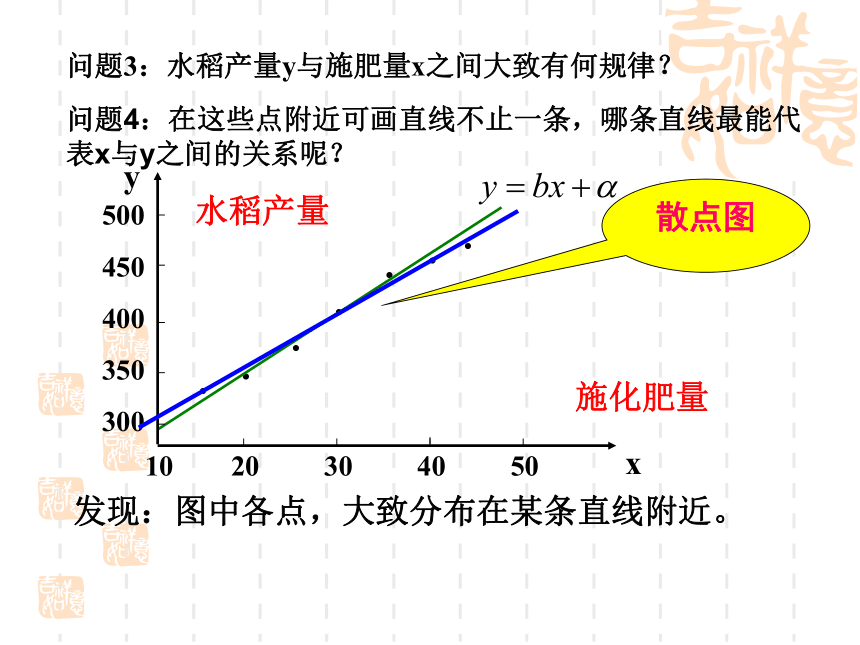
300·······发现:图中各点,大致分布在某条直线附近。散点图施化肥量水稻产量问题3:水稻产量y与施肥量x之间大致有何规律?
问题4:在这些点附近可画直线不止一条,哪条直线最能代表x与y之间的关系呢?
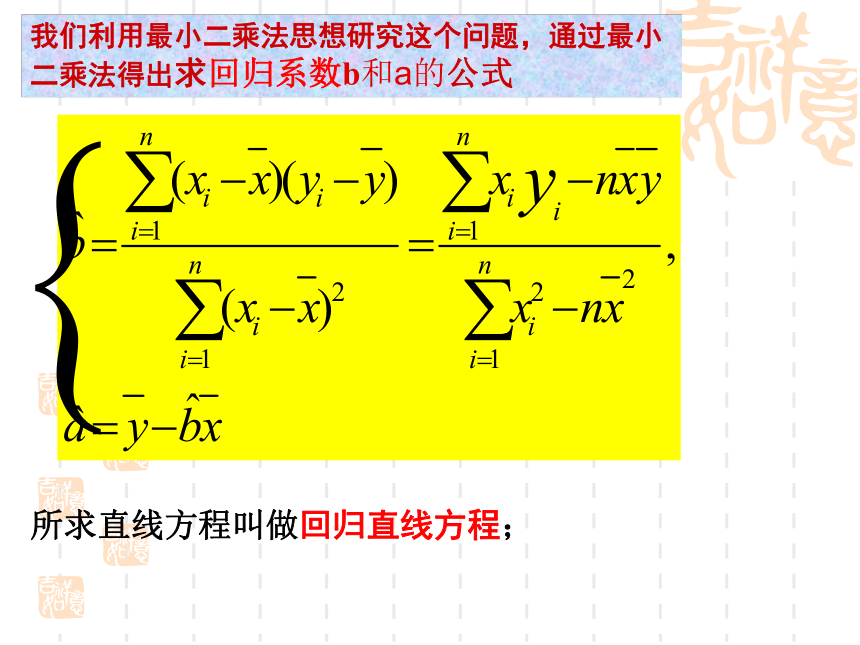
我们利用最小二乘法思想研究这个问题,通过最小二乘法得出求回归系数b和a的公式所求直线方程叫做回归直线方程;
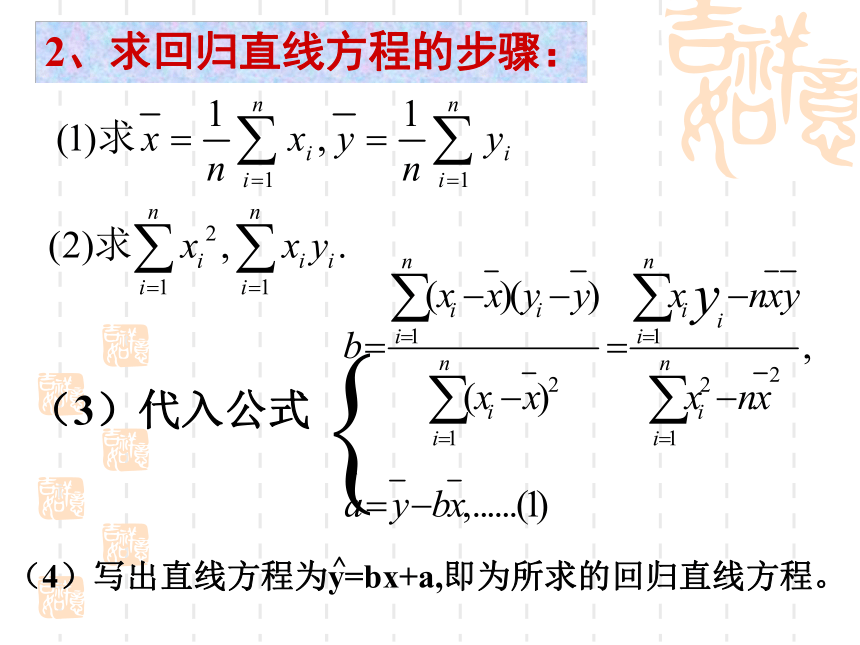
2、求回归直线方程的步骤:(3)代入公式典型例题 非 线性回归分析 小结:非线性回归分析的步骤将下列常见的非线性回归模型转化为线性回归模型。作变换得线形函数 . 1.幂函数:思考交流2. 指数曲线:作变换得线形函数 。 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费x1和年销售量y1(i=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值。
(1)根据散点图判断,y=a+bx与y=c+d 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;跟踪练习在实际问题中,有时很难说这些点是否存在一条直线附近,如上图。为了解决这个问题,我们对x与Y作线性相关性检验,简称相关性检验。思考交流?(1)假设两个随机变量的数据分别为则变量间线性相关系数r的计算公式如下:二、概念形成 相关性检验 (2)线性相关系数r及性性质:,其中 。线性相关性检验的步骤如下:1.做统计假设: x与Y不具有线性相关关系
2、根据小概率0.05与n-2在附表中查出r的一个临界值
3、根据样本相关系数计算公式算出r的值
4、做统计推断。如果|r|> ,表明有95%把握认为x与Y具有线性相关关系。
如果 我们说x与Y不具有线性相关关系,这时再求方程是毫无意义的。
例题2 为了了解某地母亲身高x与女儿身高Y的相关关系,随机测得10对母女的身高如下表所示:(1)画出散点图
(2)试对x与Y进行回归分析
(3)预测当母亲身高为161cm时女儿的身高为多少?例2 解:课堂小结3、 非线性回归方程: 对某些特殊的非线性关系,可以通过变换,将非
线性回归转化为线性回归,然后用线性回归的方法进
行研究,最后再转换为非线性回归方程。* 常见非线性回归模型:1.幂函数:2. 指数曲线:3、 对数曲线:1、 回归分析2、 相关系数:,其中 。1. 线性回归方程表示的直线必过( )
A.(0,0)点 B.(0,x)点 C.(0,y)点 D.点
2.对于相关系数,下列叙述正确的是( )
A. |r|越大,相关程度越高,反之相关程度越小
B. ||r|越小,相关程度越高,反之相关程度越小
C. |r|越接近1相关程度越高; |r|越接近0相关程度越小.
D.以上说法都不对.
3.设有一回归方程=2-1.5x,则变量增加一个单位时( )
A.平均增加1.5个单位 B. 平均增加2个单位
C. 平均减少1.5个单位 D. 平均减少2个单位当堂检测DCC祝同学们学习进步!!
教B版选修1-2学习目标
1、知道最小二乘法的思想,利用散点图分析两个变量是否存在相关关系,利用合适的回归模型求回归方程.
2、会用相关系数r,进行线性相关性检验问题1:正方形的面积y与正方形的边长x之间
的函数关系是y = x2问题2:在 7 块并排、形状大小相同的试验田上 进行施肥量对水稻产量影响的试验,得
到如下所示的一组数据:变量之间的两种关系 10 20 30 40 50500
450
400
350
300·······施化肥量水稻产量施化肥量x与水稻y具有的关系是相关关系是一种非确定的关系
现实生活中存在着大量的相关关系。
如:人的身高与年龄;
产品的成本与生产数量;
商品的销售额与广告费;
家庭的支出与收入等等对具有相关关系的两个变量进行统计分析的方法叫回归分析。10 20 30 40 50500
450
400
350
300·······发现:图中各点,大致分布在某条直线附近。散点图施化肥量水稻产量问题3:水稻产量y与施肥量x之间大致有何规律?
问题4:在这些点附近可画直线不止一条,哪条直线最能代表x与y之间的关系呢?
我们利用最小二乘法思想研究这个问题,通过最小二乘法得出求回归系数b和a的公式所求直线方程叫做回归直线方程;
2、求回归直线方程的步骤:(3)代入公式典型例题 非 线性回归分析 小结:非线性回归分析的步骤将下列常见的非线性回归模型转化为线性回归模型。作变换得线形函数 . 1.幂函数:思考交流2. 指数曲线:作变换得线形函数 。 某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费x1和年销售量y1(i=1,2,···,8)数据作了初步处理,得到下面的散点图及一些统计量的值。
(1)根据散点图判断,y=a+bx与y=c+d 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;跟踪练习在实际问题中,有时很难说这些点是否存在一条直线附近,如上图。为了解决这个问题,我们对x与Y作线性相关性检验,简称相关性检验。思考交流?(1)假设两个随机变量的数据分别为则变量间线性相关系数r的计算公式如下:二、概念形成 相关性检验 (2)线性相关系数r及性性质:,其中 。线性相关性检验的步骤如下:1.做统计假设: x与Y不具有线性相关关系
2、根据小概率0.05与n-2在附表中查出r的一个临界值
3、根据样本相关系数计算公式算出r的值
4、做统计推断。如果|r|> ,表明有95%把握认为x与Y具有线性相关关系。
如果 我们说x与Y不具有线性相关关系,这时再求方程是毫无意义的。
例题2 为了了解某地母亲身高x与女儿身高Y的相关关系,随机测得10对母女的身高如下表所示:(1)画出散点图
(2)试对x与Y进行回归分析
(3)预测当母亲身高为161cm时女儿的身高为多少?例2 解:课堂小结3、 非线性回归方程: 对某些特殊的非线性关系,可以通过变换,将非
线性回归转化为线性回归,然后用线性回归的方法进
行研究,最后再转换为非线性回归方程。* 常见非线性回归模型:1.幂函数:2. 指数曲线:3、 对数曲线:1、 回归分析2、 相关系数:,其中 。1. 线性回归方程表示的直线必过( )
A.(0,0)点 B.(0,x)点 C.(0,y)点 D.点
2.对于相关系数,下列叙述正确的是( )
A. |r|越大,相关程度越高,反之相关程度越小
B. ||r|越小,相关程度越高,反之相关程度越小
C. |r|越接近1相关程度越高; |r|越接近0相关程度越小.
D.以上说法都不对.
3.设有一回归方程=2-1.5x,则变量增加一个单位时( )
A.平均增加1.5个单位 B. 平均增加2个单位
C. 平均减少1.5个单位 D. 平均减少2个单位当堂检测DCC祝同学们学习进步!!
