2.1.2 演绎推理 课件(21张PPT)
文档属性
| 名称 | 2.1.2 演绎推理 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 415.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 00:00:00 | ||
图片预览






文档简介
课件21张PPT。2.2演绎推理学习目标
知识与技能:(1)了解演绎推理的含义,了解演绎推理三种不同的
推理规则
(2)能够用演绎推理三种不同的规则进行简单的推理
过程与方法:(1)通过对实例的分析、归纳总结的过程,培养自己
的理性思维能力.
(2)通过实例演练,体会演绎推理的推理思想,培养
良好的分析问题、 解决问题的能力.
情感态度价值观:通过本节课的学习,感受体会演绎推理三种推理
思想,感受演绎推理在数学及日常生活中的应用,
培养自己举一反三、以一知十、勇于探索、敢于
创新的精神.1. 由
1+3=4=22 ,
1+3+5=9=32 ,
1+3+5+7=16=42 ,
1+3+5+7+9=25=52 ,
……
猜想1+3+5+7+…+(2n-1)=归纳推理类比推理复习回顾 分析以下案例是合情推理吗?2. 平面内三条直线a,b,c
若a⊥c,b⊥c,则a∥b,类
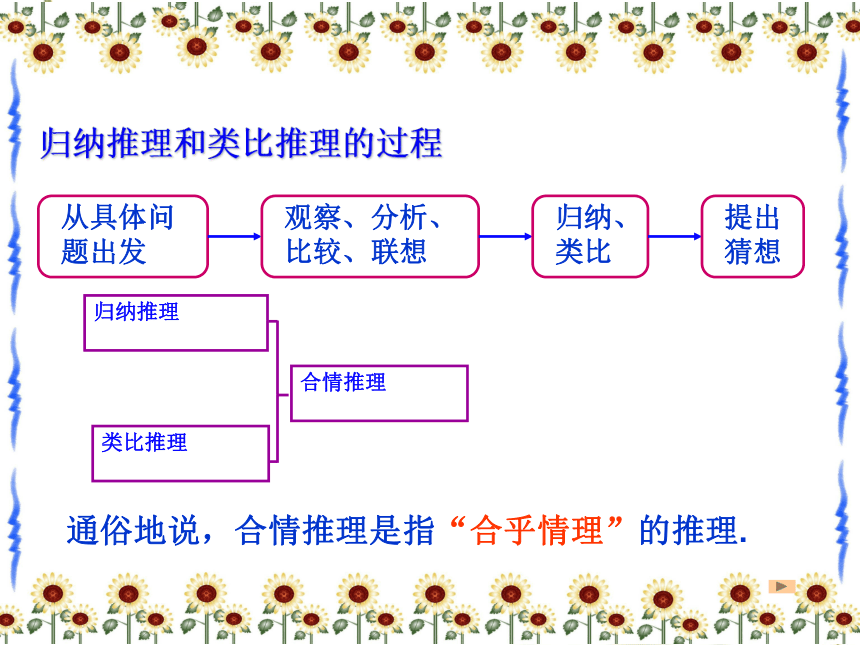
比推广到空间有三个平面若则∥归纳推理和类比推理的过程通俗地说,合情推理是指“合乎情理”的推理.新课引入:
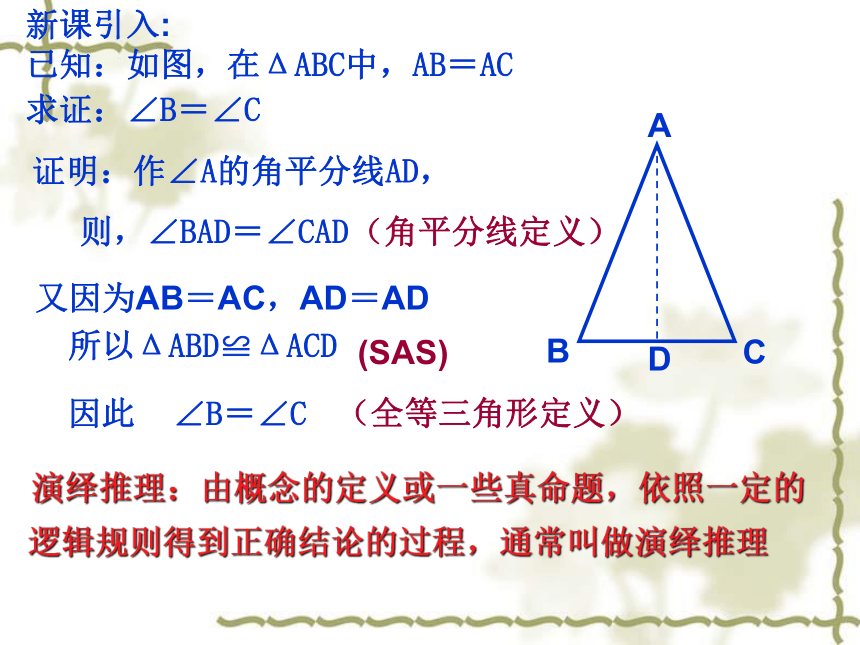
已知:如图,在ΔABC中,AB=AC求证:∠B=∠CABCD证明:作∠A的角平分线AD,则,∠BAD=∠CAD又因为AB=AC,AD=AD所以ΔABD≌ΔACD因此 ∠B=∠C演绎推理:由概念的定义或一些真命题,依照一定的逻辑规则得到正确结论的过程,通常叫做演绎推理(角平分线定义)(SAS)(全等三角形定义) 所有的平行四边形对角
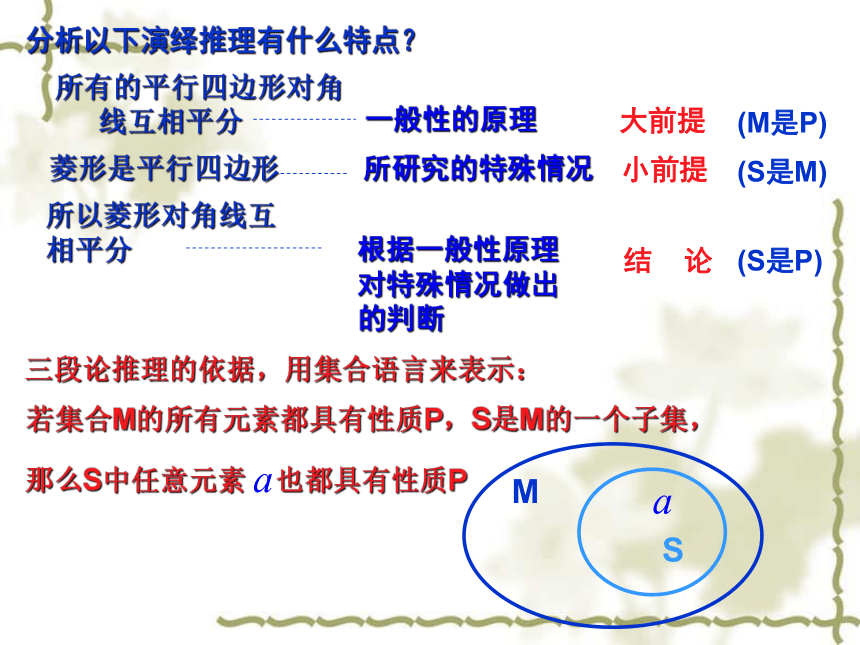
线互相平分 所以菱形对角线互相平分菱形是平行四边形 分析以下演绎推理有什么特点?大前提(M是P)小前提(S是M)结 论(S是P)三段论推理的依据,用集合语言来表示:用三段论的形式表示演绎推理 (1)在一个标准大气压下,水的沸点是100 ℃,所以在一个标准大气压下把水加热到100 ℃时,水会沸腾
(2)一切奇数都不能被2整除,2100+1是奇数,所以2100+1不能被2整除;
(3)三角函数都是周期函数,y=tan α是三角函数,因此y=tan α是周期函数.
(4)一次函数是单调函数,函数y=2x-1是一次函数,所以y=2x-1是单调函数;
(5)等差数列的通项公式具有形式an=pn+q(p,q是常数),数列1,2,3,…,n是等差数列,所以数列1,2,3,…,n的通项具有an=pn+q的形式.
应用例1. 分析下列推理是否正确,为什么?(1)自然数是整数3是自然数3是整数(2)自然数是整数-3是整数-3是自然数(3)自然数是整数-3是自然数-3是整数推理形式错误小前提错误√╳╳因为指数函数 是增函数,·······大前提而 是指数函数, ···········小前提所以 是增函数。············结论(1)上面的推理形式正确吗?
(2)推理的结论正确吗?为什么? 上述推理的形式是正确,但大前提是错误的(因为指数函数y =ax (0①大前提错误;
②小前提错误;
③推理形式错误正确的前提和推理形式一定能得到正确的结论!☆但是所以,我们主要运用演绎推理来证明数学命题(小前提不成立或不符合大前提的条件)(大前提不成立)因而,演绎推理可以作为数学中严格证明的工具练习 已知:空间四边形中,
点E,F分别是AB,AD的中点,
求证:EF//平面BCD证明:连接BD,因为点E,F分别是AB,AD的中点
所以,EF//BD
AEBCDF省略大前提:三角形的中位线平行于第三边省略大前提:如果平面外一条直线和这个平面内的一条直线
平行,那么这条直线和这个平面平行又因为,EF 平面BCD,BD 平面BCD
所以 EF//平面BCD
规律方法用三段论写推理过程时,关键是明确大、小前提,三段论中的大前提提供了一个一般性的原理,小前提指出了一种特殊情况,两个命题结合起来,揭示了一般原理与特殊情况的内在联系.有时可省略小前提,有时甚至也可大前提与小前提都省略.在寻找大前提时,可找一个使结论成立的充分条件作为大前提.
例3 求证:当a>1时,有:关键步骤是(1)
(2)
所以,原式成立。这里用到的推理规则是“如果aRb, bRc, 则 aRc”,
其中 “R” 表示具有传递性的关系。这种推理规则
叫做传递性关系推理
例4 证明函数 证明:像这种把所有情况都考虑在内的演绎推理规则叫做完全归纳推理 的值恒为正数1、下列推理的两个步骤分别遵循哪种推理规则?
因为AB//CD,
所以
又因为
所以∠1= ∠3∠2= ∠3∠1= ∠2312练习三段论 传递性关系推理ABCD2、在证明圆周角度数定理时,我们考虑:
(1)圆心在圆周角的一边上;
(2)圆心在圆周角内;
(3)圆心在圆周角外;
三种情况,而推得圆周角定理。ABCOABCOOABC上面的推理遵循哪种推理规则?合情推理与演绎推理的区别合情推理归纳推理类比推理由部分到整体,个别到一般的推理由特殊到特殊的推理结论不一定正确,有待进一
步证明,重在发现。演绎推理由一般到特殊的
推理前提和推理形式都正确时,结论一定正确,重在证明 合情推理的结论需要演绎推理的验证,而演绎推理的方向和思路一般是通过合情推理获得的 小 结
1.方面知识 推 理 演绎推理 合情推理 三 段 论传递性关系推理 完全归纳推理 归 纳 推 理 类 比 推 理2.数学核心素养:1.数学抽象:从事物的具体背景中抽象出一般规律和结构。
2逻辑推理:从特殊到一般的推理和从特殊到特殊,从一般到特殊的推理方法。作 业 课本第34页 练习A组第1、2题课本第35页 习题2-1B组第2题谢 谢
推理规则
(2)能够用演绎推理三种不同的规则进行简单的推理
过程与方法:(1)通过对实例的分析、归纳总结的过程,培养自己
的理性思维能力.
(2)通过实例演练,体会演绎推理的推理思想,培养
良好的分析问题、 解决问题的能力.
情感态度价值观:通过本节课的学习,感受体会演绎推理三种推理
思想,感受演绎推理在数学及日常生活中的应用,
培养自己举一反三、以一知十、勇于探索、敢于
创新的精神.1. 由
1+3=4=22 ,
1+3+5=9=32 ,
1+3+5+7=16=42 ,
1+3+5+7+9=25=52 ,
……
猜想1+3+5+7+…+(2n-1)=归纳推理类比推理复习回顾 分析以下案例是合情推理吗?2. 平面内三条直线a,b,c
若a⊥c,b⊥c,则a∥b,类
比推广到空间有三个平面若则∥归纳推理和类比推理的过程通俗地说,合情推理是指“合乎情理”的推理.新课引入:
已知:如图,在ΔABC中,AB=AC求证:∠B=∠CABCD证明:作∠A的角平分线AD,则,∠BAD=∠CAD又因为AB=AC,AD=AD所以ΔABD≌ΔACD因此 ∠B=∠C演绎推理:由概念的定义或一些真命题,依照一定的逻辑规则得到正确结论的过程,通常叫做演绎推理(角平分线定义)(SAS)(全等三角形定义) 所有的平行四边形对角
线互相平分 所以菱形对角线互相平分菱形是平行四边形 分析以下演绎推理有什么特点?大前提(M是P)小前提(S是M)结 论(S是P)三段论推理的依据,用集合语言来表示:用三段论的形式表示演绎推理 (1)在一个标准大气压下,水的沸点是100 ℃,所以在一个标准大气压下把水加热到100 ℃时,水会沸腾
(2)一切奇数都不能被2整除,2100+1是奇数,所以2100+1不能被2整除;
(3)三角函数都是周期函数,y=tan α是三角函数,因此y=tan α是周期函数.
(4)一次函数是单调函数,函数y=2x-1是一次函数,所以y=2x-1是单调函数;
(5)等差数列的通项公式具有形式an=pn+q(p,q是常数),数列1,2,3,…,n是等差数列,所以数列1,2,3,…,n的通项具有an=pn+q的形式.
应用例1. 分析下列推理是否正确,为什么?(1)自然数是整数3是自然数3是整数(2)自然数是整数-3是整数-3是自然数(3)自然数是整数-3是自然数-3是整数推理形式错误小前提错误√╳╳因为指数函数 是增函数,·······大前提而 是指数函数, ···········小前提所以 是增函数。············结论(1)上面的推理形式正确吗?
(2)推理的结论正确吗?为什么? 上述推理的形式是正确,但大前提是错误的(因为指数函数y =ax (0
②小前提错误;
③推理形式错误正确的前提和推理形式一定能得到正确的结论!☆但是所以,我们主要运用演绎推理来证明数学命题(小前提不成立或不符合大前提的条件)(大前提不成立)因而,演绎推理可以作为数学中严格证明的工具练习 已知:空间四边形中,
点E,F分别是AB,AD的中点,
求证:EF//平面BCD证明:连接BD,因为点E,F分别是AB,AD的中点
所以,EF//BD
AEBCDF省略大前提:三角形的中位线平行于第三边省略大前提:如果平面外一条直线和这个平面内的一条直线
平行,那么这条直线和这个平面平行又因为,EF 平面BCD,BD 平面BCD
所以 EF//平面BCD
规律方法用三段论写推理过程时,关键是明确大、小前提,三段论中的大前提提供了一个一般性的原理,小前提指出了一种特殊情况,两个命题结合起来,揭示了一般原理与特殊情况的内在联系.有时可省略小前提,有时甚至也可大前提与小前提都省略.在寻找大前提时,可找一个使结论成立的充分条件作为大前提.
例3 求证:当a>1时,有:关键步骤是(1)
(2)
所以,原式成立。这里用到的推理规则是“如果aRb, bRc, 则 aRc”,
其中 “R” 表示具有传递性的关系。这种推理规则
叫做传递性关系推理
例4 证明函数 证明:像这种把所有情况都考虑在内的演绎推理规则叫做完全归纳推理 的值恒为正数1、下列推理的两个步骤分别遵循哪种推理规则?
因为AB//CD,
所以
又因为
所以∠1= ∠3∠2= ∠3∠1= ∠2312练习三段论 传递性关系推理ABCD2、在证明圆周角度数定理时,我们考虑:
(1)圆心在圆周角的一边上;
(2)圆心在圆周角内;
(3)圆心在圆周角外;
三种情况,而推得圆周角定理。ABCOABCOOABC上面的推理遵循哪种推理规则?合情推理与演绎推理的区别合情推理归纳推理类比推理由部分到整体,个别到一般的推理由特殊到特殊的推理结论不一定正确,有待进一
步证明,重在发现。演绎推理由一般到特殊的
推理前提和推理形式都正确时,结论一定正确,重在证明 合情推理的结论需要演绎推理的验证,而演绎推理的方向和思路一般是通过合情推理获得的 小 结
1.方面知识 推 理 演绎推理 合情推理 三 段 论传递性关系推理 完全归纳推理 归 纳 推 理 类 比 推 理2.数学核心素养:1.数学抽象:从事物的具体背景中抽象出一般规律和结构。
2逻辑推理:从特殊到一般的推理和从特殊到特殊,从一般到特殊的推理方法。作 业 课本第34页 练习A组第1、2题课本第35页 习题2-1B组第2题谢 谢
