3.2 空间向量在立体几何中的应用 课件(31张PPT)
文档属性
| 名称 | 3.2 空间向量在立体几何中的应用 课件(31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 584.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 19:38:17 | ||
图片预览









文档简介
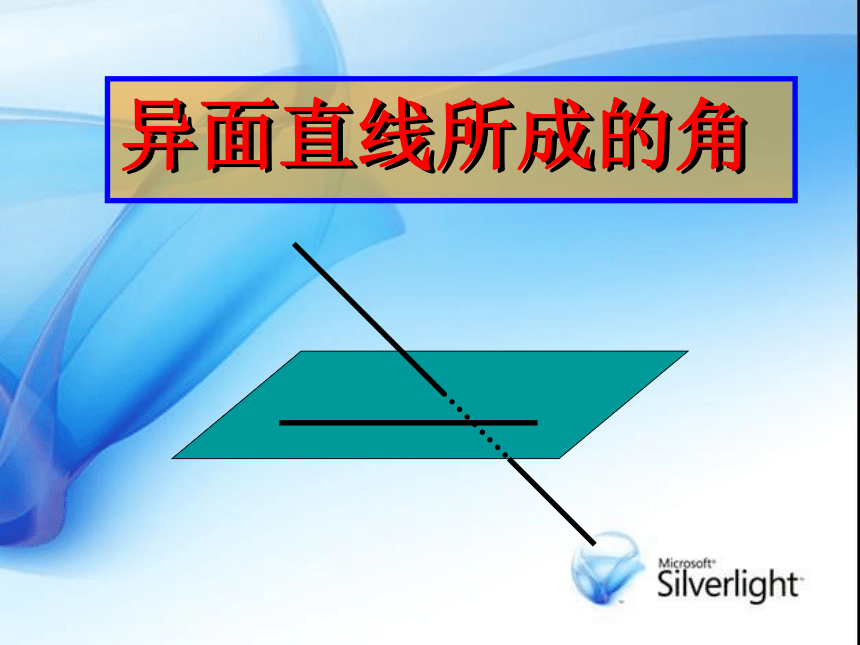
课件31张PPT。用向量法求空间角立体几何中的向量方法空间的角直线与平面所成角直线与平面所成角平面与平面所成角平面与平面所成角1.空间角及向量求法|cos〈a,b〉|例1如图在正方体ABCD-A1B1C1D1中,M是AB的中点,则对角线DB1与CM所成角的余弦值为_____. zyB1C1D1A1CDA BCD解: 以A为原点建立如图所示的直角坐标系A- xyz, 设正方体的棱长为2,则
M(1,0, 0),C(2,2,0), B1(2, 0, 2),D(0,2 ,0),
于是,
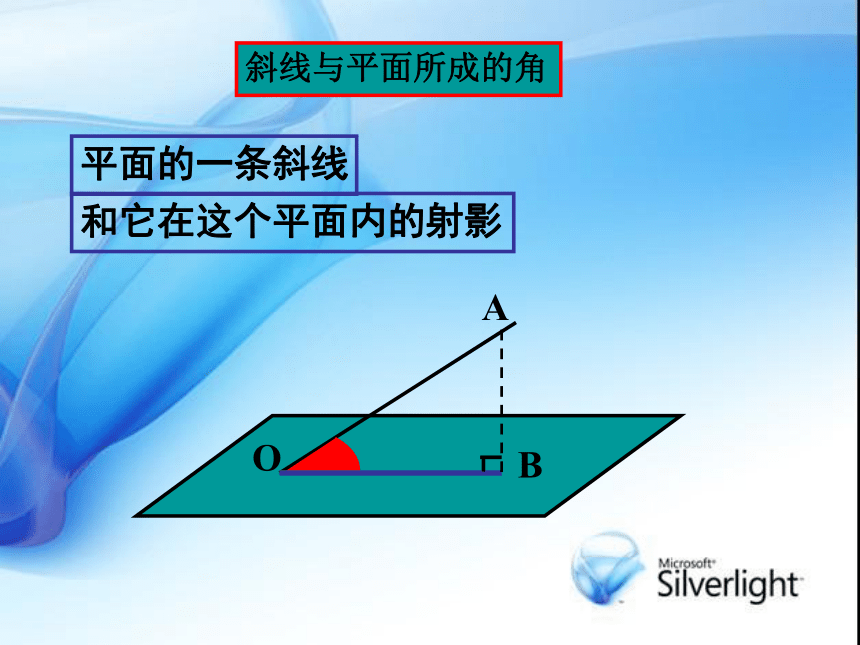
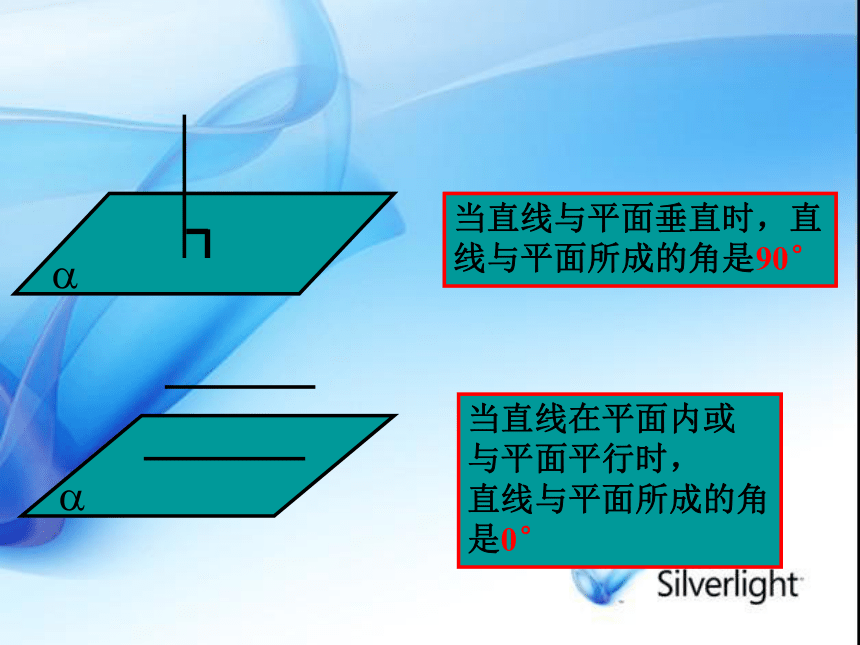
∴cos< , >=链接高考答案:A线面角斜线与平面所成的角平面的一条斜线和它在这个平面内的射影当直线与平面垂直时,直
线与平面所成的角是90°当直线在平面内或
与平面平行时,
直线与平面所成的角是0°|cos〈a,n〉|步骤:例2:正三棱柱ABC-A1B1C1的底面边长为1,高为 ,求AC1与侧面ABB1A1所成的角zxyC1A1B1ACBO解:建立如图示的直角坐标系,则
A( ,0,0),B(0, ,0) A1( ,0, ). C(- ,0, 0 )
设面ABB1A1的法向量为n=(x,y,z)
由 得
取y= ,得n=(3, ,0)
而
∴
∴C1A1B1CAOBxyz二面角从一条直线出发的两个半平面所形成的图形叫做二面角这条直线叫做二面角的棱从一条直线出发的两个半平面所形成的图形叫做二面角这条直线叫做二面角的棱以二面角的棱上任意一点为端点,以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角(3)二面角
设n1 、n2分别是二面角两个半平面α、β的法向量,由几何知识可知,二面角α-L-β的大小与法向量n1 、n2夹角相等(选取法向量竖坐标z同号时相等)或互补(选取法向量竖坐标z异号时互补),于是求二面角的大小可转化为求两个平面法向量的夹角,这样可避免了二面角的平面角的作图麻烦.n1|cos〈n1,n2〉|例3:在四棱锥S-ABCD中∠DAB=∠ABC=90°,侧棱SA⊥底面AC,SA=AB=BC=1,AD=2,求二面角A-SD-C的大小.解:建立如图所示的空间直角坐标系O-xyz,则 B(1,0,0),C(1,1,0),D(0,2,0),S(0,0,1).
设平面SCD的法向量n1=(x,y,z),则由
得
n1=(1,1,2).
而面SAD的法向量n2 = (1,0,0).
于是二面角A-SD-C的大小θ满足
∴二面角A-SD-C的大小为 .链接高考aba′b′?oaba′b′o?课堂小结1.异面直线所成角: 2.直线与平面所成角: 3.二面角:作业布置:见学案谢谢!再见
M(1,0, 0),C(2,2,0), B1(2, 0, 2),D(0,2 ,0),
于是,
∴cos< , >=链接高考答案:A线面角斜线与平面所成的角平面的一条斜线和它在这个平面内的射影当直线与平面垂直时,直
线与平面所成的角是90°当直线在平面内或
与平面平行时,
直线与平面所成的角是0°|cos〈a,n〉|步骤:例2:正三棱柱ABC-A1B1C1的底面边长为1,高为 ,求AC1与侧面ABB1A1所成的角zxyC1A1B1ACBO解:建立如图示的直角坐标系,则
A( ,0,0),B(0, ,0) A1( ,0, ). C(- ,0, 0 )
设面ABB1A1的法向量为n=(x,y,z)
由 得
取y= ,得n=(3, ,0)
而
∴
∴C1A1B1CAOBxyz二面角从一条直线出发的两个半平面所形成的图形叫做二面角这条直线叫做二面角的棱从一条直线出发的两个半平面所形成的图形叫做二面角这条直线叫做二面角的棱以二面角的棱上任意一点为端点,以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角(3)二面角
设n1 、n2分别是二面角两个半平面α、β的法向量,由几何知识可知,二面角α-L-β的大小与法向量n1 、n2夹角相等(选取法向量竖坐标z同号时相等)或互补(选取法向量竖坐标z异号时互补),于是求二面角的大小可转化为求两个平面法向量的夹角,这样可避免了二面角的平面角的作图麻烦.n1|cos〈n1,n2〉|例3:在四棱锥S-ABCD中∠DAB=∠ABC=90°,侧棱SA⊥底面AC,SA=AB=BC=1,AD=2,求二面角A-SD-C的大小.解:建立如图所示的空间直角坐标系O-xyz,则 B(1,0,0),C(1,1,0),D(0,2,0),S(0,0,1).
设平面SCD的法向量n1=(x,y,z),则由
得
n1=(1,1,2).
而面SAD的法向量n2 = (1,0,0).
于是二面角A-SD-C的大小θ满足
∴二面角A-SD-C的大小为 .链接高考aba′b′?oaba′b′o?课堂小结1.异面直线所成角: 2.直线与平面所成角: 3.二面角:作业布置:见学案谢谢!再见
