3.2.4 二面角及其度量 课件(37张PPT)
文档属性
| 名称 | 3.2.4 二面角及其度量 课件(37张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 265.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 19:39:26 | ||
图片预览




文档简介
课件37张PPT。2.3.2线面角、二面角一、温习故知1、定义:2、性质:3、判定定理:C错
错
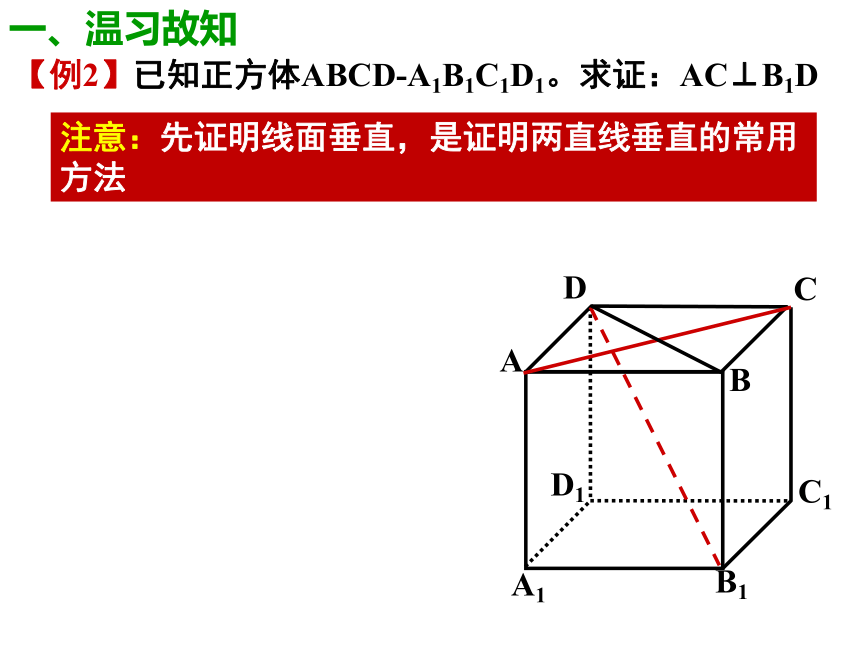
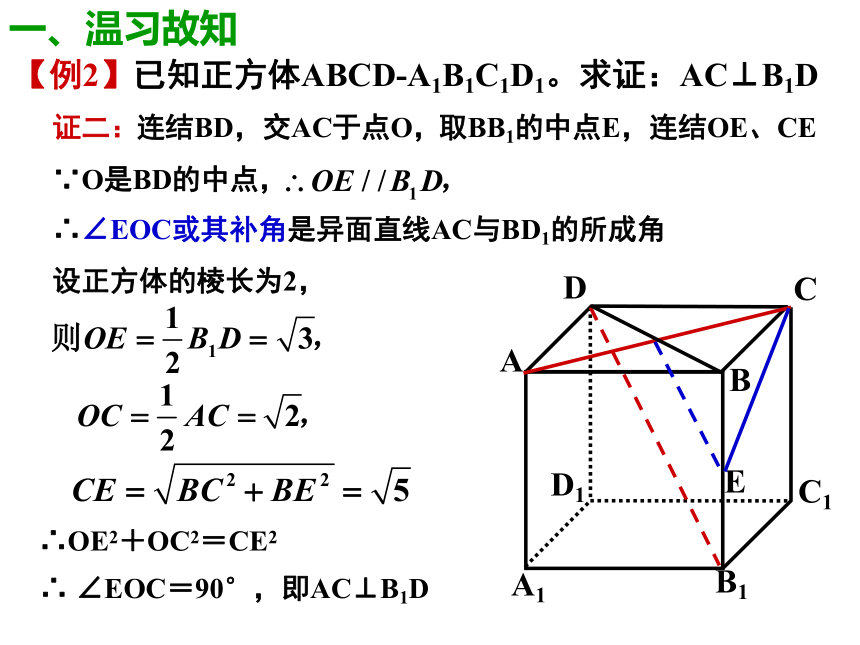
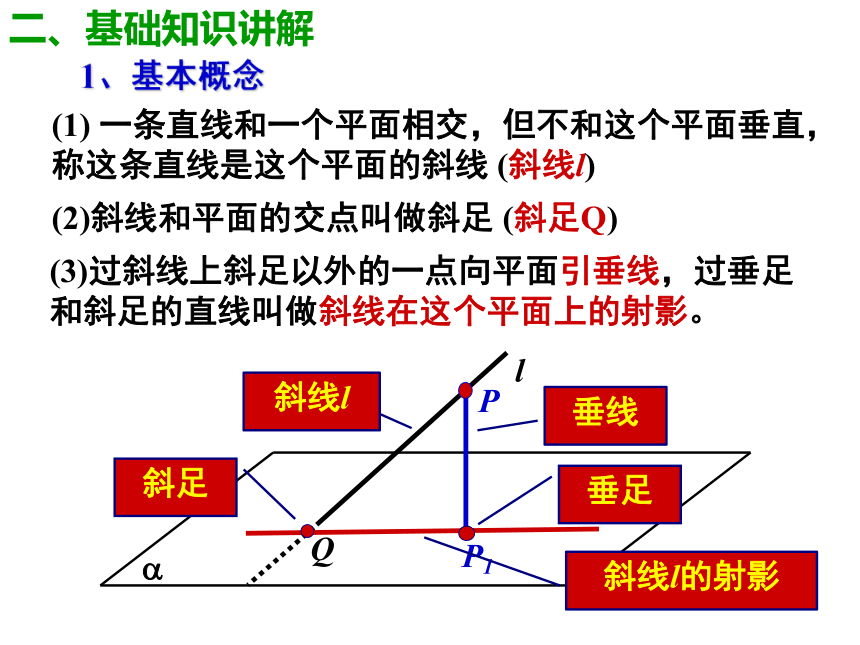
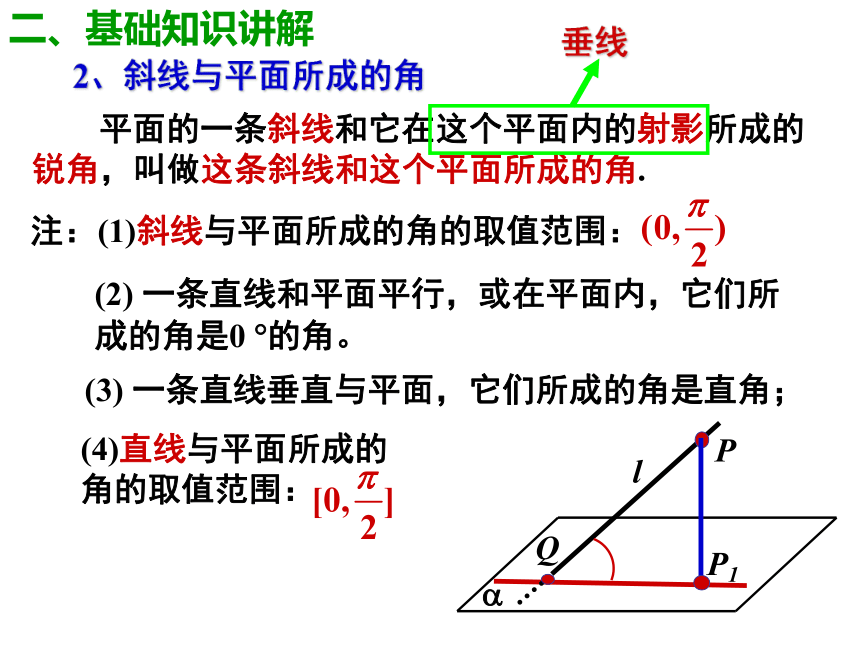
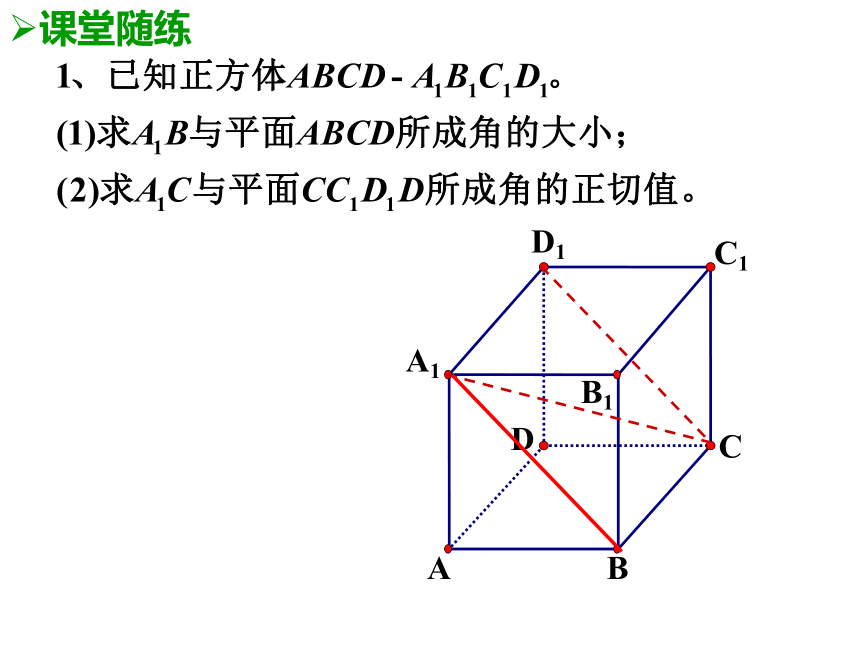
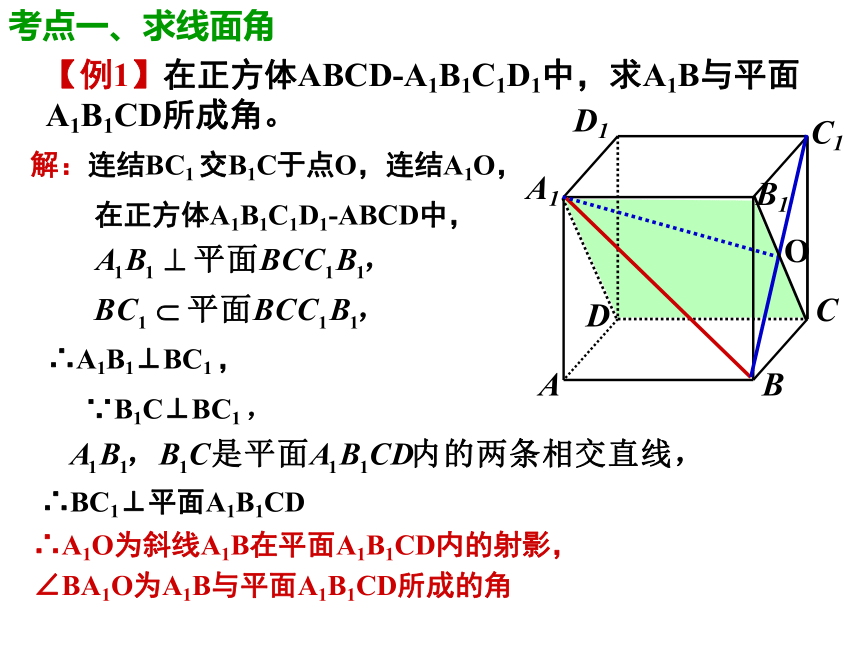
对一、温习故知【例2】已知正方体ABCD-A1B1C1D1。求证:AC⊥B1D注意:先证明线面垂直,是证明两直线垂直的常用方法一、温习故知【例2】已知正方体ABCD-A1B1C1D1。求证:AC⊥B1D证二:E连结BD,交AC于点O,取BB1的中点E,连结OE、CE∵O是BD的中点,∴∠EOC或其补角是异面直线AC与BD1的所成角设正方体的棱长为2,∴OE2+OC2=CE2∴ ∠EOC=90°,即AC⊥B1D一、温习故知(1) 一条直线和一个平面相交,但不和这个平面垂直,称这条直线是这个平面的斜线 (斜线l)(2)斜线和平面的交点叫做斜足 (斜足Q)(3)过斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面上的射影。1、基本概念斜线l斜线l的射影垂线斜足垂足二、基础知识讲解2、斜线与平面所成的角 平面的一条斜线和它在这个平面内的射影所成的锐角,叫做这条斜线和这个平面所成的角.注:(1)斜线与平面所成的角的取值范围:(2) 一条直线和平面平行,或在平面内,它们所成的角是0 ?的角。(3) 一条直线垂直与平面,它们所成的角是直角;(4)直线与平面所成的角的取值范围:二、基础知识讲解垂线D1C1B1A1DCBA课堂随练【例1】在正方体ABCD-A1B1C1D1中,求A1B与平面A1B1CD所成角。解:连结BC1 交B1C于点O,连结A1O,∴A1B1⊥BC1 ,∵B1C⊥BC1 ,∴BC1⊥平面A1B1CD∴A1O为斜线A1B在平面A1B1CD内的射影,
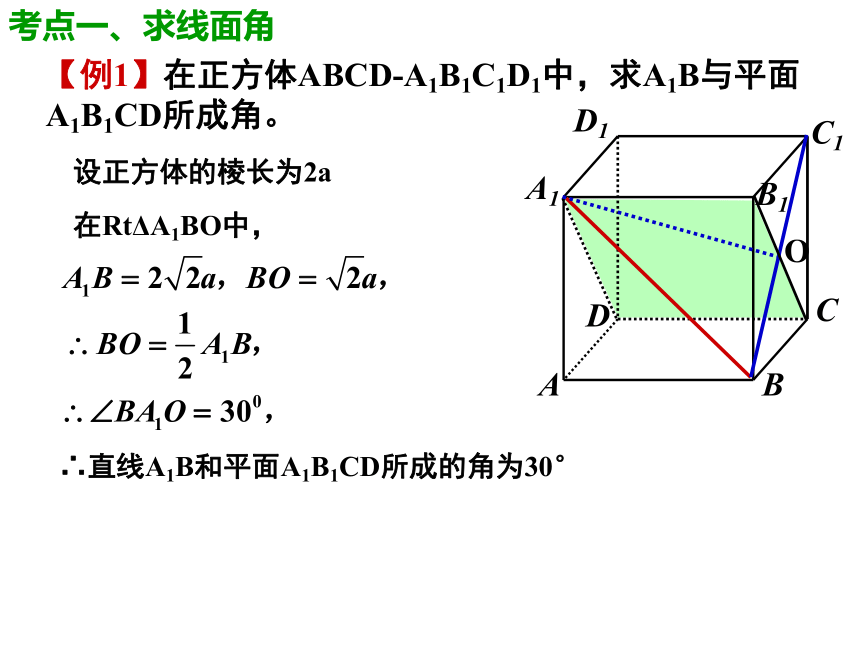
∠BA1O为A1B与平面A1B1CD所成的角在正方体A1B1C1D1-ABCD中,考点一、求线面角【例1】在正方体ABCD-A1B1C1D1中,求A1B与平面A1B1CD所成角。设正方体的棱长为2a在RtΔA1BO中,∴直线A1B和平面A1B1CD所成的角为30°考点一、求线面角解:连结BC1 交B1C于点O,连结A1O,∴A1B1⊥BC1 ,∵B1C⊥BC1 ,∴BC1⊥平面A1B1CD∴A1O为斜线A1B在平面A1B1CD内的射影,
∠BA1O为A1B与平面A1B1CD所成的角在正方体A1B1C1D1-ABCD中,设正方体的棱长为2a,在RtΔA1BO中,∴直线A1B和平面A1B1CD所成的角为30°一“作”二“证”三“计算”四“下结论”课堂随练一、温习故知 一个平面内的一条直线把这个平面分成两个部分,其中的每一部分都叫做半平面。 一条直线上的一个点把这条直线分成两个部分,其中的每一部分都叫做射线。【思考】在平面几何中“射线”是怎样定义的?1、半平面2、请把书打开点,是指哪个比较大?【问题2】我们怎么去度量两个平面的相对位置关系呢?1、请把门开大点,是指哪个比较大?二、创设情境【问题1】αβBAl 这条直线叫做二面角的棱,这两个半平面叫做二面角的面。 如图,从一条直线出发的两个半平面所组成的图形叫做二面角。三、基础知识讲解2、二面角 棱AB、面分别为α,β的二面角记作二面角α-AB-β。
也可在α,β内(棱以外的半平面的部分)分别取点P,Q将这个二面角记作二面角P-AB-Q. 如果棱记作l,那么这个二面角记作二面角α-l-β或P-l-Q.3、二面角的画法:(1)平卧式(2)直立式二面角C-AB- D二面角?-AB- ?二面角?- l- ?二面角C-AB- D∠AOB4、二面角的表示方法二面角定义与平面角定义的对比从一条直线出发的两个半平面所组成的图形叫做二面角面—直线(棱) —面二面角?—l—?或二面角?—AB—?定义构成表示法图形从一点出发的两条射线所组成的图形叫做平面角。边—点—边
(顶点)∠AOB图形定义图形平面角二面角5、二面角的平面角: 以二面角的棱上任意一点为端点,在两个面上分别引垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。?等角定理:如果一个角的两边和另
一个角的两边分别平行,并且方向相
同,那么这两个角相等。注:(1)二面角的平面角与顶点在棱上的位置无关,只与二面角的张角大小有关。
(2)二面角是用它的平面角来度量的,一个二面角的平面角多大,就说这个二面角是多少度的二面角。注意二面角的平面角必须满足:(1)(2)(3)二面角的范围:(4)直二面角—— 平面角为直角的二面角叫做直二面角当二面角的两个面合成一个平面时,规定为180o。
当二面角的两个面重合时,规定为0o。
因此,二面角大小的范围为[0,π]。【思考】如图,点A在二面角α-l-β的半平面α上一点,过点A如何确定二面角α-l-β的平面角?OB??lA——“定义法”6、二面角的平面角的作法:----“三垂线法”过点A作AB⊥平面β交于点B ,过点A作AO⊥直线 l 交于O,【思考】如图,点A在二面角α-l-β的半平面α上一点,过点A如何确定二面角α-l-β的平面角?4、二面角的平面角的作法:连结OB ,则∠AOB为所求的角C D解:在AB上取不同于P 的一点O,在?内过O作OC⊥AB交PM 于C,在 ? 内作OD⊥AB交PN于D,连结CD,设PO = a ,∵∠BPM =∠BPN = 45o又∵∠MPN=60o ∴∠COD=90o因此,此二面角的度数为90o【例1】如图,已知P是二面角α-AB -β棱上一点,过P 分别在?、?内引射线PM、PN,且∠MPN=600,∠BPM =∠BPN =450,求此二面角的度数。则∠COD是二面角α-AB-β的平面角一“作”
二“证”
三“计算”
四“下结论”考点二、求二面角ABCDVOE五、针对性练习1、线面角、二面角的定义2、二面角平面角的作法
(1)定义法
(2)垂面法
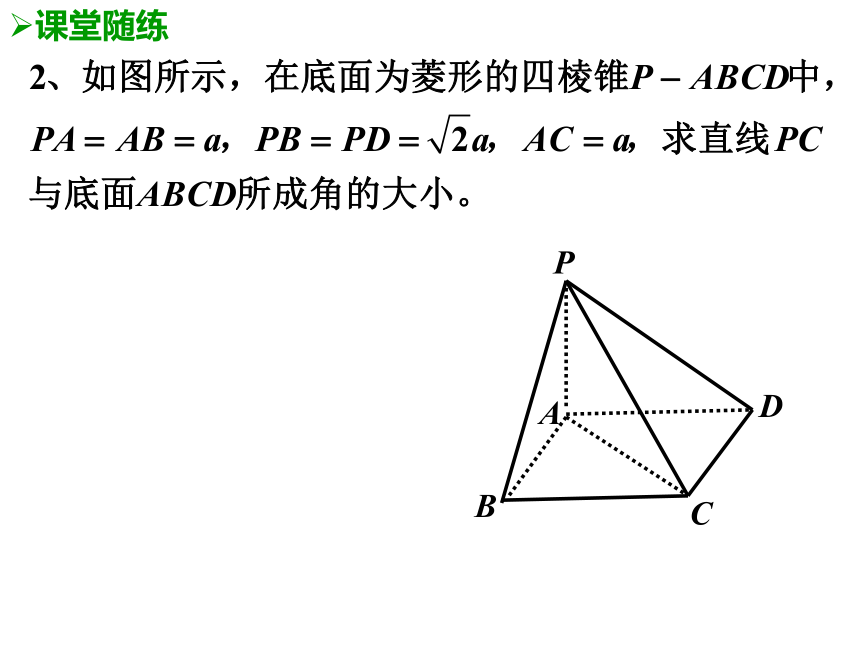
(3)三垂线法3、空间角的求解步骤一“作”二“证”三“计算”四“下结论”六、课时小结七、布置作业课本P73 习题2.3 A组第4题VDBAC三、作业讲解MACB四、针对性练习AOBCα三、典例分析OM四、针对性练习1、斜线与平面所成的角五、课时小结解题步骤:1)找(作)线面垂直,寻找线面角;2)求证、确定线面角;3)解三角形,求角。4)下结论。1、已知三棱锥P-ABC的三条侧棱PA=PB=PC,
PO ⊥平面ABC,则点O是△ABC的_____心外OA=OB=OCPABCO中四、针对性练习2、已知三棱锥P-ABC的顶点P到底面三角形ABC的三条边的距离相等,PO ⊥平面ABC,则点O是△ABC的_____心PABCOEF内PA=PB=PCOA=OB=OCPE=PF=PGGOE=OF=OG3、已知三棱锥P-ABC的三条侧棱PA,PB,PC两两垂直,PO ⊥平面ABC,则点O是△ABC的_____心PABCDO垂四、针对性练习PABCODFAOD 例2、已知锐二面角?- l- ? ,A为面?内一点,A到? 的距离为 ,到 l 的距离为 4,求二面角 ?- l- ? 的大小。解:过 A作 AO⊥ ?于O,过 O作 OD⊥ l 于D,连AD∴AO= 2 ,AD=4∵ AO为 A到?的距离 , AD为 A到 l 的距离∴∠ADO就是二面角 ?- l- ? 的平面角∴ ∠ADO=60°∴二面角 ?- l- ? 的大小为60 °在R t △AOD中,∵sin∠ADO=
错
对一、温习故知【例2】已知正方体ABCD-A1B1C1D1。求证:AC⊥B1D注意:先证明线面垂直,是证明两直线垂直的常用方法一、温习故知【例2】已知正方体ABCD-A1B1C1D1。求证:AC⊥B1D证二:E连结BD,交AC于点O,取BB1的中点E,连结OE、CE∵O是BD的中点,∴∠EOC或其补角是异面直线AC与BD1的所成角设正方体的棱长为2,∴OE2+OC2=CE2∴ ∠EOC=90°,即AC⊥B1D一、温习故知(1) 一条直线和一个平面相交,但不和这个平面垂直,称这条直线是这个平面的斜线 (斜线l)(2)斜线和平面的交点叫做斜足 (斜足Q)(3)过斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面上的射影。1、基本概念斜线l斜线l的射影垂线斜足垂足二、基础知识讲解2、斜线与平面所成的角 平面的一条斜线和它在这个平面内的射影所成的锐角,叫做这条斜线和这个平面所成的角.注:(1)斜线与平面所成的角的取值范围:(2) 一条直线和平面平行,或在平面内,它们所成的角是0 ?的角。(3) 一条直线垂直与平面,它们所成的角是直角;(4)直线与平面所成的角的取值范围:二、基础知识讲解垂线D1C1B1A1DCBA课堂随练【例1】在正方体ABCD-A1B1C1D1中,求A1B与平面A1B1CD所成角。解:连结BC1 交B1C于点O,连结A1O,∴A1B1⊥BC1 ,∵B1C⊥BC1 ,∴BC1⊥平面A1B1CD∴A1O为斜线A1B在平面A1B1CD内的射影,
∠BA1O为A1B与平面A1B1CD所成的角在正方体A1B1C1D1-ABCD中,考点一、求线面角【例1】在正方体ABCD-A1B1C1D1中,求A1B与平面A1B1CD所成角。设正方体的棱长为2a在RtΔA1BO中,∴直线A1B和平面A1B1CD所成的角为30°考点一、求线面角解:连结BC1 交B1C于点O,连结A1O,∴A1B1⊥BC1 ,∵B1C⊥BC1 ,∴BC1⊥平面A1B1CD∴A1O为斜线A1B在平面A1B1CD内的射影,
∠BA1O为A1B与平面A1B1CD所成的角在正方体A1B1C1D1-ABCD中,设正方体的棱长为2a,在RtΔA1BO中,∴直线A1B和平面A1B1CD所成的角为30°一“作”二“证”三“计算”四“下结论”课堂随练一、温习故知 一个平面内的一条直线把这个平面分成两个部分,其中的每一部分都叫做半平面。 一条直线上的一个点把这条直线分成两个部分,其中的每一部分都叫做射线。【思考】在平面几何中“射线”是怎样定义的?1、半平面2、请把书打开点,是指哪个比较大?【问题2】我们怎么去度量两个平面的相对位置关系呢?1、请把门开大点,是指哪个比较大?二、创设情境【问题1】αβBAl 这条直线叫做二面角的棱,这两个半平面叫做二面角的面。 如图,从一条直线出发的两个半平面所组成的图形叫做二面角。三、基础知识讲解2、二面角 棱AB、面分别为α,β的二面角记作二面角α-AB-β。
也可在α,β内(棱以外的半平面的部分)分别取点P,Q将这个二面角记作二面角P-AB-Q. 如果棱记作l,那么这个二面角记作二面角α-l-β或P-l-Q.3、二面角的画法:(1)平卧式(2)直立式二面角C-AB- D二面角?-AB- ?二面角?- l- ?二面角C-AB- D∠AOB4、二面角的表示方法二面角定义与平面角定义的对比从一条直线出发的两个半平面所组成的图形叫做二面角面—直线(棱) —面二面角?—l—?或二面角?—AB—?定义构成表示法图形从一点出发的两条射线所组成的图形叫做平面角。边—点—边
(顶点)∠AOB图形定义图形平面角二面角5、二面角的平面角: 以二面角的棱上任意一点为端点,在两个面上分别引垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。?等角定理:如果一个角的两边和另
一个角的两边分别平行,并且方向相
同,那么这两个角相等。注:(1)二面角的平面角与顶点在棱上的位置无关,只与二面角的张角大小有关。
(2)二面角是用它的平面角来度量的,一个二面角的平面角多大,就说这个二面角是多少度的二面角。注意二面角的平面角必须满足:(1)(2)(3)二面角的范围:(4)直二面角—— 平面角为直角的二面角叫做直二面角当二面角的两个面合成一个平面时,规定为180o。
当二面角的两个面重合时,规定为0o。
因此,二面角大小的范围为[0,π]。【思考】如图,点A在二面角α-l-β的半平面α上一点,过点A如何确定二面角α-l-β的平面角?OB??lA——“定义法”6、二面角的平面角的作法:----“三垂线法”过点A作AB⊥平面β交于点B ,过点A作AO⊥直线 l 交于O,【思考】如图,点A在二面角α-l-β的半平面α上一点,过点A如何确定二面角α-l-β的平面角?4、二面角的平面角的作法:连结OB ,则∠AOB为所求的角C D解:在AB上取不同于P 的一点O,在?内过O作OC⊥AB交PM 于C,在 ? 内作OD⊥AB交PN于D,连结CD,设PO = a ,∵∠BPM =∠BPN = 45o又∵∠MPN=60o ∴∠COD=90o因此,此二面角的度数为90o【例1】如图,已知P是二面角α-AB -β棱上一点,过P 分别在?、?内引射线PM、PN,且∠MPN=600,∠BPM =∠BPN =450,求此二面角的度数。则∠COD是二面角α-AB-β的平面角一“作”
二“证”
三“计算”
四“下结论”考点二、求二面角ABCDVOE五、针对性练习1、线面角、二面角的定义2、二面角平面角的作法
(1)定义法
(2)垂面法
(3)三垂线法3、空间角的求解步骤一“作”二“证”三“计算”四“下结论”六、课时小结七、布置作业课本P73 习题2.3 A组第4题VDBAC三、作业讲解MACB四、针对性练习AOBCα三、典例分析OM四、针对性练习1、斜线与平面所成的角五、课时小结解题步骤:1)找(作)线面垂直,寻找线面角;2)求证、确定线面角;3)解三角形,求角。4)下结论。1、已知三棱锥P-ABC的三条侧棱PA=PB=PC,
PO ⊥平面ABC,则点O是△ABC的_____心外OA=OB=OCPABCO中四、针对性练习2、已知三棱锥P-ABC的顶点P到底面三角形ABC的三条边的距离相等,PO ⊥平面ABC,则点O是△ABC的_____心PABCOEF内PA=PB=PCOA=OB=OCPE=PF=PGGOE=OF=OG3、已知三棱锥P-ABC的三条侧棱PA,PB,PC两两垂直,PO ⊥平面ABC,则点O是△ABC的_____心PABCDO垂四、针对性练习PABCODFAOD 例2、已知锐二面角?- l- ? ,A为面?内一点,A到? 的距离为 ,到 l 的距离为 4,求二面角 ?- l- ? 的大小。解:过 A作 AO⊥ ?于O,过 O作 OD⊥ l 于D,连AD∴AO= 2 ,AD=4∵ AO为 A到?的距离 , AD为 A到 l 的距离∴∠ADO就是二面角 ?- l- ? 的平面角∴ ∠ADO=60°∴二面角 ?- l- ? 的大小为60 °在R t △AOD中,∵sin∠ADO=
