2.2.2 椭圆的几何性质 课件(28张PPT)
文档属性
| 名称 | 2.2.2 椭圆的几何性质 课件(28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 734.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 19:42:34 | ||
图片预览






文档简介
课件28张PPT。椭圆的几何性质人教B版选修2-1第二章2.2.2焦点在 轴的椭圆的标准方程
话题:利用椭圆的标准方程来研究椭圆的
一些几何性质
问题1:我已经画出椭圆的图形,直接观察图形就可以得到椭圆的性质,为什么还要通过椭圆的方程研究椭圆的几何性质?
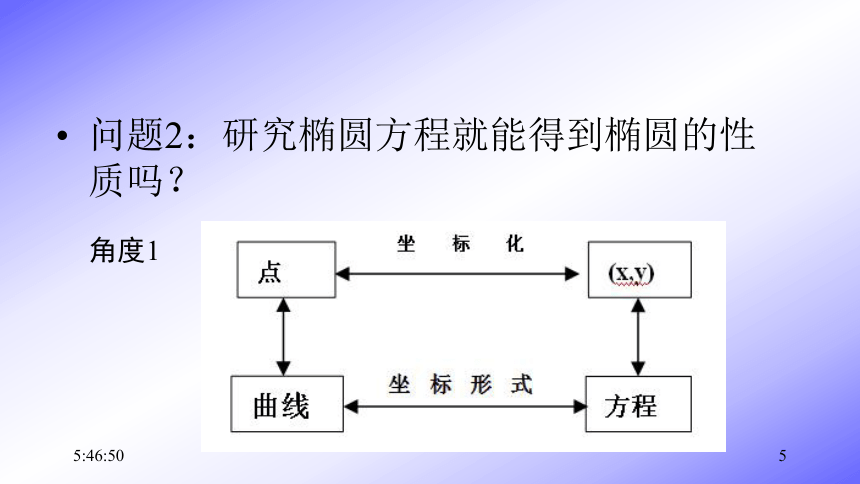
问题2:研究椭圆方程就能得到椭圆的性质吗?
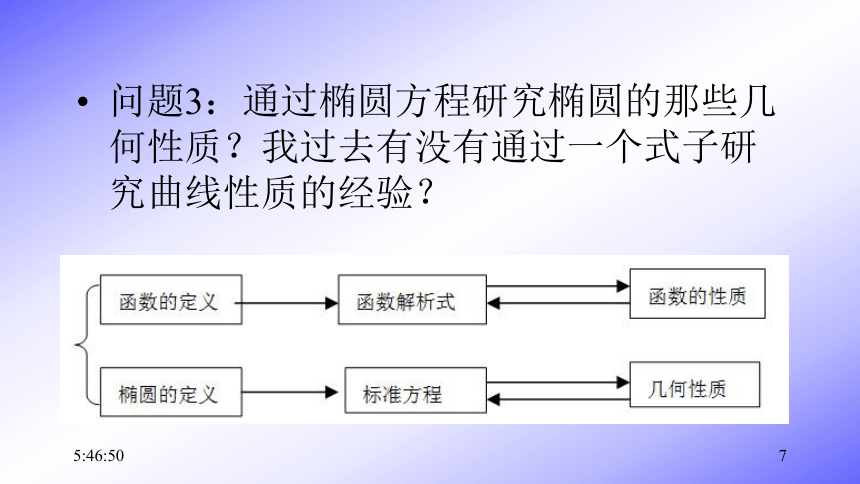
问题3:通过椭圆方程研究椭圆的那些几何性质?我过去有没有通过一个式子研究曲线性质的经验?
问题4:怎么研究方程得到几何性质?研究几何性质有什么用?
21:07:263存在问题,请你帮忙回答问题1:我已经画出椭圆的图形,直接观察图形就可以得到椭圆的性质,为什么还要通过椭圆的方程研究椭圆的几何性质?
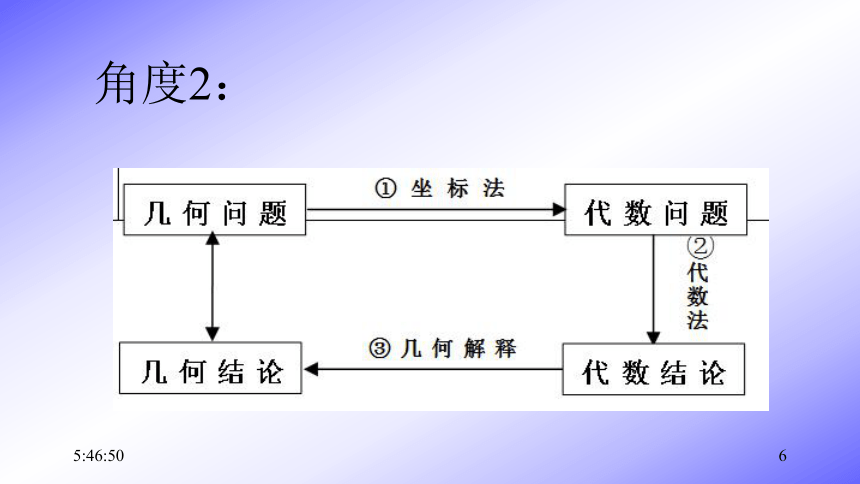
21:07:264有些曲线方程我们暂时画不出图像,比如曲线问题2:研究椭圆方程就能得到椭圆的性质吗?21:07:265角度1角度2:21:07:266问题3:通过椭圆方程研究椭圆的那些几何性质?我过去有没有通过一个式子研究曲线性质的经验?
21:07:267问题3:通过椭圆方程研究椭圆的那些几何性质?我过去有没有通过一个式子研究曲线性质的经验?
21:07:268通过方程研究椭圆的几何性质1.范围21:07:269函数定义域、值域通过方程研究椭圆的几何性质1.范围21:07:2610
椭圆落在 , 组成的矩形中研究范围的作用: 关于x轴对称关于y轴对称关于原点对称2.对称性3.顶点:
长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。a、b分别叫做椭圆的长半轴长和短半轴长。思考:曲线与坐标轴的交点是否就是曲线的顶点?举例说明。21:07:2714思考21:07:2715近地点(Perigee)是一个天文学上的用语,指航天器绕地球运行的椭圆轨道上距地心最近的一点。如果已知卫星运行的轨道方程为地心是运行轨道的一个焦点,求近地点到地心的距离.思考21:07:2717指数函数、对数函数因为底数不同有增减快慢的区别,所有椭圆形状一样吗?(1)4.离心率(2)(3)离心率:椭圆的焦距与长轴长的比叫做椭圆的离心率。21:07:2722基本元素1.基本量:a、b、c、e、(共四个量)2.基本点:顶点、焦点、中心(共七个点)3.基本线:对称轴(共两条线)基本量之间、基本点之间、基本线之间以及它们相互之间的关系(位置、数量之间的关系)例1 研究椭圆 的几何性质,并用描点法画出椭圆图形例2.已知曲线的方程是曲线上的点满足什么几何条件?有哪些几何性质?曲线卡西尼卵形线21:07:2727英国数学家詹姆斯?西尔维斯特:
“几何看来有时候要领先于分析,但事实上,
几何的先行于分析,只不过像一个仆人走在主人的前面一样,是为主人开路的”
作业21:07:2728
话题:利用椭圆的标准方程来研究椭圆的
一些几何性质
问题1:我已经画出椭圆的图形,直接观察图形就可以得到椭圆的性质,为什么还要通过椭圆的方程研究椭圆的几何性质?
问题2:研究椭圆方程就能得到椭圆的性质吗?
问题3:通过椭圆方程研究椭圆的那些几何性质?我过去有没有通过一个式子研究曲线性质的经验?
问题4:怎么研究方程得到几何性质?研究几何性质有什么用?
21:07:263存在问题,请你帮忙回答问题1:我已经画出椭圆的图形,直接观察图形就可以得到椭圆的性质,为什么还要通过椭圆的方程研究椭圆的几何性质?
21:07:264有些曲线方程我们暂时画不出图像,比如曲线问题2:研究椭圆方程就能得到椭圆的性质吗?21:07:265角度1角度2:21:07:266问题3:通过椭圆方程研究椭圆的那些几何性质?我过去有没有通过一个式子研究曲线性质的经验?
21:07:267问题3:通过椭圆方程研究椭圆的那些几何性质?我过去有没有通过一个式子研究曲线性质的经验?
21:07:268通过方程研究椭圆的几何性质1.范围21:07:269函数定义域、值域通过方程研究椭圆的几何性质1.范围21:07:2610
椭圆落在 , 组成的矩形中研究范围的作用: 关于x轴对称关于y轴对称关于原点对称2.对称性3.顶点:
长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。a、b分别叫做椭圆的长半轴长和短半轴长。思考:曲线与坐标轴的交点是否就是曲线的顶点?举例说明。21:07:2714思考21:07:2715近地点(Perigee)是一个天文学上的用语,指航天器绕地球运行的椭圆轨道上距地心最近的一点。如果已知卫星运行的轨道方程为地心是运行轨道的一个焦点,求近地点到地心的距离.思考21:07:2717指数函数、对数函数因为底数不同有增减快慢的区别,所有椭圆形状一样吗?(1)4.离心率(2)(3)离心率:椭圆的焦距与长轴长的比叫做椭圆的离心率。21:07:2722基本元素1.基本量:a、b、c、e、(共四个量)2.基本点:顶点、焦点、中心(共七个点)3.基本线:对称轴(共两条线)基本量之间、基本点之间、基本线之间以及它们相互之间的关系(位置、数量之间的关系)例1 研究椭圆 的几何性质,并用描点法画出椭圆图形例2.已知曲线的方程是曲线上的点满足什么几何条件?有哪些几何性质?曲线卡西尼卵形线21:07:2727英国数学家詹姆斯?西尔维斯特:
“几何看来有时候要领先于分析,但事实上,
几何的先行于分析,只不过像一个仆人走在主人的前面一样,是为主人开路的”
作业21:07:2728
