2.4.2 抛物线的几何性质 课件(26张PPT)
文档属性
| 名称 | 2.4.2 抛物线的几何性质 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 00:00:00 | ||
图片预览







文档简介
课件26张PPT。课程名称:抛物线的几何性质年 级:高 二教 材:人教B版 选修2-1课前任务 观看网上平台的 微课
并根据自主学习任务单
完成
1.导学案预习提纲
2.课前任务检测 抛物线y2=2px(p>0)的几何性质
1.范围
因为p>0,由方程y2=2px(p>0)可知,这条抛物线上任意一点M的坐标(x,y)满足不等式x≥0,所以这条抛物线在y轴的右侧;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸,它开口向右.
2.对称性
以-y代y,方程y2=2px(p>0)不变,因此这条抛物线是以x轴为对称轴的轴对称图形.抛物线的对称轴叫做抛物线的轴.
3.顶点
抛物线和它的轴的交点叫做抛物线的顶点,在方程y2=2px(p>0)中,当y=0时,x=0,因此这条抛物线的顶点就是坐标原点.4.离心率
抛物线上的点到焦点和准线的距离的比,叫做抛物线的离心率,
用e表示.按照抛物线的定义,e=1. (1)抛物线只位于 个坐标平面内,它可以无限延伸,
但没有渐近线; (2)抛物线只有 条对称轴,
对称中心;(3)抛物线只有 个顶点、
个焦点、 条准线 (4)抛物线的离心率是确定的,
其值为 .半1无1 111抛物线几何性质的特点:课前任务总结课前任务总结课前任务完善—组内互助任务: 1.归纳并对比四种方程所表示的抛物线
的几何性质的异同
2.完善课前检测的做题步骤,以小组
为单位上传。
时间:5分钟
要求:第4分钟时,老师将随意指派每组上传
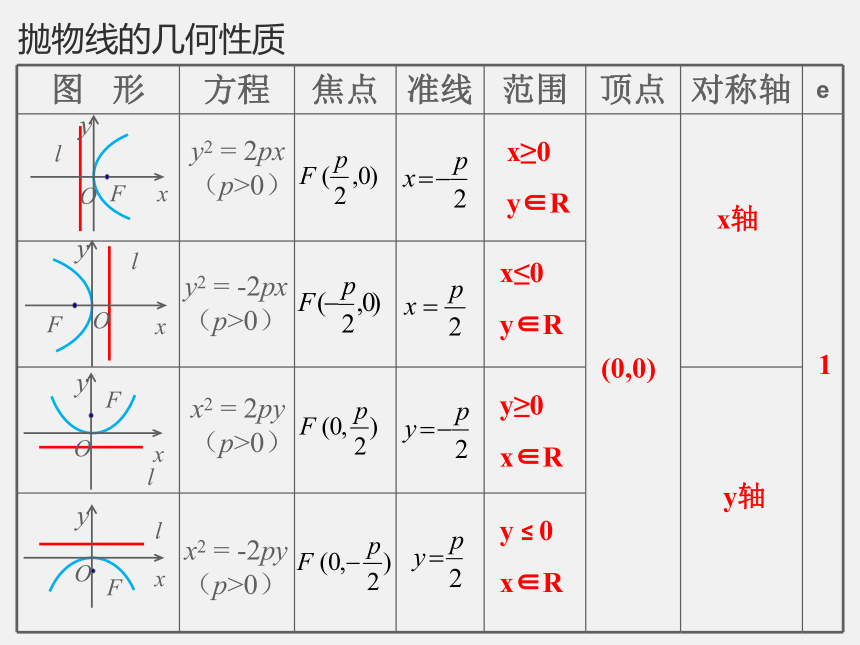
的内容。 抛物线的几何性质y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)x≥0
y∈Rx≤0
y∈Ry≥0
x∈Ry ≤ 0
x∈R(0,0)x轴y轴1归纳总结:对称轴要看一次项,符号确定开口方向,
如果y是一次项,y的系数为负时开口向下,y的系数
为正时开口向上.如果x是一次项,x的系数为负时开
口向左,x的系数为正时开口向右.四种位置的抛物线几何性质的对比
共同点:
①原点在抛物线上;
②焦点在坐标轴上;
③焦点的非零坐标都是一次项系数的1/4 .
不同点:
①焦点在x轴上时,方程的右端为±2px,左端为y2;焦点在y轴上时,方程的 右端为±2py,左端为x2;
②开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)正半轴上,方程右 端取正号;
开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)负半轴上,方程右端取负号.开口向右开口向左开口向上开口向下 抢答:填空(顶点在原点,焦点在坐标轴上) 课前检测第3题: 汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯泡位于抛物线焦点处。已知灯口的直24cm,灯深10cm,那么灯泡与反射镜的顶点(即截得抛物线的顶点)距离是多少?(10,12)所在平面内建立直
角坐标系,使反射镜
的顶点与原点重合,
x轴垂直于灯口直径.取反射镜的轴即抛物线
的轴为x轴,抛物线
的顶点为坐标原点,
建立平面直角
坐标系xoy,如图所示:设抛物线的方程为:y2=2px (p>0),由条件可得A (10,12),代入方程得:122=2p·10,解得: p=抛物线焦点F的坐标为(3.6,0).解:因此灯泡与反射镜顶点的距离是3.6cm题型一题型二题型三根据抛物线的标准方程研究几何性质
【例1】 已知抛物线的标准方程如下,分别求出它们的焦点坐标和准线方程.
(1)x2=-8y; (2)2y2+7x=0.
分析:先把所给方程化为标准方程,求出p,再根据开口方向,写出焦点坐标和准线方程.
解:(1)由抛物线的标准方程知抛物线的焦点在y轴的负半轴上,开口向下.∵p=4,∴焦点坐标为(0,-2),准线方程为y=2.典型例题:?题型一题型二题型三典型例题:题型一题型二题型三?根据抛物线的几何性质求标准方程典型例题:? 反思:求抛物线方程常用待定系数法,当抛物线类型不确定时,要注意讨论题型一题型二题型三典型例题:题型一题型二题型三抛物线几何性质的实际应用
【例3】 探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口圆的直径为60 cm,灯深为40 cm,求抛物线的标准方程和焦点坐标.
分析:建立适当的坐标系确定抛物线上一点的坐标,从而确定焦参数p,求得其方程.典型例题:? 反思:解决本题的关键是建立适当的坐标系,求出抛物线的标准方程,进而求出焦点坐标.题型一题型二题型三典型例题:课堂巩固:1. 抛物线的几何性质: 范围、对称性、顶点、离心率;
2.三种题型:
(1)利用抛物线的标准方程研究几何性质;
(2)利用抛物线的几何性质求标准方程;
(3)抛物线几何性质的实际应用。小 结:分层作业:A层 P65 习题B 1、2、3、4
B层 P64 练习B 1、2、3
C层 P63 练习A 1、2、3合作探究:8 谢谢大家~
并根据自主学习任务单
完成
1.导学案预习提纲
2.课前任务检测 抛物线y2=2px(p>0)的几何性质
1.范围
因为p>0,由方程y2=2px(p>0)可知,这条抛物线上任意一点M的坐标(x,y)满足不等式x≥0,所以这条抛物线在y轴的右侧;当x的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸,它开口向右.
2.对称性
以-y代y,方程y2=2px(p>0)不变,因此这条抛物线是以x轴为对称轴的轴对称图形.抛物线的对称轴叫做抛物线的轴.
3.顶点
抛物线和它的轴的交点叫做抛物线的顶点,在方程y2=2px(p>0)中,当y=0时,x=0,因此这条抛物线的顶点就是坐标原点.4.离心率
抛物线上的点到焦点和准线的距离的比,叫做抛物线的离心率,
用e表示.按照抛物线的定义,e=1. (1)抛物线只位于 个坐标平面内,它可以无限延伸,
但没有渐近线; (2)抛物线只有 条对称轴,
对称中心;(3)抛物线只有 个顶点、
个焦点、 条准线 (4)抛物线的离心率是确定的,
其值为 .半1无1 111抛物线几何性质的特点:课前任务总结课前任务总结课前任务完善—组内互助任务: 1.归纳并对比四种方程所表示的抛物线
的几何性质的异同
2.完善课前检测的做题步骤,以小组
为单位上传。
时间:5分钟
要求:第4分钟时,老师将随意指派每组上传
的内容。 抛物线的几何性质y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)x≥0
y∈Rx≤0
y∈Ry≥0
x∈Ry ≤ 0
x∈R(0,0)x轴y轴1归纳总结:对称轴要看一次项,符号确定开口方向,
如果y是一次项,y的系数为负时开口向下,y的系数
为正时开口向上.如果x是一次项,x的系数为负时开
口向左,x的系数为正时开口向右.四种位置的抛物线几何性质的对比
共同点:
①原点在抛物线上;
②焦点在坐标轴上;
③焦点的非零坐标都是一次项系数的1/4 .
不同点:
①焦点在x轴上时,方程的右端为±2px,左端为y2;焦点在y轴上时,方程的 右端为±2py,左端为x2;
②开口方向与x轴(或y轴)的正半轴相同,焦点在x轴(或y轴)正半轴上,方程右 端取正号;
开口方向与x轴(或y轴)的负半轴相同,焦点在x轴(或y轴)负半轴上,方程右端取负号.开口向右开口向左开口向上开口向下 抢答:填空(顶点在原点,焦点在坐标轴上) 课前检测第3题: 汽车前灯反射镜与轴截面的交线是抛物线的一部分,灯泡位于抛物线焦点处。已知灯口的直24cm,灯深10cm,那么灯泡与反射镜的顶点(即截得抛物线的顶点)距离是多少?(10,12)所在平面内建立直
角坐标系,使反射镜
的顶点与原点重合,
x轴垂直于灯口直径.取反射镜的轴即抛物线
的轴为x轴,抛物线
的顶点为坐标原点,
建立平面直角
坐标系xoy,如图所示:设抛物线的方程为:y2=2px (p>0),由条件可得A (10,12),代入方程得:122=2p·10,解得: p=抛物线焦点F的坐标为(3.6,0).解:因此灯泡与反射镜顶点的距离是3.6cm题型一题型二题型三根据抛物线的标准方程研究几何性质
【例1】 已知抛物线的标准方程如下,分别求出它们的焦点坐标和准线方程.
(1)x2=-8y; (2)2y2+7x=0.
分析:先把所给方程化为标准方程,求出p,再根据开口方向,写出焦点坐标和准线方程.
解:(1)由抛物线的标准方程知抛物线的焦点在y轴的负半轴上,开口向下.∵p=4,∴焦点坐标为(0,-2),准线方程为y=2.典型例题:?题型一题型二题型三典型例题:题型一题型二题型三?根据抛物线的几何性质求标准方程典型例题:? 反思:求抛物线方程常用待定系数法,当抛物线类型不确定时,要注意讨论题型一题型二题型三典型例题:题型一题型二题型三抛物线几何性质的实际应用
【例3】 探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口圆的直径为60 cm,灯深为40 cm,求抛物线的标准方程和焦点坐标.
分析:建立适当的坐标系确定抛物线上一点的坐标,从而确定焦参数p,求得其方程.典型例题:? 反思:解决本题的关键是建立适当的坐标系,求出抛物线的标准方程,进而求出焦点坐标.题型一题型二题型三典型例题:课堂巩固:1. 抛物线的几何性质: 范围、对称性、顶点、离心率;
2.三种题型:
(1)利用抛物线的标准方程研究几何性质;
(2)利用抛物线的几何性质求标准方程;
(3)抛物线几何性质的实际应用。小 结:分层作业:A层 P65 习题B 1、2、3、4
B层 P64 练习B 1、2、3
C层 P63 练习A 1、2、3合作探究:8 谢谢大家~
