3.2.4 二面角及其度量 课件(17张PPT)
文档属性
| 名称 | 3.2.4 二面角及其度量 课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 19:43:45 | ||
图片预览




文档简介
课件17张PPT。 求二面角一:复习回顾1 二面角及其平面角的定义。
2 二面角的几种求法。
(一)定义法定义法:在二面角的棱上取一个特殊点,由此点出发在二面角的两个面内分别作棱的垂线;
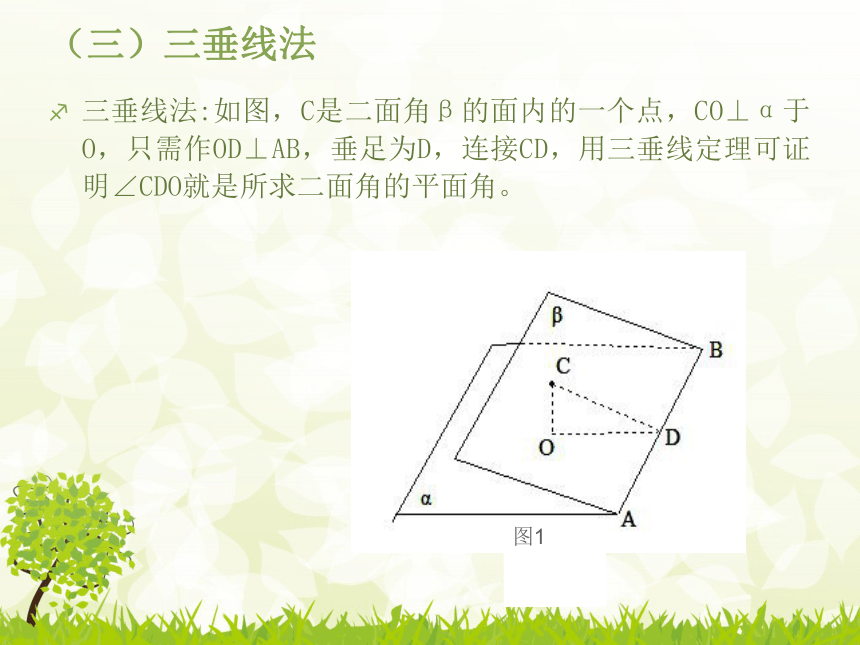
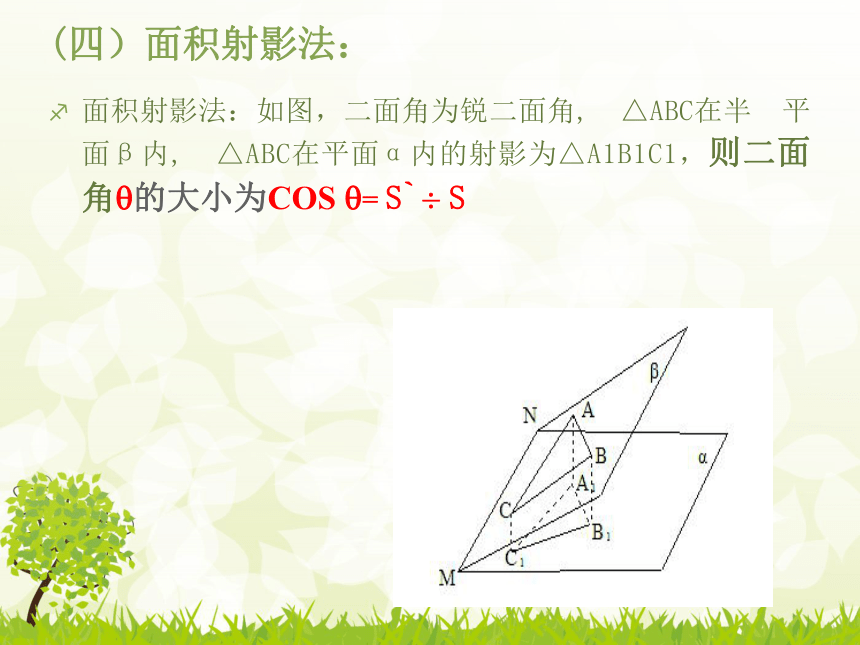
ABβpια(二)垂面法垂面法:即在二面角的棱上取一点,过此点作平面,使垂直于二面角的棱,则 与二面角的两个面的交线所成的角就是该二面角的平面角。(三)三垂线法三垂线法:如图,C是二面角β的面内的一个点,CO⊥α于O,只需作OD⊥AB,垂足为D,连接CD,用三垂线定理可证明∠CDO就是所求二面角的平面角。(四)面积射影法:面积射影法:如图,二面角为锐二面角, △ABC在半 平面β内, △ABC在平面α内的射影为△A1B1C1,则二面角?的大小为COS ?= S`÷ S(五)空间向量法空间向量法:建立空间直角坐标系,求出两平面的法向量,利用向量的夹角公式进行计算。
(六)无棱找棱法无棱找棱法:当二面角无棱时,可以找出棱,在用其他方法求出其二面角。 二 典例分析1.如图,在正方体AC1中
(1)E为D1C1中点,则二面角E-BD-C的一个平面角为————
(2)求平面ADD1与平面D1BC所成锐二面角。
定义法CD
p垂面法DABB1E三垂线法DBFCAA1B1C1D1P典例分析2 如图,已知AB面ACD,DE面ACD,ACD为等边三角形,AD=DE=2AB,F为CD的中点,(Ⅰ)求证:AF // 面BCE;(Ⅱ)求二面角A-CE-D的正切值.
典例分析 3 如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交与点D
(1)求证:BD⊥平面AA1C1C。
(2) 求二面角C1-AB-C的余弦值。典例分析4 在等腰三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点, ,O为BC的中点,将三角形ADE沿DE折起,得到如图所示的四棱锥A1-BCDE,其中
(1)求证A1O⊥平面BCDE
(2)求二面角A1-CD-B的平面角的余弦值。典例分析5 已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形(1)证明BN⊥平面C1B1N(2求二面角的 正弦值。三 课堂小结(一)求二面角的六种方法。
1 定义法
2 垂面法
3 三垂线法
4 射影面积法
5 空间向量法
6 无棱找棱法
(二)二面角的计算
一“作”二“证”三“计算”
四 课后巩固1.如图,将边长为2的正方形ABCD沿对角线BD 折成一个直二面角,且EA⊥平面ABD,AE= ,(Ⅰ)若 ,求证:AB∥平面CDE;(Ⅱ)求实数的值,使得二面角A-EC-D的大小为60°.
再见
2 二面角的几种求法。
(一)定义法定义法:在二面角的棱上取一个特殊点,由此点出发在二面角的两个面内分别作棱的垂线;
ABβpια(二)垂面法垂面法:即在二面角的棱上取一点,过此点作平面,使垂直于二面角的棱,则 与二面角的两个面的交线所成的角就是该二面角的平面角。(三)三垂线法三垂线法:如图,C是二面角β的面内的一个点,CO⊥α于O,只需作OD⊥AB,垂足为D,连接CD,用三垂线定理可证明∠CDO就是所求二面角的平面角。(四)面积射影法:面积射影法:如图,二面角为锐二面角, △ABC在半 平面β内, △ABC在平面α内的射影为△A1B1C1,则二面角?的大小为COS ?= S`÷ S(五)空间向量法空间向量法:建立空间直角坐标系,求出两平面的法向量,利用向量的夹角公式进行计算。
(六)无棱找棱法无棱找棱法:当二面角无棱时,可以找出棱,在用其他方法求出其二面角。 二 典例分析1.如图,在正方体AC1中
(1)E为D1C1中点,则二面角E-BD-C的一个平面角为————
(2)求平面ADD1与平面D1BC所成锐二面角。
定义法CD
p垂面法DABB1E三垂线法DBFCAA1B1C1D1P典例分析2 如图,已知AB面ACD,DE面ACD,ACD为等边三角形,AD=DE=2AB,F为CD的中点,(Ⅰ)求证:AF // 面BCE;(Ⅱ)求二面角A-CE-D的正切值.
典例分析 3 如图,三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交与点D
(1)求证:BD⊥平面AA1C1C。
(2) 求二面角C1-AB-C的余弦值。典例分析4 在等腰三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点, ,O为BC的中点,将三角形ADE沿DE折起,得到如图所示的四棱锥A1-BCDE,其中
(1)求证A1O⊥平面BCDE
(2)求二面角A1-CD-B的平面角的余弦值。典例分析5 已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形(1)证明BN⊥平面C1B1N(2求二面角的 正弦值。三 课堂小结(一)求二面角的六种方法。
1 定义法
2 垂面法
3 三垂线法
4 射影面积法
5 空间向量法
6 无棱找棱法
(二)二面角的计算
一“作”二“证”三“计算”
四 课后巩固1.如图,将边长为2的正方形ABCD沿对角线BD 折成一个直二面角,且EA⊥平面ABD,AE= ,(Ⅰ)若 ,求证:AB∥平面CDE;(Ⅱ)求实数的值,使得二面角A-EC-D的大小为60°.
再见
