2.3.2 双曲线的几何性质(二) 课件(18张PPT)
文档属性
| 名称 | 2.3.2 双曲线的几何性质(二) 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-25 00:00:00 | ||
图片预览




文档简介
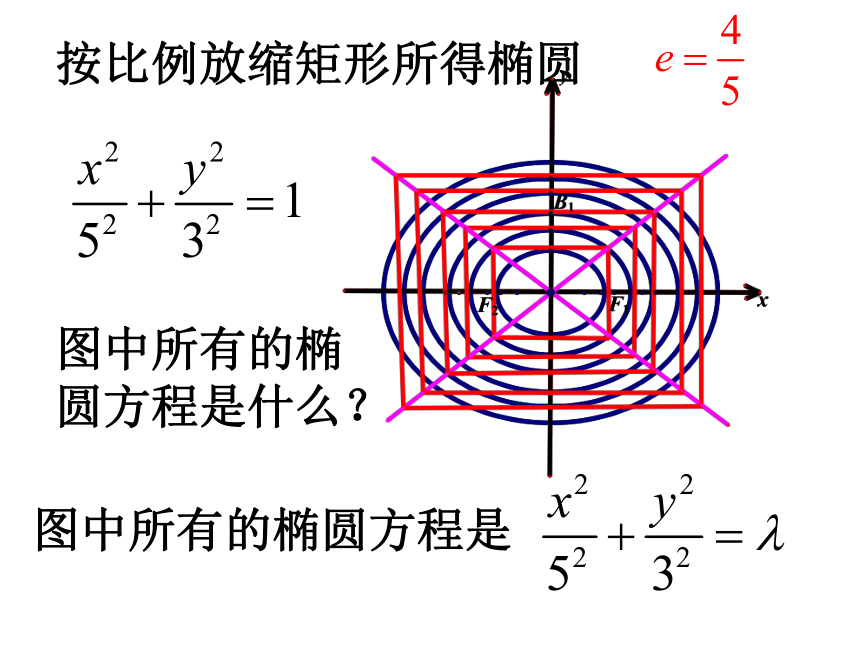
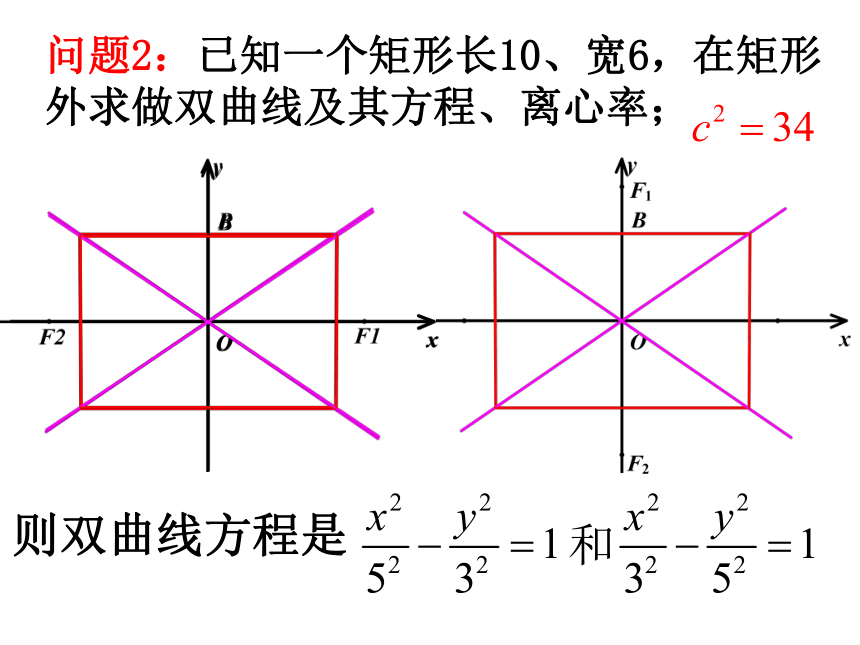
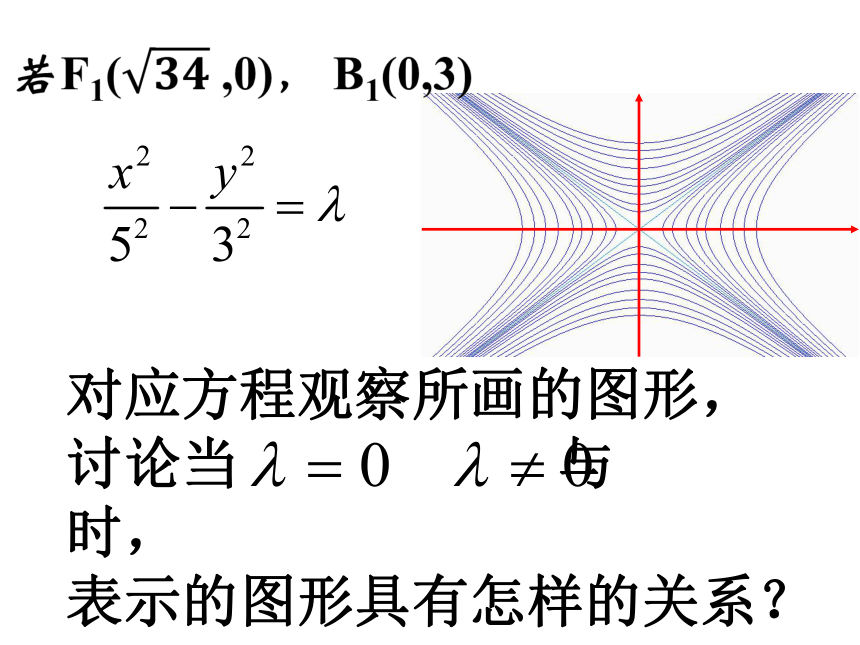
课件18张PPT。双曲线的几何性质(2)问题1:已知一个矩形长10、宽6,在矩形内求做一个椭圆及其方程、离心率;则椭圆方程是按比例放缩矩形所得椭圆图中所有的椭圆方程是图中所有的椭圆方程是什么?问题2:已知一个矩形长10、宽6,在矩形外求做双曲线及其方程、离心率;则双曲线方程是和写出所有双曲线的方程??对应方程观察所画的图形,
讨论当 与 时,
表示的图形具有怎样的关系??总结1:共同渐近线的双曲线系与双曲线有相同渐近线的双曲线方程可设为 形如 的双曲线渐近线方
程可设为(1)求与双曲线 有共同的 渐近线,且过点 的双曲线方 程是 。有效使用此双曲线系(2)已知双曲线的渐近线方程是
,求双曲线的离心率. 观察这两个离心率,能发现怎样的关系式?总结2:具有共同渐近线的双曲线系拥有两类双曲线,他们具有形似特征,其离心率的关系式:(2)已知双曲线的渐近线方程是
,求双曲线的离心率. 再观察这两个离心率,与渐近线之间的夹角有什么关系?总结3:双曲线渐近线夹角为 ,则的或问题3:方程与椭圆有什么关系?方程与双曲线有什么关系?有共同焦点空间直角坐标系中提升维度的思考:椭圆柱面椭圆抛物面空间直角坐标系中与提升维度的思考:椭圆抛物面平面直角坐标系中空间直角坐标系中与提升维度的思考:双曲抛物面(马鞍面)马鞍面在等高处的投影小结:
对曲线系方程中含有参数的研究:(1)双曲线的渐近线相同;
(2)双曲线的离心率相同;
(3)双曲线的焦点相同;
(4)升高维度再认识曲线与方程。
讨论当 与 时,
表示的图形具有怎样的关系??总结1:共同渐近线的双曲线系与双曲线有相同渐近线的双曲线方程可设为 形如 的双曲线渐近线方
程可设为(1)求与双曲线 有共同的 渐近线,且过点 的双曲线方 程是 。有效使用此双曲线系(2)已知双曲线的渐近线方程是
,求双曲线的离心率. 观察这两个离心率,能发现怎样的关系式?总结2:具有共同渐近线的双曲线系拥有两类双曲线,他们具有形似特征,其离心率的关系式:(2)已知双曲线的渐近线方程是
,求双曲线的离心率. 再观察这两个离心率,与渐近线之间的夹角有什么关系?总结3:双曲线渐近线夹角为 ,则的或问题3:方程与椭圆有什么关系?方程与双曲线有什么关系?有共同焦点空间直角坐标系中提升维度的思考:椭圆柱面椭圆抛物面空间直角坐标系中与提升维度的思考:椭圆抛物面平面直角坐标系中空间直角坐标系中与提升维度的思考:双曲抛物面(马鞍面)马鞍面在等高处的投影小结:
对曲线系方程中含有参数的研究:(1)双曲线的渐近线相同;
(2)双曲线的离心率相同;
(3)双曲线的焦点相同;
(4)升高维度再认识曲线与方程。
