湘教数学八下2.2.2平行四边形的判定定理(2) 课件(12张PPT)
文档属性
| 名称 | 湘教数学八下2.2.2平行四边形的判定定理(2) 课件(12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 306.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-07-27 00:00:00 | ||
图片预览




文档简介
课件12张PPT。 实验室有一块平行四边形的玻璃片(记作:□ABCD),在做实验时,小明不小心碰碎了一部分(如图所示),他想配一块一模一样的赔给学校,如果把剩下的玻璃带去玻璃店,他能配到吗?生活实际的挑战2.2.2 平行四边形的判定(2)
学习目标:
1、理解并掌握“对角线互相平分的四边形是平行四边形和两组对角分别相等的四边形是平行四边形”这两个判定方法。
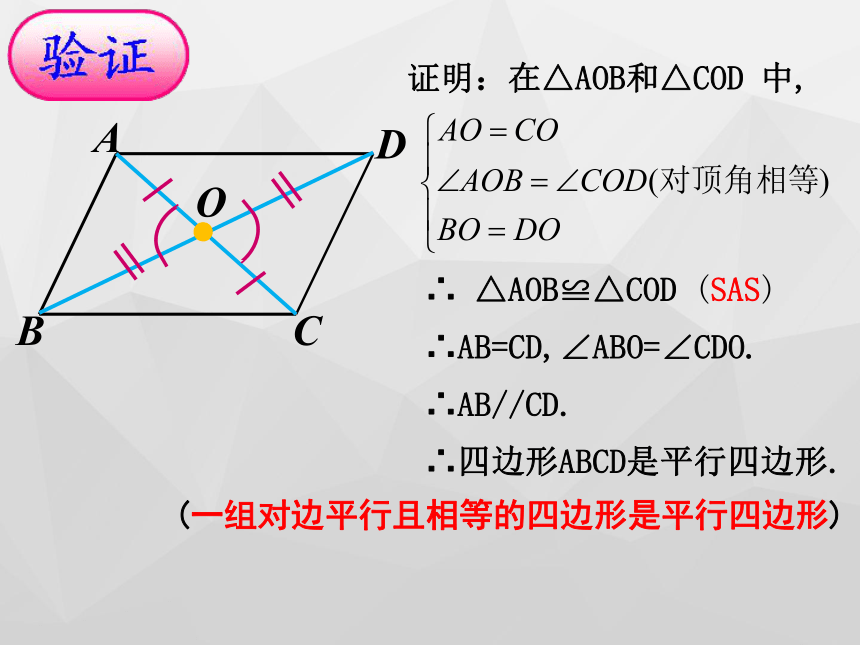
2、会运用平行四边形的判定定理判定一个四边形是否为平行四边形。 证明:在△AOB和△COD 中,∴ △AOB≌△COD (SAS)∴AB=CD,∠ABO=∠CDO. ∴AB//CD. ∴四边形ABCD是平行四边形. (一组对边平行且相等的四边形是平行四边形)∵OA=OC,OB=OD.
∴四边形ABCD是平行四边形.
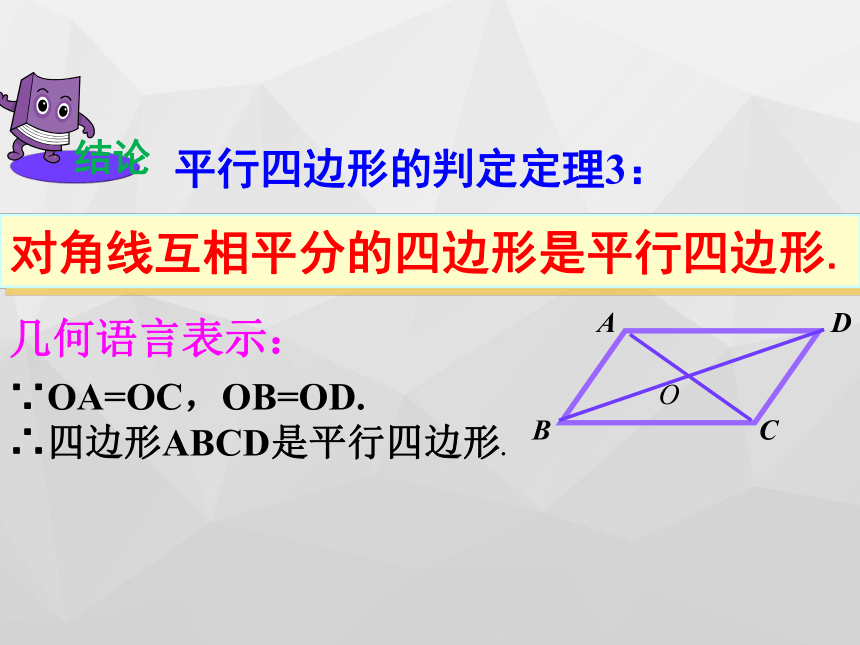
几何语言表示:平行四边形的判定定理3:对角线互相平分的四边形是平行四边形. 已知:如图, ABCD的对角线AC, BD相交于点O,点E、F在BD上,且OE=OF. 求证:四边形AECF也是平行四边形.证明:
∵四边形ABCD是平行四边形
∴OA=OC.
又∵OE=OF,
∴四边形AECF是平行四边形.(对角线互相平分的四边形是平行四边形) 已知:如图,在四边形ABCD中∠A= ∠ C, ∠ B= ∠ D 求证:四边形ABCD是平行四边形.
证明:∵ ∠A= ∠ C, ∠ B= ∠ D,
∠A+∠ B+∠ C+∠ D=360°,
∴ 2(∠A+∠ B)=360°
∴ ∠A+∠ B=180°
∴AD//BC
同理可证:AB//DC,
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)∵∠A=∠C,∠B=∠D.
∴四边形ABCD是平行四边形.
几何语言表示:平行四边形的判定定理4:两组对角分别相等的四边形是平行四边形. 请你识别下列四边形是否是平行四边形?请说明理由?能,一组对边平行且相等。能,两组对角分别相等。能,两组对边分别相等。能,对角线互相平分。1.两组邻边分别相等的四边形一定是平行四边形吗?如果是,请说明理由;如果不是,请举出反例.2.一组对边相等,另一组对边平行的四边形一定是平行四边形吗?如果是,请说明理由;如果不是,请举出反例.解:不一定是平行四边形,如筝形:解:不一定是平行四边形,如等腰梯形: 已知:如图, 把△ ABC的中线AD延长到 E,使得DE=AD,连接EB,EC.
求证:四边形ABEC是平行四边形. 如图,平行四边形ABCD的对角线相交于点O,直线MN经过点O,分别与AB,CD交于点M,N,连接AN,CM.
求证:四边形AMCN是平行四边形.本节课你有哪些收获?
五种判定方法(定义、4个判定定理)
数形结合的数学思想
一题多解的数学方法
1、理解并掌握“对角线互相平分的四边形是平行四边形和两组对角分别相等的四边形是平行四边形”这两个判定方法。
2、会运用平行四边形的判定定理判定一个四边形是否为平行四边形。 证明:在△AOB和△COD 中,∴ △AOB≌△COD (SAS)∴AB=CD,∠ABO=∠CDO. ∴AB//CD. ∴四边形ABCD是平行四边形. (一组对边平行且相等的四边形是平行四边形)∵OA=OC,OB=OD.
∴四边形ABCD是平行四边形.
几何语言表示:平行四边形的判定定理3:对角线互相平分的四边形是平行四边形. 已知:如图, ABCD的对角线AC, BD相交于点O,点E、F在BD上,且OE=OF. 求证:四边形AECF也是平行四边形.证明:
∵四边形ABCD是平行四边形
∴OA=OC.
又∵OE=OF,
∴四边形AECF是平行四边形.(对角线互相平分的四边形是平行四边形) 已知:如图,在四边形ABCD中∠A= ∠ C, ∠ B= ∠ D 求证:四边形ABCD是平行四边形.
证明:∵ ∠A= ∠ C, ∠ B= ∠ D,
∠A+∠ B+∠ C+∠ D=360°,
∴ 2(∠A+∠ B)=360°
∴ ∠A+∠ B=180°
∴AD//BC
同理可证:AB//DC,
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)∵∠A=∠C,∠B=∠D.
∴四边形ABCD是平行四边形.
几何语言表示:平行四边形的判定定理4:两组对角分别相等的四边形是平行四边形. 请你识别下列四边形是否是平行四边形?请说明理由?能,一组对边平行且相等。能,两组对角分别相等。能,两组对边分别相等。能,对角线互相平分。1.两组邻边分别相等的四边形一定是平行四边形吗?如果是,请说明理由;如果不是,请举出反例.2.一组对边相等,另一组对边平行的四边形一定是平行四边形吗?如果是,请说明理由;如果不是,请举出反例.解:不一定是平行四边形,如筝形:解:不一定是平行四边形,如等腰梯形: 已知:如图, 把△ ABC的中线AD延长到 E,使得DE=AD,连接EB,EC.
求证:四边形ABEC是平行四边形. 如图,平行四边形ABCD的对角线相交于点O,直线MN经过点O,分别与AB,CD交于点M,N,连接AN,CM.
求证:四边形AMCN是平行四边形.本节课你有哪些收获?
五种判定方法(定义、4个判定定理)
数形结合的数学思想
一题多解的数学方法
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
